1 курс / ОТК 1 курс-20191213T204228Z-001 / ОТК / Л_тература по ОТК / otksp_STZI_press для диска

1.За однакової конфігурації схеми порядок диференціального рівняння кола з нелінійними елементами буде такий самий, як і лінійного кола (вище визначалися рівняння другого порядку).

2.Диференціальне рівняння можна записати у двох формах – за допомогою нелінійних характеристик (2.49) – (2.51) або через динамічні параметри.

3.Нелінійні коефіцієнти диференціального рівняння залежать від того, який аналітичний вигляд мають характеристики нелінійних елементів.

2.9.4 Нелінійні резистивні кола постійного струму

Принципи аналізу стаціонарного режиму нелінійного кола постійного струму доцільно розглянути на прикладі простих схем з послідовним (рис.2.41, а) та паралельним (рис.2.41, б) з’єднанням нелінійних опорів.

Рисунок 2.41 – Нелінійні резистивні кола

Напруги та струми позначено в даному підрозділі малими літерами, оскільки цей матеріал справедливий не тільки для постійного струму, але й для миттєвих значень змінного струму.

Нехай відомо значення ЕРС e та ВАХ нелінійних опорів (рис.2.42, а):

диться до розв’язання нелінійного диференціального рівняння. Крім того, як правило, точні аналітичні вирази ВАХ нелінійних опорів невідомі, а тільки апроксимуються з деякою точністю.

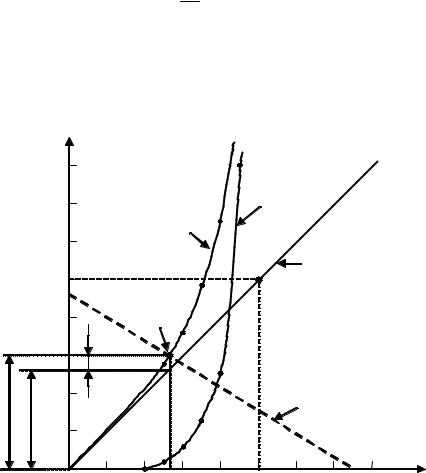
Рисунок 2.42 – Графічний розрахунок кола послідовно з’єднаних нелінійних опорів

Якщо ВАХ елементів задано графічно (рис.2.42, а), режим кола розраховують у такий спосіб. Обидві характеристики будують в одній системі координат (i, u) , але для однієї ВАХ i = ϕ1(u) початком координат є точка 0 і напругу

відкладають вправо від цієї точки. Для іншої ВАХ i = ϕ2 (u) початком коорди-

нат є точка 0′ осі абсцис, де u = e , і значення напруг відкладають вліво від цієї точки (рис.2.42, б). Криві перетинаються в точці m , яка і визначає режим кола.

Дійсно, в цій точці струм i0 , спільний для двох опорів, задовольняє рівнянням (2.62) і (2.63), а напруги u1(i0 ) та u2 (i0 ) − рівнянню (2.64).

Для окремого випадку, коли один з опорів, наприклад R2 , лінійний, його

ВАХ будують як пряму (на рис.2.42, б позначена пунктиром), проведену з точки 0′ під кутом, пропорційним опору R2 .

Зазначимо, що струм i0 можна знайти інакше, підсумовуючи, згідно з рівністю (2.64), величини u1 та u2 при кожному значенні струму i , тобто додаючи графіки i = ϕ1(u) та i = ϕ2 (u) за напругою. Точка m1 перетину сумарної ВАХ i = ϕ0 (u) з вертикаллю, проведеною з точки e на осі абсцис, і визначатиме шуканий струм i0 (рис.2.42, а).

Аналогічно розв’язують задачу розрахунку паралельного кола (рис.2.41, б). Згідно з першим законом Кірхгофа i0 = i1 +i2 .

Якщо заданий загальний струм i0 , а слід знайти загальну напругу u0 і струми віток i1 та i2 , на одному графіку будують ВАХ елементів u = f1(i) та u = f2 (i) , причому для однієї з характеристик початком координат є точка i = i0 (рис.2.43, а). Точка n перетину двох ВАХ визначає величини u0 , i1, i2 .

Якщо задано напругу u0 , доцільніше побудувати характеристики (рис.2.43, б) i = ϕ1(u) та i = ϕ2 (u) . Ординати цих ВАХ для заданого значення u0 визначають струми i1(u0 ) та i2 (u0 ) , а сума цих ординат – загальний струм i0 . На рис.2.43, б сумарну ВАХ позначено i = ϕ0 (u) .

наведена в табл.2.3. Розрахувати струми усіх віток графічним методом.

Таблиця 2.3 – ВАХ нелінійного елемента

Рисунок 2.44 – Схеми нелінійних кіл з мішаним і послідовним з’єднанням опорів

Розв’язання.

1.Будуємо ВАХ нелінійного опору i3 (u) за даними табл.2.3 і ВАХ лінійного опору i2 (u) =u / R2 (рис.2.45). Пряма i2 (u) проходить через початок координат. Другу точку для її побудови візьмемо таку: i2 (1) =1/ 20 = 0,05 А.

2.Підсумовуючи ці характеристики, знаходимо i23 (u) − ВАХ еквівалентного нелінійного опору, утвореного лінійним опором R2 та нелінійним R3 (i) .

3. Будуємо ВАХ i1(u) лінійного опору R1 як пряму (на рис.2.45 позначена пунктиром), проведену з точки u = E під кутом, пропорційним опору R2 , причому значення напруг відкладаємо вліво від цієї точки. Рівняння цієї ВАХ має вигляд:

i1(u) = − 1 (u − E) = E −u .

R1 R1

Щоб побудувати цю пряму, знайдемо значення i1(0) = (1,5 −0) / 33 = 0,0454 А. 4. ВАХ i1(u) та i23 (u) перетинаються в точці m , котра і визначає режим кола:

U23 ≈ 0,53В; I1 ≈ 30 мА; I2 ≈ 27 мА; I3 ≈ 3 мА.

Рисунок 2.45 – Графічний розрахунок кола у прикладі 2.11

2.10 Основи матрично-топологічного методу аналізу кіл

Реальні електричні кола з урахуванням різних режимів їхньої роботи описують сотнями і тисячами рівнянь стану. При цьому втрачається наочність складання системи такої великої кількості рівнянь. Усувається цей недолік шляхом подання системи рівнянь у матричній формі. Процедура запису матричних рівнянь значно спрощується, якщо розглядати замість схем їхню топологію (графи схем). Такий підхід до аналізу електричних схем називають матрич- но-топологічним методом.

2.10.1 Топологія електричних схем

Загальний метод складання лінійно-незалежних рівнянь кола можна одержати, використовуючи поняття теорії лінійних графів, одного з розділів математичної дисципліни – топології.

До лінійного графа приводять наступні міркування: рівняння рівноваги струмів і напруг, складені за законами Кірхгофа, визначаються тільки геометричною структурою кола і не залежать від фізичного змісту віток. Тому при складанні рівнянь з’єднань зручно абстрагуватись від виду і характеристик віток, замінивши їх відрізками ліній.

В результаті для схеми, що містить довільні двополюсні елементи, одержують лінійний граф як сукупність двох елементів – вузлів (вершин) і віток (ребер), що зображають відрізками ліній, які з’єднують пари вузлів.

Треба зазначити, що на топологічній схемі джерела напруги і струму не зображають. При цьому вітка з джерелом ЕРС зберігається, вітки з ідеальними джерелами струму взагалі в топологічну схему не входять, бо внутрішня провідність таких джерел дорівнює нулю і відповідно внутрішній опір дорівнює нескінченності.

Як і задана схема, її граф може мати різну структуру. Розрізняють планарний (плаский) граф, якщо його можна зобразити на площині без перетину віток і непланарний (просторовий) граф, якщо його неможливо зобразити на площині без перетину віток.

Граф, довільну пару вершин якого з’єднує вітка або сукупність віток, нази-

вають зв’язним.

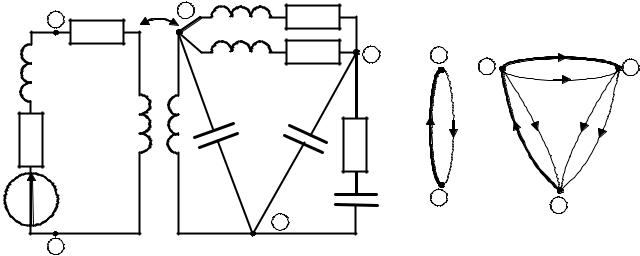
Якщо на графі вказані умовно-додатні напрямки струмів або напруг, такий граф називають направленим графом схеми. Направлений граф схеми (рис.2.46,а) зображений на рис.2.46,б (номери вузлів позначено кружками).

Рисунок 2.46 – Схема (а) та її граф (б)

Слід відмітити, що внаслідок особливості врахування ЕРС взаємної індукції граф схеми (рис.2.46, а) поділяється на дві окремі, не зв’язані частини, тобто є незв’язаним планарним графом.

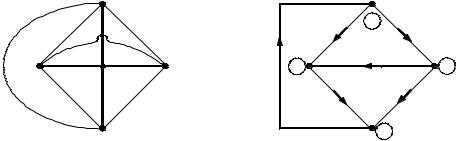
Приклад непланарного графа показаний на рис.2.47, а.

Важливим топологічним поняттям графа схеми є дерево графа – довільна сукупність віток графа, які з’єднують всі вузли графа без утворення контурів. Видалені з графа при утворенні дерева вітки називають головними вітками графа, або вітками зв’язку. Очевидно, кількість віток довільного дерева на одиницю менша кількості вузлів, тобто дорівнює n −1, а кількість віток зв’язку становить N = m −(n −1) , де m – кількість віток, n – кількість вузлів графа. На

рис.2.46, б жирними лініями виділено одне з можливих дерев схеми рис.2.46, а, на якому 1, 3, 4 – вітки дерева.

Вітки 2, 5, 6, 7, 8 для даного дерева є вітками зв’язку.

Для не зв’язаних у топологічному сенсі графів схеми кількість зв’язків дорівнює N = m −(n −1) +Q −1 = m −n +Q , де Q – кількість не зв’язаних частин

графа.

Рисунок 2.47 – Графи: а – непланарний; б – направлений

Перехід до направленого графа дозволяє здійснити аналітичний запис структури графа, у вигляді таблиць-матриць, які називають топологічними матрицями. Аналітичне подання графа необхідне для формування і аналізу рівнянь складної схеми з допомогою ЕОМ.

2.10.2 Матриця з’єднань (вузлова)

Повне описання структури направленого графа дає n×m матриця з’єднань, n рядків якої є порядковими номерами вузлів, а m стовпців – номерами віток. Елементами aik цієї матриці є символи наявності чи відсутності вітки k, приєд-

наної до вузла i, які приймають значення +1 для вітки, яка виходить з вузла, значення –1 для вітки, яка входить у вузол і 0 – для вітки, не зв’язаної з вузлом. Щоб записати матрицю з’єднань, достатньо для кожної вітки визначити номери обох з’єднуваних нею вузлів i, j; заповнити клітинки на перетині рядків i, j та стовпця з номером вітки k значеннями +1, –1; в решті клітинок записати нулі.

Повна вузлова матриця визначає схему електричного кола.

Вона дозволяє подати геометричну структуру кола мовою алгебри, що має важливе практичне значення при аналізі електричних кіл.

З аналізу повної матриці з’єднань (A0 ) видно, що кожний її стовпець складається з двох ненульових елементів +1, −1. Ця властивість матриці (A0 ) ви-

пливає з того, що кожна вітка з’єднана з двома вузлами.

Сума чисел у довільному стовпці матриці дорівнює нулю. Це означає, що один з рядків матриці (A0 ) може бути одержаний лінійною комбінацією інших

рядків. Позбутися лінійної залежності рядків можна шляхом викреслювання довільного рядка в матриці (A0 ). В результаті викреслювання, наприклад, чет-

Матрицю (A) називають просто матрицею зв’язків, або вузловою матри-

цею. Вузол, відповідний якому рядок відкидається, називають базисним. Перестановка стовпців або рядків відповідає тільки зміні нумерації віток,

але не змінює схему кола.

Якщо елементи стовпців матриці (A) домножити на потенціали відповідних вузлів і підсумувати, то одержимо напруги відповідних віток, тобто

Слід зазначити, що вираз (2.68) та наступні формули, записані для кола постійного струму, можна використовувати також для кіл синусоїдного струму, застосувавши комплексне подання струмів, напруг, ЕРС, опорів, провідностей (див. підрозд. 3.10).

Систему рівнянь (2.68) можна записати в наступній матричній формі:

стовпці напруг віток та вузлових напруг; транспонована матриця (A).

Якщо елементи рядків матриці (A) домножити на струми відповідних віток, підсумувати і прирівняти до нуля, то одержимо рівняння, записані згідно з

2.10.3 Матриці параметрів елементів схеми

Складаючи матричні рівняння, що описують процеси в схемі, необхідно параметри віток – опори, провідності, ЕРС і струми джерел теж записувати в матричній формі.

Матриця опорів (провідностей). Матриця опорів (Rв) і матриця провідностей (Gв) є квадратними, їхній порядок дорівнює кількості віток. По діагоналі матриці записують власні опори (провідності) віток. Матриця провідностей є оберненою матриці опорів, тобто (Gв )=(Rв )−1 .

Якщо взаємних зв’язків між вітками немає, то матриці будуть діагональними. Якщо коло містить реактивні елементи L, C, та між вітками за рахунок спільного електромагнітного поля існують взаємні зв’язки, на перетині і-го рядка та j-го стовпця записують опори взаємного зв’язку між і-ю та j-ю вітками. Такий зв’язок виникає, наприклад, у колі синусоїдного струму. Тоді опори та провідності віток записують у комплексній формі (визначення комплексних опорів Z та провідностей Y елементів L, C, М розглянуто далі у розд.3.).

Наприклад, матриця опорів для кола, що містить чотири вітки із взаємно індуктивними зв’язками між всіма вітками, має наступний вигляд:

Якщо коло задовольняє умові взаємності, тобто Z ij = Z ji (Y ij =Y ji ), тоді матриця (Z в ) або (Y в) буде симетричною.

Приклад 2.12. Для схеми (рис.2.48,а) скласти матрицю опорів віток. Розв’язання. Матрицю опорів кола записують у такий спосіб. Номери рядків і

стовпців відповідають номерам віток. На головній діагоналі записують власні опори віток, а на перетині і-го рядка і j-го стовпця – опори взаємної індукції. При цьому опори взаємної індукції додатні, якщо в двох індуктивно зв’язаних котушках струми спрямовані однаково відносно однойменних затискачів (позначених у схемі зірочками). При різних напрямах струмів відносно однойменних затискачів опори взаємної індукції від’ємні.

Нумерувати вітки можна довільно, але з метою одержання матриці більш упорядкованого вигляду рекомендується спочатку нумерувати всі індуктивні елементи, потім резистивні і, насамкінець, ємнісні елементи (див. рис.2.48,а).

Матриця опорів для схеми (рис.2.48,а) має наступний вигляд:

Цю матрицю доцільно розглядати як складну і поділити на підматриці прямокутними контурами. Тоді матрицю (Z в) можна записати у вигляді:

контуру, утвореного джерелом і паралельною йому віткою в напрямі вітки, додатній напрям струму джерела збігається з напрямом обходу. Якщо струм джерела протилежний напряму обходу контуру, то перед відповідним струмом в матриці струмів джерел ставлять знак «мінус».

2.10.4 Закон Ома у матричній формі

Для довільної k-ї вітки схеми (рис.2.48,б) закон Ома можна записати у вигляді рівняння