
тюмгу / Тишин В.В. Дискретная математика в примерах
.pdfХлХ'
Имеем: у = q[ v x1 ■q'2 v x\ ■q2 .
Итак, ql = x \-x 2 - q \ , q2 = xl \/ x2 - q \, y = q[\'X l - q'2 v x\ ■q2 .
5. Строим схему из функциональных элементов типа конъюнкция, дизъюнкция, отрицание и элементов задержки.
Задание 6.3.2
1. Удалить из данной схемы задержки и написать формулы для функций
Ч1>Ч2>Чз>У-
2.Построить таблицы для функций, найденных в п. 1
3.Свести таблицы, найденные в п.2 в одну, провести кодировку.
4.Провести минимизацию автомата.

5.Для минимального автомата провести обратную кодировку, написать
“физическую “ таблицу переходов и выхода.
6.С помощью карт Карнау написать формулы функций перехода и вы хода.
7.Реализовать найденные функции схемами из функциональных эле ментов типа конъюнкция, дизъюнкция и отрицание .
8.Изобразить схему из функциональных элементов типа конъюнкция, дизъюнкция, отрицание и задержек, реализующую минимальный ко нечный автомат.
Таблица 6.3.2


10
11 |
12 |
Таблица 6.3.2(продолжение)

Таблица 6.3.2(продолжение)

Таблица 6.3.2(продолжение)
Таблица 6.3.2(окончание)
Пример решения задания 6.3.2
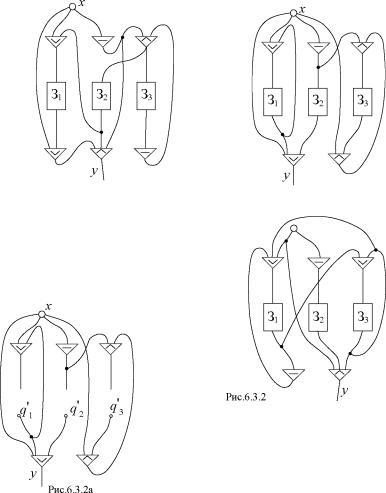
Решим задание 6.3.2 для данной схе мы (рис. 6.3.2):
1. Удалим задержки (рис.6.3.2а), введём три новых полюса cj\ ,q2 и с/3, соответствую
щих выходам задержек, а входам задержек будут соответствовать вершины , q2 и q2 .
Проведём анализ схемы, напишем формулы для функций q^,q2,q2 и V.
ql = x \/q l ', q2 - x \ = x /\q \ д х = 0; y = x \z q l v q 2.
2. Напишем таблицы найденных функций |
|
|
|
|
|||||
Таблица для |
ql =хv ql(табл. 6.3.2а): |
|
|
|
|
||||
|
|
|
|
|
|
|
|
Таблица б.3.2а |
|
\ад2<7з |
ООО |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
|
|
|
|
|
|
|
||
X |
\ |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Таблица для q2 - x |
(табл. 6.3.2Ь): |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Таблица б.3.2Ь |
|
\ а |
д 2<7з |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
|
|
|
|
|
|
||
х\
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Таблица для у = x v ql v q2 (табл. 6.3.2с):
|
|
|
|
|
|
|
Таблица 6.3.2с |
|
Х 'М г'й |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
|
|
|
|
|
|
|
х \ |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3. Сведём построенные таблицы в одну (табл. 6.3.2d): |
|
|
||||||
|
|
|
|
|
|
|
Таблица 6.3.2d |
|
\q tf2q2 |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
0 |
010,0 |
010,1 |
010,1 |
010,1 |
110,1 |
110,1 |
110,1 |
110,1 |
1 |
100,1 |
100,1 |
100,1 |
100,1 |
100,1 |
100,1 |
100,1 |
100,1 |
Закодируем наборы значений |
: |
0 0 0 - 1; 001 - 2; 010 - 3; 011 - 4; 100-5; 101-6; 110-7; 111-8.
Перепишем сводную таблицу, заменяя трёхразрядные двоичные наборы их кодами (табл.6.3.2е):
Таблица б.3.2е
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
X |
|
|
|
|
|
|
|
|
0 |
2 , 0 |
2 , 1 |
2 , 1 |
2 , 1 |
7 ,1 |
7 , 1 |
7 , 1 |
7, 1 |
1 |
5 Д |
5 Д |
5 Д |
5 Д |
5 Д |
5 Д |
5 Д |
5 Д |
4. Минимизируем полученный автомат по числу внутренних состояний. Строим треугольную таблицу (табл. 6.3.2f):
Таблица 6.3.2f
2
3
4
5
6
7
8
1 |
2 |
3 |
4 |
5 |
6 |
7 |
