Методы одномерной оптимизации

Метод сканирования основан на табулировании функции в некотором интервале [a,b] значений функции с шагом h:

h = (b-a)/n (28)

где n – количество интервалов разбиения. Последовательно определяются значений функции f(x) во всех точках разбиения аргумента и запоминается наименьшее значение функции R_м и положение минимума (х_м) (см. рис. 2).

а

b

h

x_м

R_м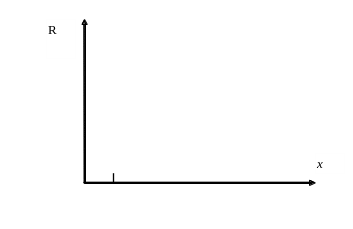

Рис. 2. Метод сканирования

Если в качестве шага сканирования выбрать заданную точность определения положения минимума , как это сделано в программе 12, то с этой точностью и получим искомое решение.

В программе 12 реализован метод сканирования одномерной функции R=f(x). Построением графика функции f(x) решается задача отделения одного экстремума. При желании, сканирование можно повторить с новым диапазоном поиска минимума. Эту же программу можно использовать для нахождения максимумов, если в программе сканирования в операторе while x  b знак  заменить на . В общем же случае любую программу находящую минимум функции можно превратить в программу поиска максимума, если выражение для функции заключить в скобки и поставить перед ними знак минус.

Программа 12

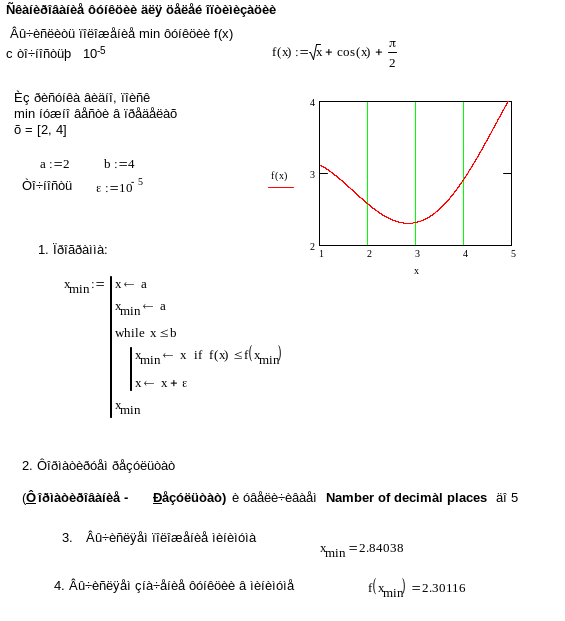
Метод требует длительных и объемных вычислений для получения минимума с высокой точностью. К достоинствам метода можно отнести тот факт, что алгоритм вычислений очень прост и кроме вычислений функции, практически никаких дополнительных вычислений не требуется. Рекомендуется использовать этот метод для функций, не требующих длительного времени их вычисления. Можно значительно сократить количество обращений к вычислению функции, если использовать методы, описанные ниже. Все они используют итерационные процедуры. На каждом шаге происходит уменьшение первоначального интервала [a,b] поиска.

Эффективность этих методов разная. Коэффициент K эффективности алгоритма тем больше, чем больше степень сжатия интервала поиска на каждом шаге оптимизации и тем меньше количество вычислений функции. Для метода сканирования можно рассчитать:

(29)

где S – количество вычислений функции, за которое начальная длина L диапазона, в котором находится минимум целевой функции, уменьшается до l.

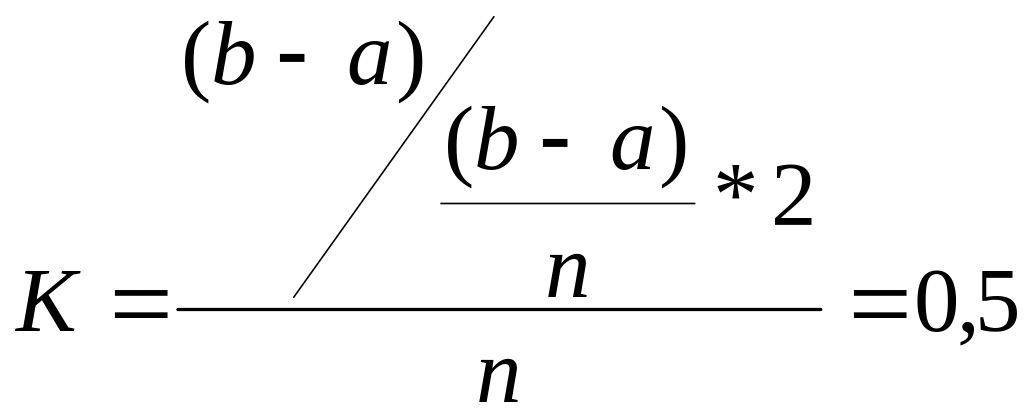(30)

Очевидно, что для увеличения коэффициента эффективности алгоритма надо увеличить степень сжатия диапазона поиска и уменьшить количество вычислений функции. Рассмотрим для этого алгоритм метода дихотомии, описанный в [10].

Метод дихотомии заключается в следующем. Начальный диапазон поиска делится пополам: х = (a + b)/2 . Затем определяют с какой стороны от х находится минимум. Сравнивают значения функции R(x+) и R(x-), где  – некоторая малая величина, выбираемая в начале программы, которая в конце процедуры окажется погрешностью определения минимума. На рис. 3 минимум оказался слева, далее поиск продолжают в диапазоне новых значений a,b, причем b=x, а величина a остается прежней.

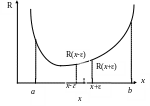
Рис. 3. Метод

дихотомии

Таким образом степень сжатия на каждом шаге оптимизации равна 2, при этом число вычислений функции равно 2, следовательно К=1. То есть эффективность метода дихотомии в 2 раза выше, чем сканирования.

Программа 13

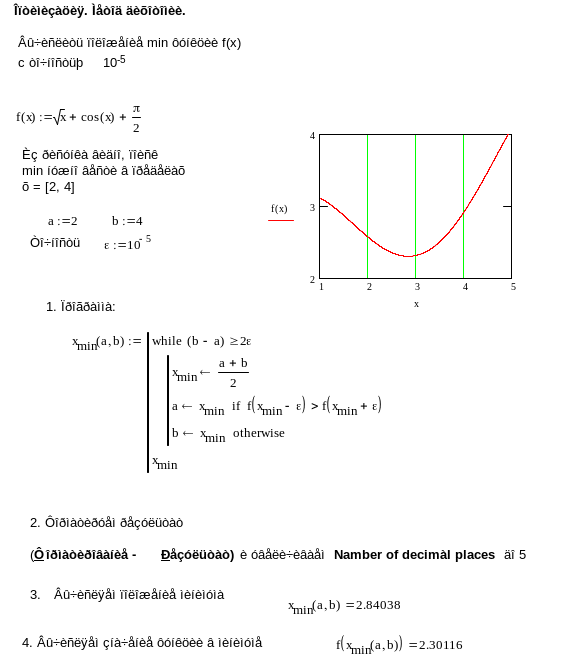
Метод золотого сечения. Одним из наиболее эффективных методов по критерию К является метод золотого сечения. “Золотым сечением” или “золотым отношением” называют такое деление отрезка на две части, что “целое к большему относится также, как большее к меньшему”.

Можно показать, что отношение малой части отрезка к целому равно

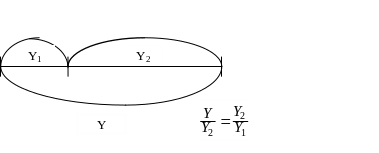
В методе золотого сечения первоначальный отрезок (a, b) делится на части точками х₁ и х₂, причем обе точки делят отрезок в золотом соотношении с разных сторон:

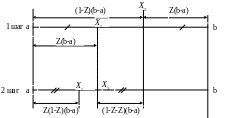
Затем сравнивают значения целевой функции R(X₁) и R(x₂). Если R(X₁) > R(x₂), то минимум функции, очевидно, находится в интервале (X₁, b). Если наоборот, R(X₂) > R(x₁), то минимум надо искать в диапазоне (a, X₂), как это показано на рисунке. На втором шаге новый диапазон поиска также делится в золотом соотношении с двух сторон. И здесь оказывается, что вычислять значение функции R(x₂) на втором шаге не надо – оно уже было вычислено как R(X₁) на первом шаге. Можно показать, что Z(1-Z)(b-a)=(1-Z-Z)(b-a), если Z – “золотое отношение”.

Степень сжатия интервала поиска в этом методе составляет

Это меньше, чем в методе дихотомии, однако за счет того, что эта степень сжатия достигается не за два, а за одно вычисление функции, коэффициент эффективности в методе золотого сечения больше, чем в полтора раза выше по сравнению с методом дихотомии.

Программа 14

Существует метод одномерной оптимизации, использующий числа Фибоначчи. Этот метод также требует одного вычисления функции на шаге и имеет немного больший коэффициент сжатия, чем в методе золотого сечения. Однако, этот коэффициент не постоянный и при большом числе шагов стремится к 1.618, т. е. эффективность этих методов примерно одинакова.

Для целей отделения экстремумов и нахождения экстремумов очень можно использовать встроенные функции MathCad. После построения графика одномерной функции и отделения экстремумов можно вычислять минимумы и максимумы функции по-отдельности, как это показано в программе 15.

Программа 15

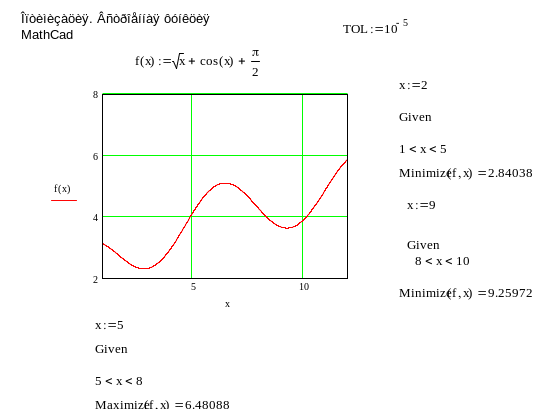
Из листинга программ 12–15 видно, что в пределах заданной точности все методы дают одинаковые результаты.