Варианты творческих заданий
1. Проведите аппроксимацию табличных данных Y=f(X) полиномом, причем выбор оптимальной степени полинома проведите одним из методов, описанных в этой главе.
2. Проведите аппроксимацию табличных данных Y=f(X) нелинейной функцией, минимизируя сумму квадратов отклонений (нелинейный МНК) одним из методов, описанных в этой главе. Функцию и табличные данные можно взять у преподавателя.
Глава 5. Интегрирование
При изучении химии, в частности физической химии, очень часто встречаются закономерности, которые описываются дифференциальными уравнениями. Примером может служить раздел физической химии, посвященный термодинамике химических процессов. Температурные зависимости термодинамических функций (энтальпии, энтропии, энергии Гиббса) и константы равновесия реакции описываются соответствующими дифференциальными уравнениями, которые в общем виде могут быть записаны как
dy/dx = f(x) (31)
Решить уравнение (31) относительно y можно тремя различными путями.
1. Разделить переменные, проинтегрировать полученное выражение и получить аналитическое выражение для y:
y = yo + F(x) (33)
где F(x) – первообразная функции f(x); y0 – постоянная интегрирования.
2. Уравнение (31) записать в интегральной форме:
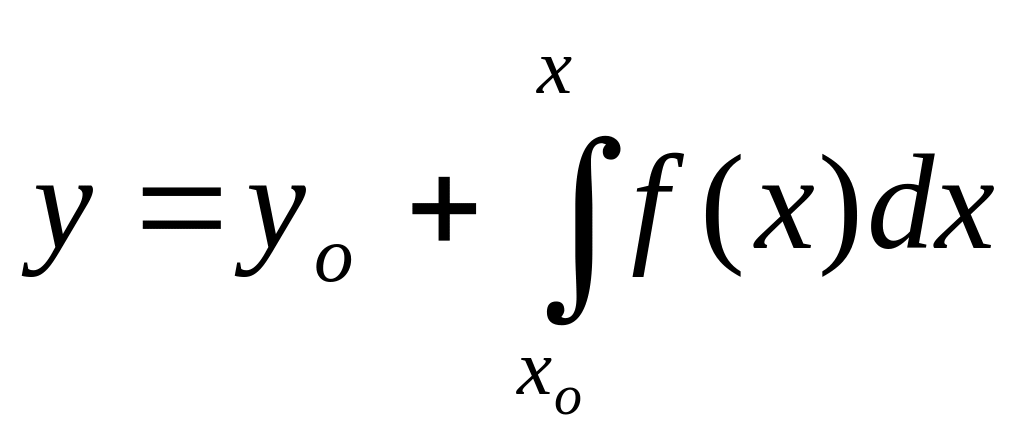(34)
и вычислить интеграл одним из численных методов интегрирования.
3. Можно решить непосредственно дифференциальное уравнение (31) численным методом.
В отличие от приближенных методов расчета по уравнениям (31) и (34), решение с помощью уравнения (33) называют «точным». Методы получения аналитического решения дифференциальных уравнений студенты изучают в дисциплине «Высшая математика», некоторые практические приложения такого решения можно найти в дисциплине «Физическая химия», например, в разделе «Термодинамика химических реакций». Двум другим способам решения дифференциальных уравнений посвящены настоящая и последующая глава. Как мы увидим далее в реальных вычислениях, точность приближенных методов не уступает «точным».
Вычисление определенных интегралов
Вычисление определенного интеграла численными методами основано на трех основных положениях:
интеграл
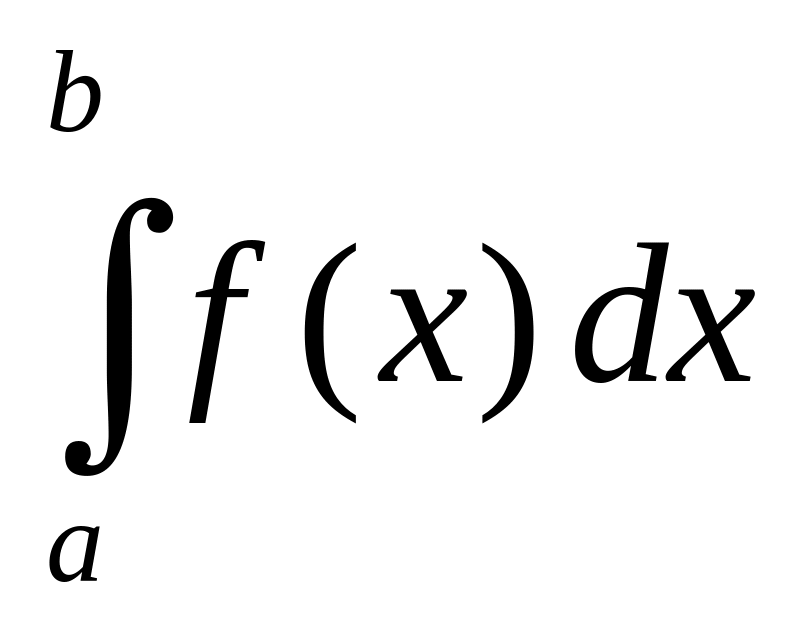численно равен площади под кривой
f(x),
ограниченной абсциссами a,
b и осью х;
истинная кривая f(x) аппроксимируется какой-либо простой функцией, интегрирование которой не представляет труда;
для уменьшения ошибки усечения общую площадь под кривой делят на N частей вертикальными линиями, чаще всего с постоянным шагом h=(b-a)/N и на каждом малом интервале применяют одну и ту же аппроксимирующую функцию. Затем значения отдельных интегралов суммируются.
Рассмотрим подробно схему получения расчетной формулы для вычисления интеграла согласно этим положениям.
Метод прямоугольников
1. Выбор аппроксимирующей функции. Самым простым и надежным способом является представление аппроксимирующей функции в виде полиномов различной степени. Пусть степень полинома равна нулю. Тогда аппроксимирующая функция имеет вид:
Y(x) = f(a) (35)
Тогда приближенное значение интеграла равно заштрихованной области на рис. 4, а, т. е. площади прямоугольника (поэтому и метод называется методом прямоугольников):
(36)
Тот же результат мы получим, если аппроксимирующую функцию мы подставим вместо истинной функции и возьмем табличный интеграл:
(37)
2. Теперь разделим интервал на N частей с постоянным шагом h (рис. 4, б) и на каждом малом интервале проведем аппроксимирующую функцию. Таким образом, площадь под кривой f(x) в этом случае равна сумме площадей прямоугольников y0, y1, y2 … yn-1. Площадь отдельного прямоугольника можно вычислить как произведение шага на значение функции. Таким образом, получаем расчетную формулу прямоугольников:
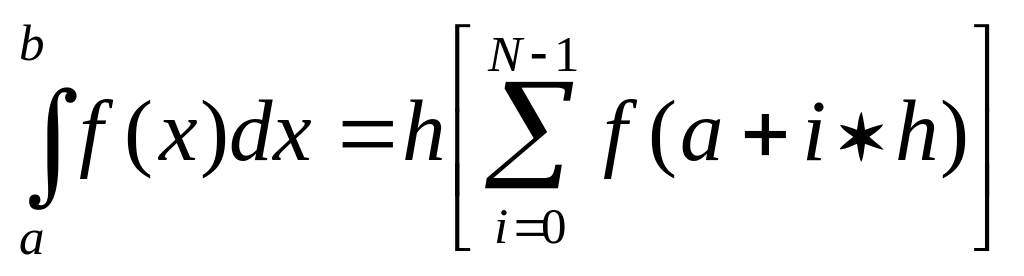(38)
f(x)
Ошибка усечения
f(a)
x a
b
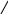
а) аппроксимирующая функция на всем интервале интегрирования
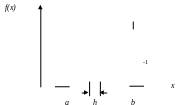
б) аппроксимирующая функция на каждом малом интервале
Рис. 4. Метод прямоугольников
Та часть общей площади под кривой f(x), которая не вошла в заштрихованную область, очевидно, есть погрешность вычисления интеграла, ее называют «ошибкой усечения». Чем меньше шаг, тем меньше ошибка усечения. Однако слишком сильно уменьшать шаг интегрирования нельзя. С уменьшением шага интегрирования резко возрастает объем вычислений, особенно если сама подынтегральная функция требует больших вычислений. При этом растет и так называемая «ошибка округления». Для современных многоразрядных и быстродействующих машин это может показаться неактуальным, но учитывать такую возможность надо. Ошибку усечения можно уменьшить и другим способом, применив в качестве аппроксимирующей функции полином более высокой степени. Например, можно взять полином первой степени (метод трапеций), вместо нулевого (метод прямоугольников).