
- •Математический анализ
- •1.Пределы
- •2.Элементы дифференциального исчисления
- •1. Производная
- •2. Дифференциал
- •3. Производные высших порядков
- •4. Исследование функций
- •3.Элементы интегрального исчисления
- •1. Неопределенный интеграл
- •2. Определенный интеграл
- •4.Функции нескольких переменных
- •1. Частные производные
- •2. Кратные интегралы
- •6.Дифференциальные уравнения
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения
2. Определенный интеграл
Пусть требуется найти площадь плоской фигуры, ограниченной графиком непрерывной функции y = f(x), осью абсцисс и прямыми x= a, x = b при условии, что f(x) неотрицательна на отрезке [a, b]. Такая фигура называется криволинейной трапецией, отрезок [a, b] является ее высотой и боковой стороной, то есть трапеция «лежит на боку». Другая боковая сторона криволинейна, она образована графиком функции y = f(x). Основания трапеции лежат на прямых x= a и x = b; возможно, одна из них или обе вырождаются в точки.
Разобьем отрезок [a,
b] на n
равных частей длиной ∆x
=
![]() .
Точки деления обозначим x0
= a, x1,
x2, … , xn
= b. Через каждую из
этих точек проведем вертикальную
прямую. В результате криволинейная
трапеция разобьется на п криволинейных
трапеций высотой ∆x.
Для приближенного вычисления площади
заменим каждую из них на прямоугольник
с основанием ∆x, а
высоты этих прямоугольников возьмем
равными f(x0),
f(x1),
… , f(xn–1)
соответственно. Эти в
.
Точки деления обозначим x0
= a, x1,
x2, … , xn
= b. Через каждую из
этих точек проведем вертикальную
прямую. В результате криволинейная
трапеция разобьется на п криволинейных
трапеций высотой ∆x.
Для приближенного вычисления площади
заменим каждую из них на прямоугольник
с основанием ∆x, а
высоты этих прямоугольников возьмем
равными f(x0),
f(x1),
… , f(xn–1)
соответственно. Эти в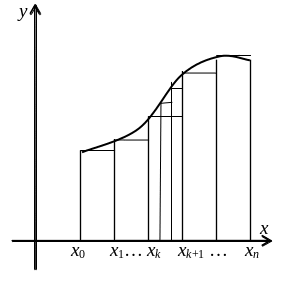 ысоты
являются левыми основаниями соответствующих
криволинейных трапеций.
ысоты
являются левыми основаниями соответствующих
криволинейных трапеций.
Сумма площадей прямоугольников равна (f(x0) + f(x1) + … + f(xn–1))∆x. Она отличается от площади криволинейной трапеции на небольшую величину: на рисунке верхняя граница криволинейной трапеции гладкая, а у объединения треугольников – ступенчатая. Разница между площадями образована небольшими заштрихованными кусочками, сглаживающими ступеньки. Эту разницу можно уменьшить, если уменьшить основания треугольников ∆x, то есть увеличить n. На рисунке отрезок [xk, xk+1] разбит еще на три части, и наглядно видно, как уменьшилась разница площадей.
В пределе при n → получим точное значение площади, то есть
![]() .
.
Эта формула подводит к определению определенного интеграла:
![]() .
.
Границы а и b называются пределами интегрирования. Сумма, стоящая под знаком предела, называется интегральной суммой. При этом не требуется, чтобы функция f(x) была неотрицательной, она может быть даже разрывной. Необходимо лишь, чтобы предел в правой части равенства существовал.
Определенный интеграл вычисляется с помощью формулы Ньютона – Лейбница, связывающей определенный и неопределенный интеграл:
![]() ,
,
где F(x)
– любая первообразная функции f(x).
При этом для краткости эту формулу
записывают в виде
![]() .
.
Пример 1.3.7.
![]() =
=![]() =
=![]() =
22.
=
22.
При вычислении определенных интегралов используют те же приемы, что при вычислении неопределенных интегралов. Но в их применении есть свои особенности. Если применяется замена переменной, то нет необходимости возвращаться к старой переменной. Вместо этого пересчитывают пределы интегрирования для новой переменной.
Пример 1.3.8.
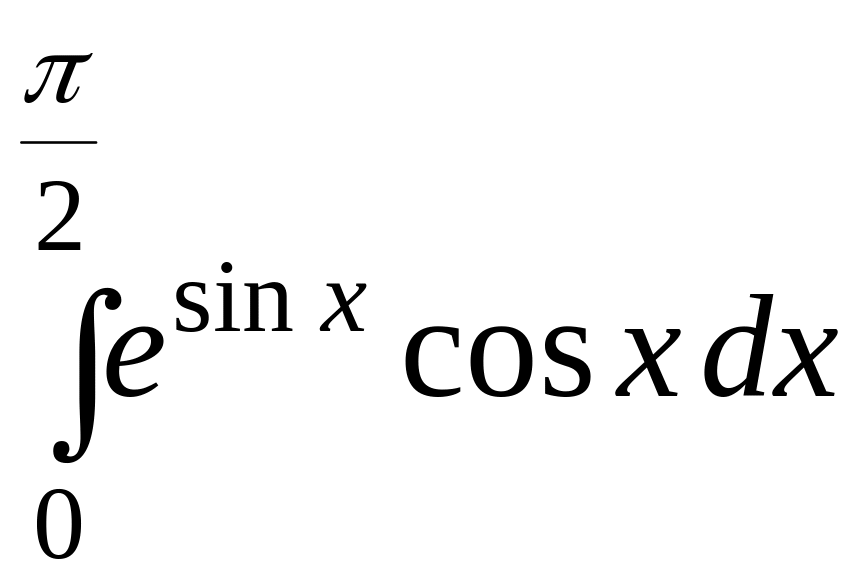 =/
=/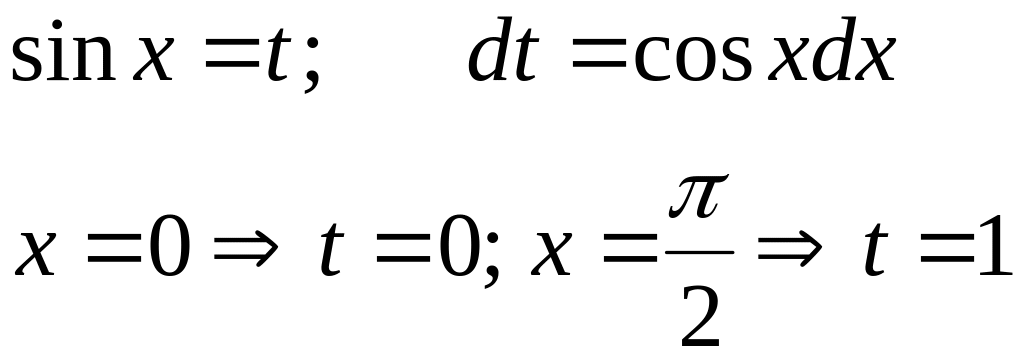 /=
/=![]() =
=
=![]() =
е – 1.
=
е – 1.
Пример 1.3.9.
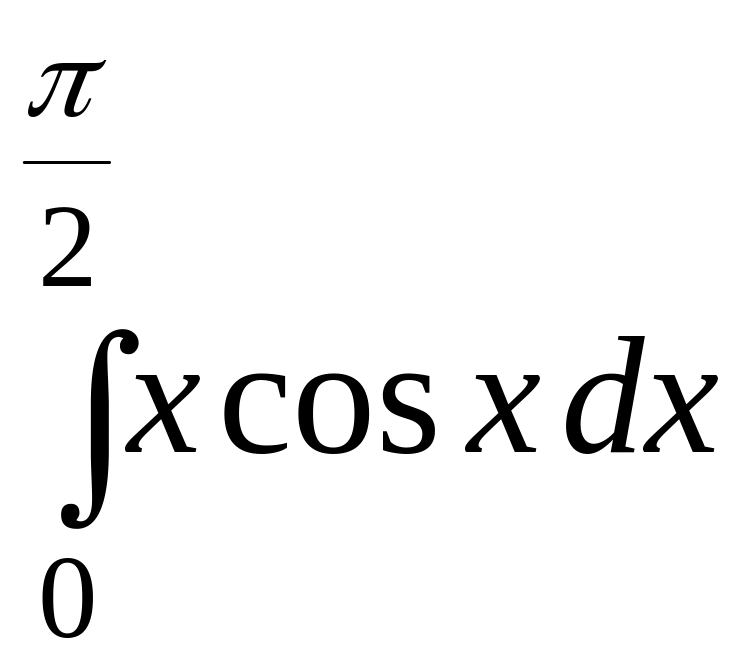 =
=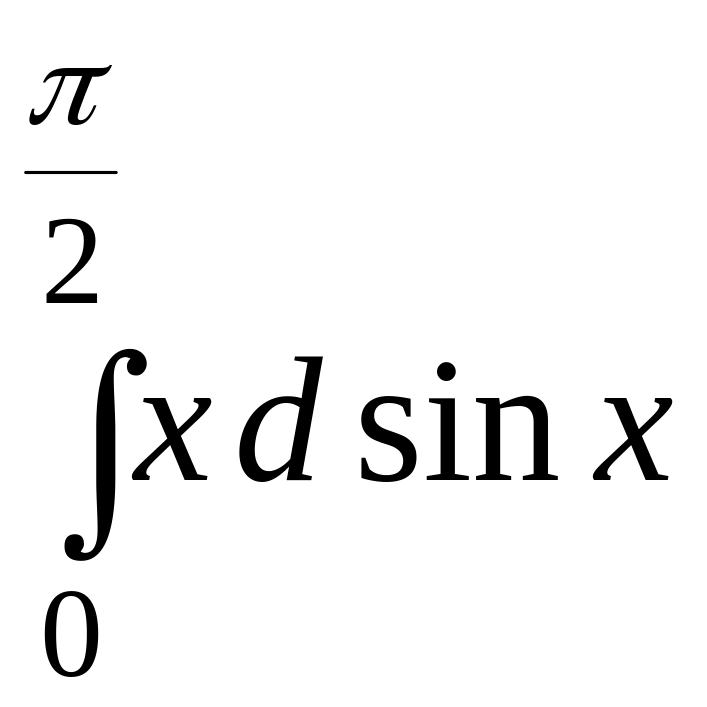 =
=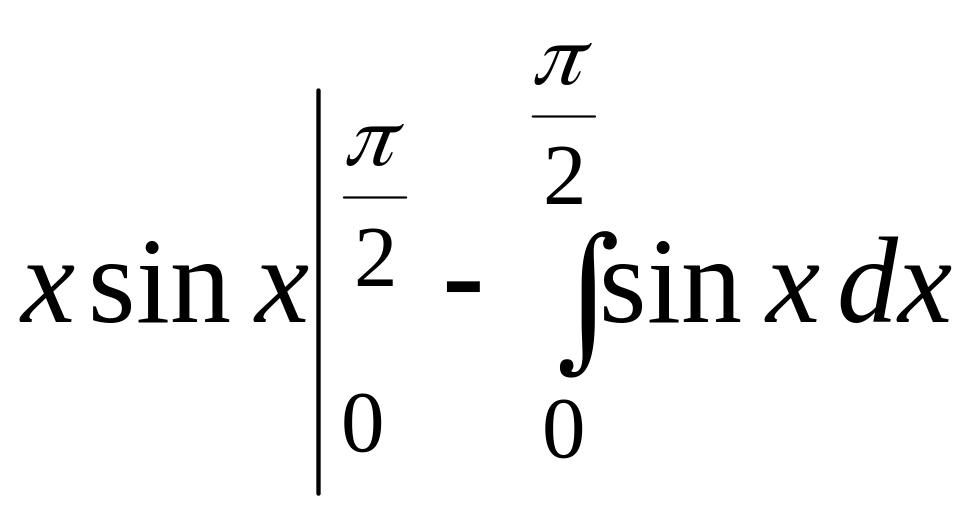 =
=![]() =
=![]() .
.
Свойства I – III неопределенного интеграла выполняются и для определенного интеграла. Имеют место и дополнительные свойства:
IV.![]() ;
;
V.
![]() .
.
Из построения определенного интеграла, описанного в начале пункта, ясен его геометрический смысл: это площадь криволинейной трапеции, ограниченной графиком функции f(x). Но это действительно так, только если функция неотрицательна на промежутке интегрирования. В общем случае это ориентированная площадь: если функция отрицательна на промежутке интегрирования, то получим площадь со знаком «минус». Если же функция меняет знак на промежутке интегрирования, то чтобы свести интеграл к площади, надо отдельно считать интеграл на промежутках, где функция неотрицательна, и на промежутках, где функция неположительна.
С помощью определенного интеграла можно считать площади плоских фигур. Если фигура ограничена справа и слева прямыми x = a, x = b, а сверху и снизу графиками y = f(x) и y = g(x) соответственно, то ее площадь вычисляется по формуле
![]() .
.
Пример 1.3.10. Найти площадь фигуры, ограниченной графиками функций y = x2 и y = x + 2.
Р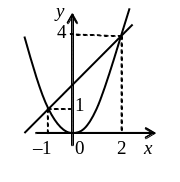 ешение.
Найдем сначала точки пересечения
графиков, решив уравнение x2
= x + 2. Его корни
–1 и 2, они являются пределами
интегрирования. Изобразим графики
функций, чтобы выяснить, какой из них
образует верхнюю границу фигуры и какой
нижнюю. Вычисляем искомую площадь:
ешение.
Найдем сначала точки пересечения
графиков, решив уравнение x2
= x + 2. Его корни
–1 и 2, они являются пределами
интегрирования. Изобразим графики
функций, чтобы выяснить, какой из них
образует верхнюю границу фигуры и какой
нижнюю. Вычисляем искомую площадь:
![]() =
=
![]() =
=
= 2 + 4 –
![]() –
+
2 +
=
–
+
2 +
=
![]() .
.
У п р а ж н е н и я
1.3.1. Найдите неопределенные интегралы:
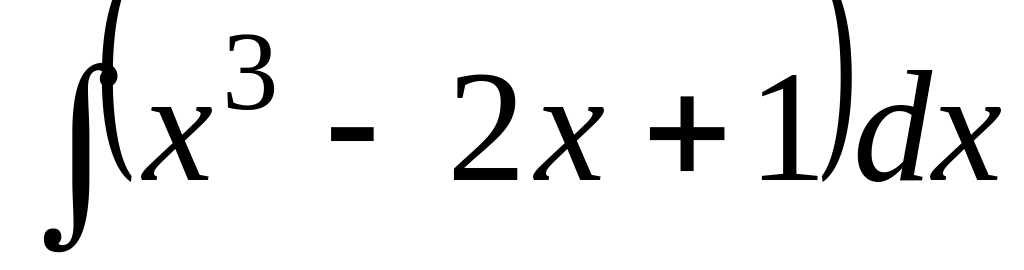 ;
;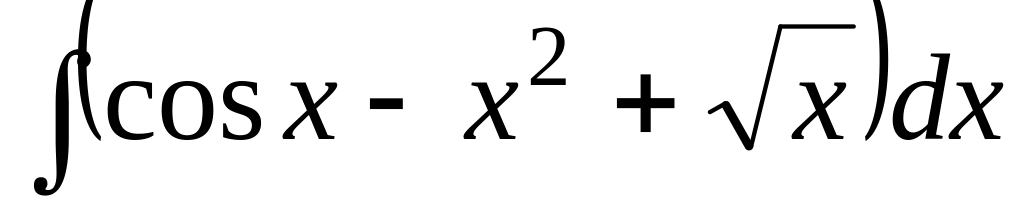 ;
;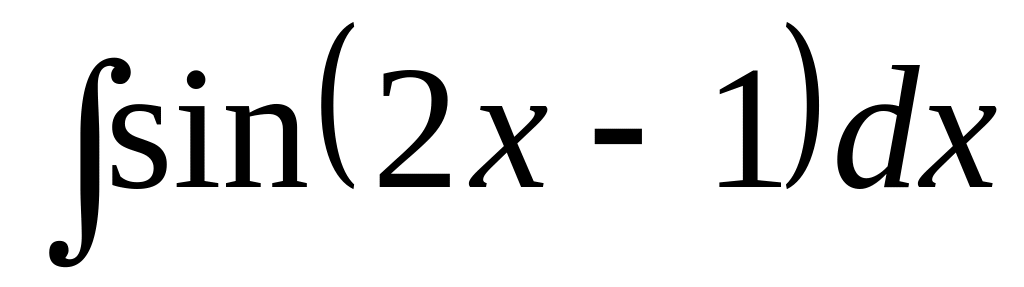 ;
;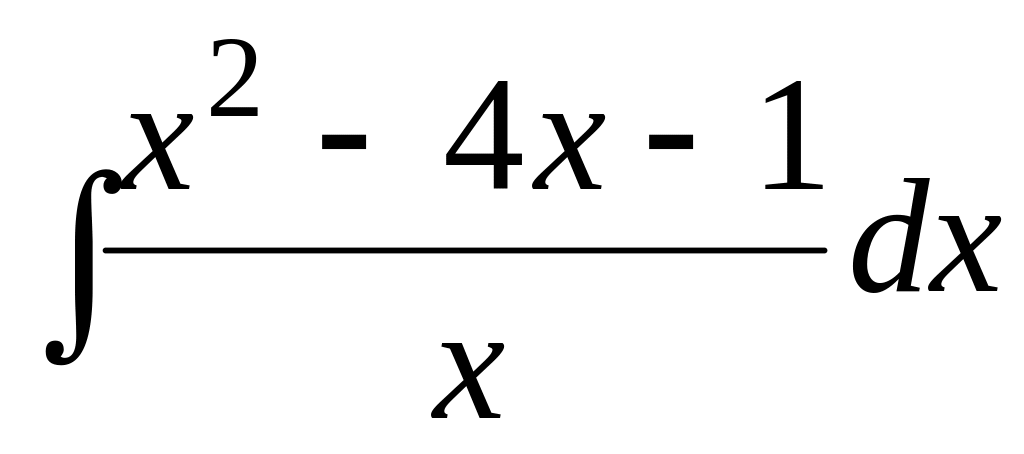 ;
;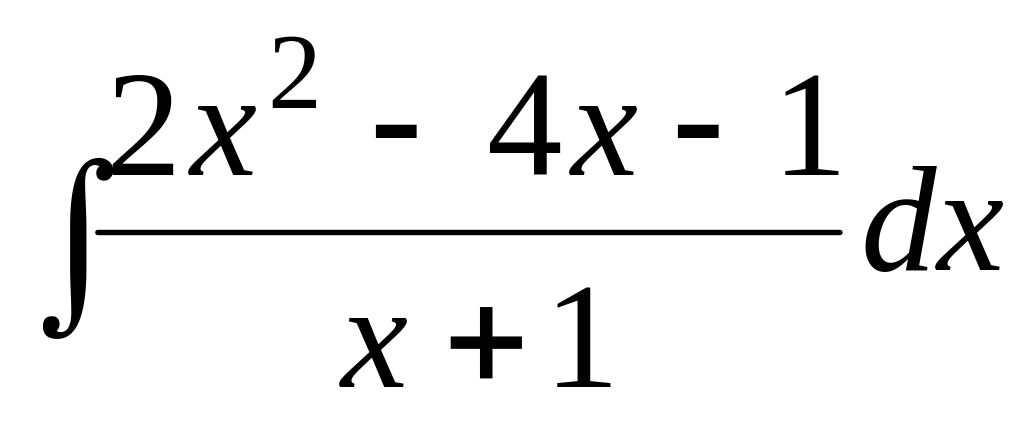 ;
;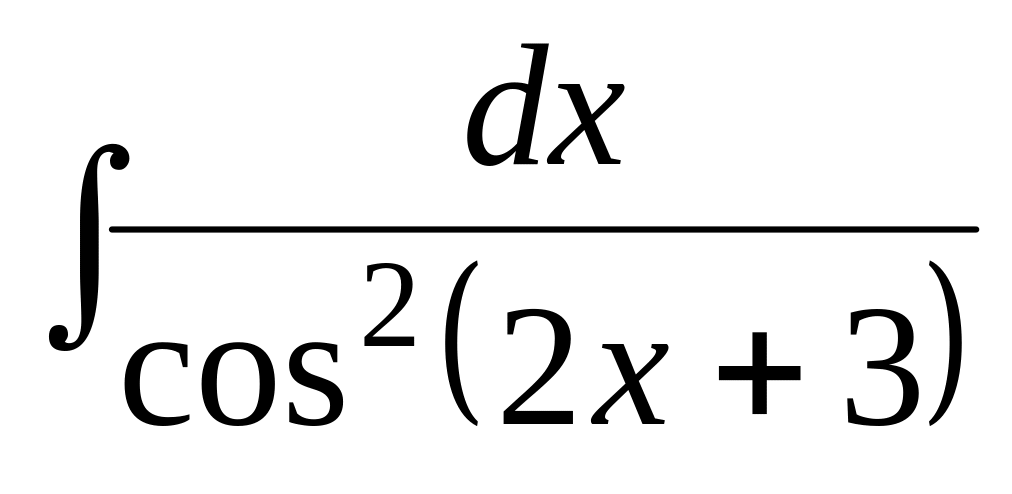 ;
;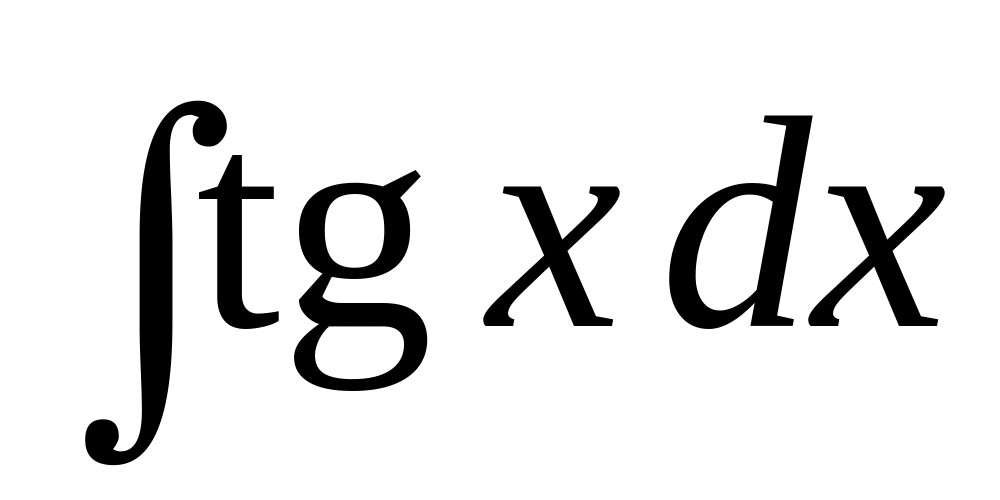
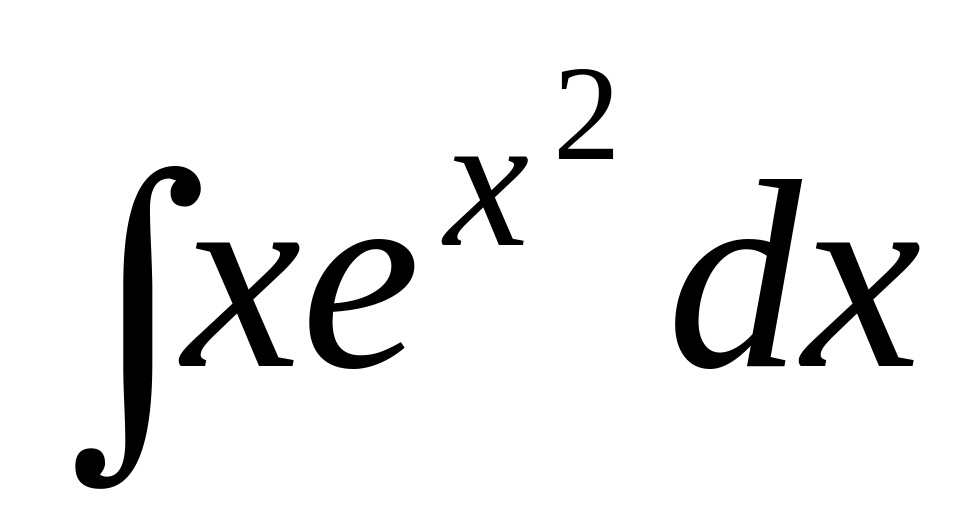 ;
;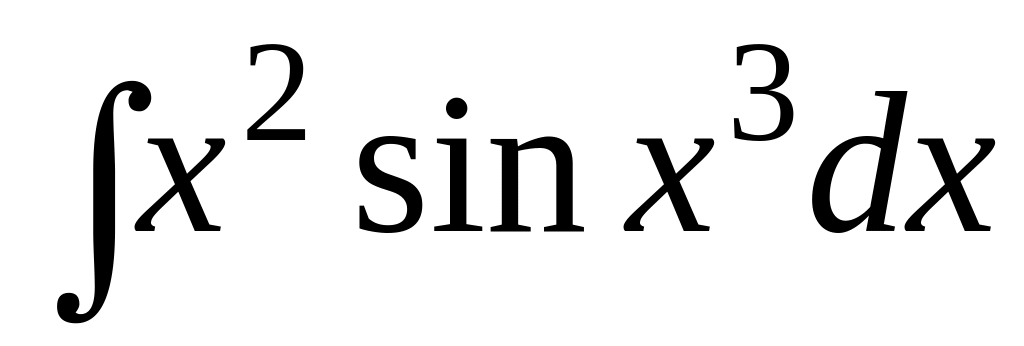 ;
;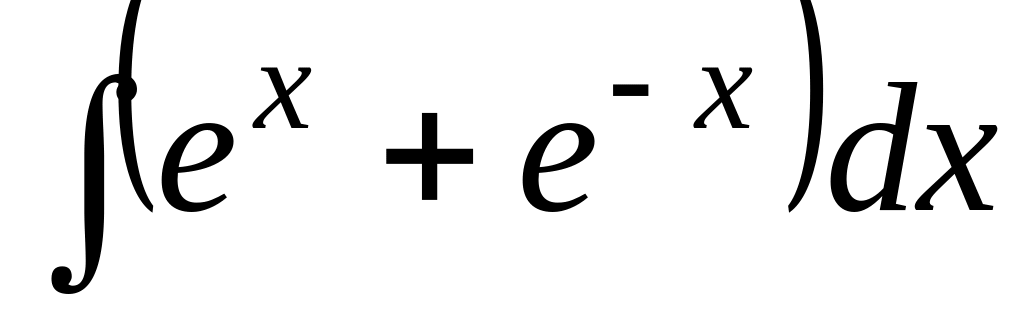 ;
;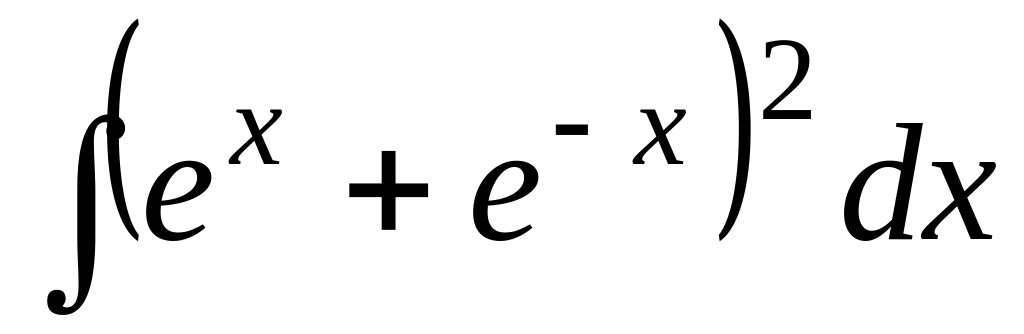 ;
;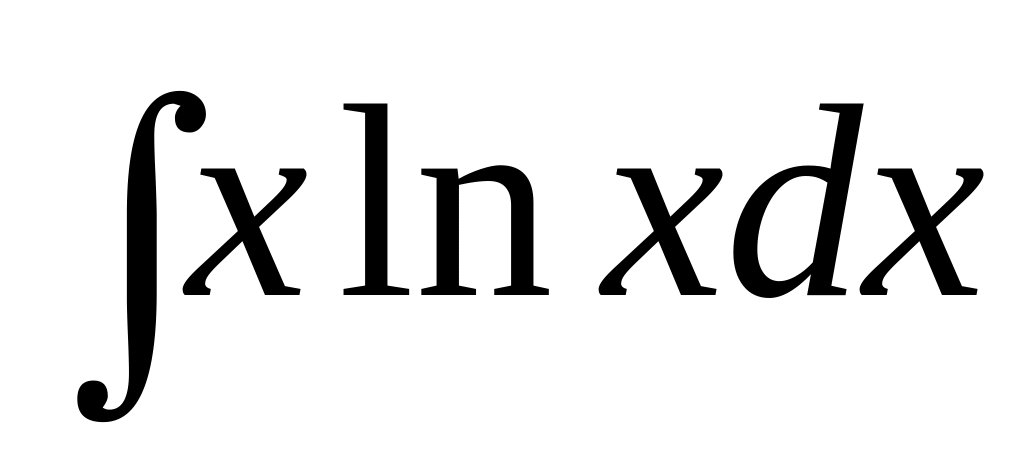 ;
;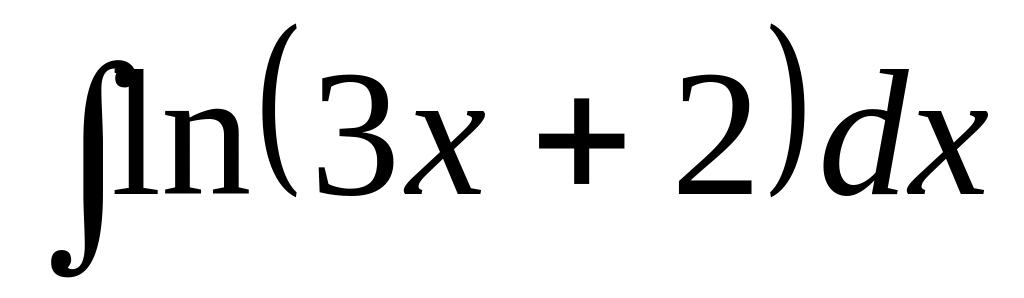 ;
;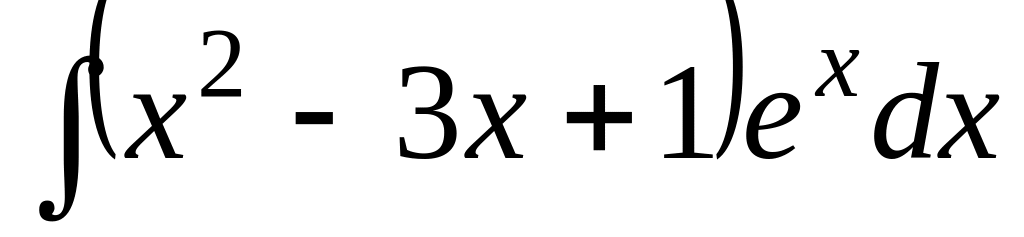 ;
;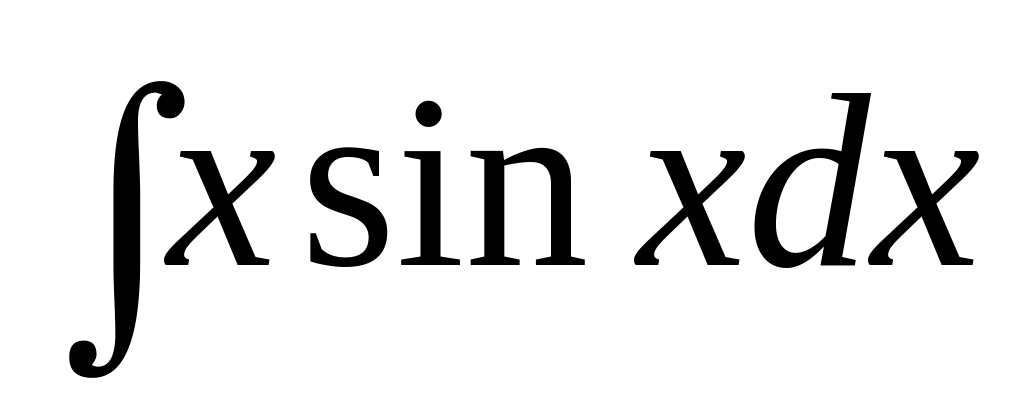 ;
;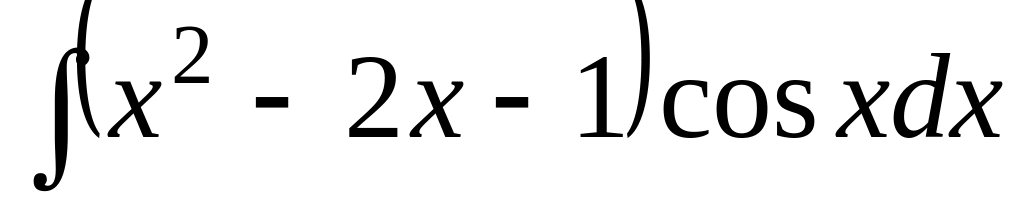 .
.
1.2.2. Вычислите определенные интегралы:
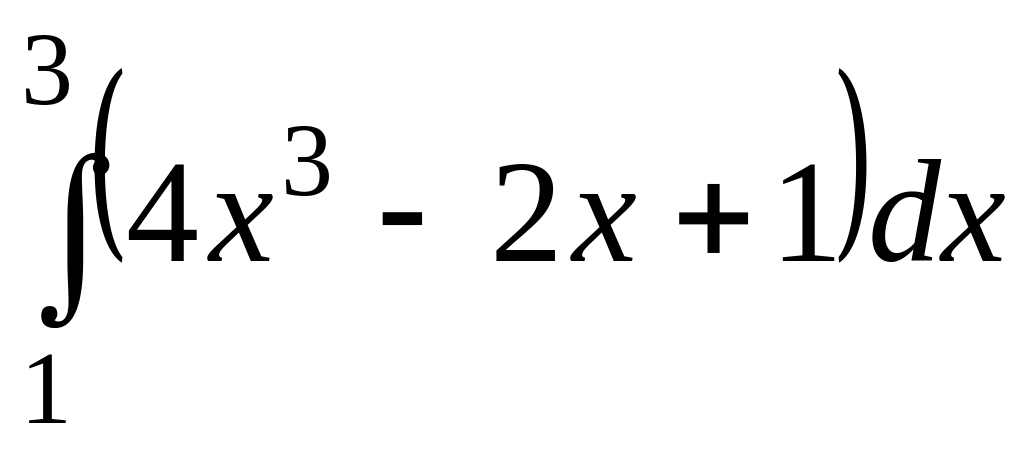 ;
;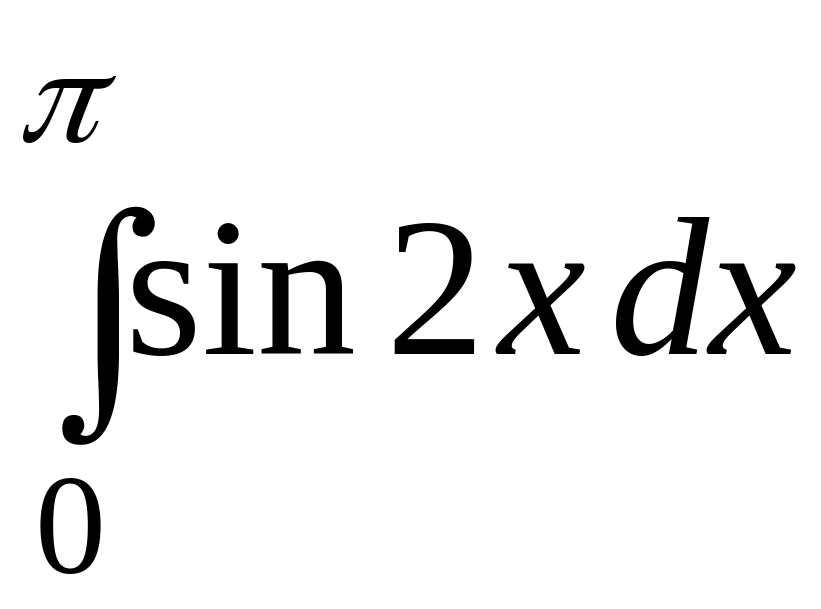 ;
;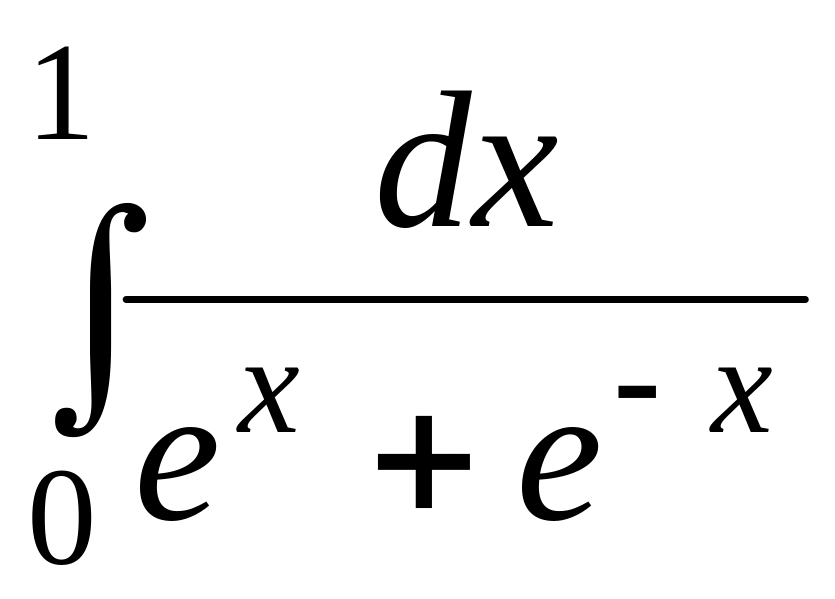 ;
;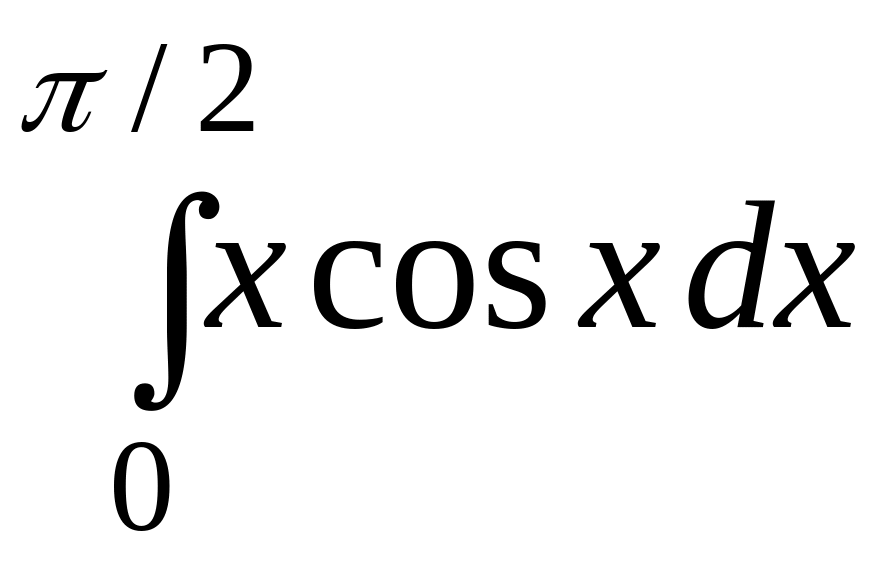 ;
;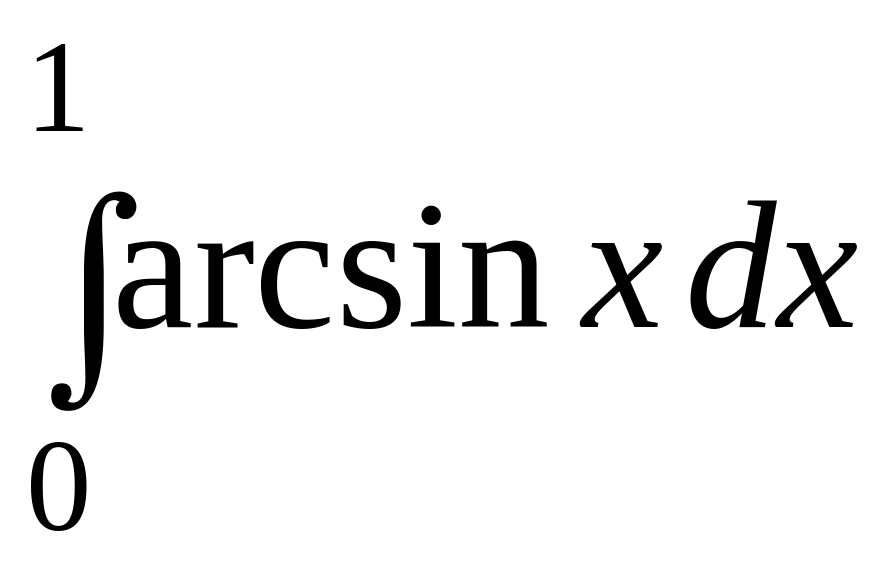 ;
;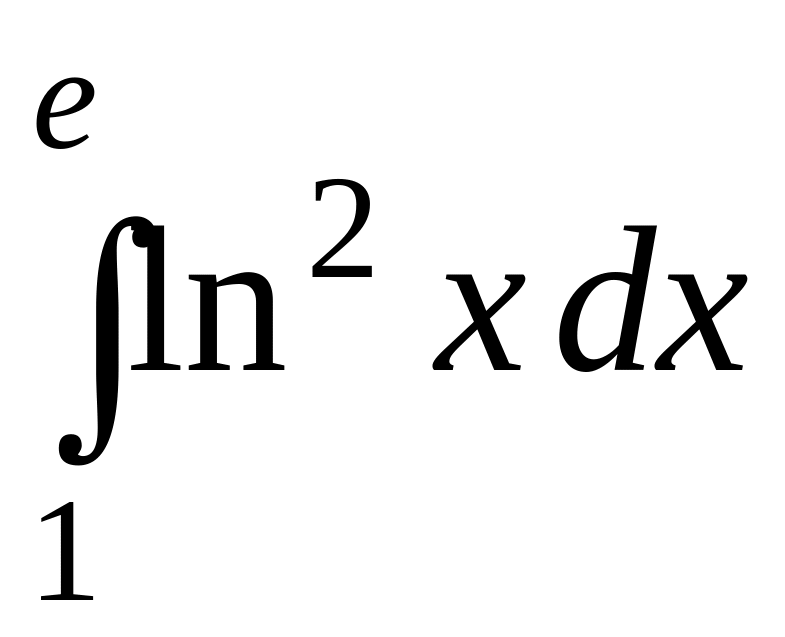 .
.
1.2.3. Найдите площадь фигуры, ограниченной линиями:
y = x2 – 1, y = 1 – x;
y = x2 – 3x + 2, y = –x2 + 5x – 2;
y = sin x, y = x – , x = 0;
y = 2x, y = x + 1.
