
- •Математический анализ
- •1.Пределы
- •2.Элементы дифференциального исчисления
- •1. Производная
- •2. Дифференциал
- •3. Производные высших порядков
- •4. Исследование функций
- •3.Элементы интегрального исчисления
- •1. Неопределенный интеграл
- •2. Определенный интеграл
- •4.Функции нескольких переменных
- •1. Частные производные
- •2. Кратные интегралы
- •6.Дифференциальные уравнения
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения
2.Элементы дифференциального исчисления
1. Производная
Пусть по городу движется машина
со скоростью 60 км/ч. Эта скорость показана
на спидометре. Но что означает это
показание? Как известно, скорость равна
отношению пройденного расстояния к
затраченному времени,
![]() .
Но это не значит, что за 1 час машина
действительно проедет 60 км. Возможно,
через 10 минут машина приедет в нужное
место и остановится. Можно сказать, что
60 км/ч = 1 км/мин, но даже за 1 минуту машина
не проедет 1 км, так как впереди горит
светофор красным светом, и через
полминуты машина остановится. В таком
случае можно сказать, что 1 км/мин =
.
Но это не значит, что за 1 час машина
действительно проедет 60 км. Возможно,
через 10 минут машина приедет в нужное
место и остановится. Можно сказать, что
60 км/ч = 1 км/мин, но даже за 1 минуту машина
не проедет 1 км, так как впереди горит
светофор красным светом, и через
полминуты машина остановится. В таком
случае можно сказать, что 1 км/мин =
![]() м/с, и это достаточно хорошо отражает
смысл показания спидометра. Но это
верно только в том случае, если машина
движется равномерно. Если же машина
начала торможение и в какой-то момент
на спидометре появилось показание 30
км/ч, то это не значит, что машина за
секунду проедет
м/с, и это достаточно хорошо отражает
смысл показания спидометра. Но это
верно только в том случае, если машина
движется равномерно. Если же машина
начала торможение и в какой-то момент
на спидометре появилось показание 30
км/ч, то это не значит, что машина за
секунду проедет
![]() м: в конце этой секунды скорость будет
меньше, и пройденное расстояние окажется
меньше. В этом случае можно рассматривать
промежуток времени в 0,1 с. Значение
скорости для этого промежутка также
окажется искаженным, но менее значительно.
Чем меньше мы возьмем длину временного
промежутка ∆t, тем
меньше будет искажение. Взять самый
маленький промежуток, чтобы получить
точное значение скорости, мы не можем:
такого просто не существует, его можно
уменьшать неограниченно. Но существует
математический аппарат, позволяющий
получить точное значение скорости, это
теория пределов. Пусть пройденное
расстояние s есть
функция от времени t,
то есть s = s(t).
Тогда расстояние, пройденное за
промежуток времени ∆t
начиная с момента t0,
равно s(t0+∆t)
– s(t0).
Мы имеем формулу
м: в конце этой секунды скорость будет
меньше, и пройденное расстояние окажется
меньше. В этом случае можно рассматривать
промежуток времени в 0,1 с. Значение
скорости для этого промежутка также
окажется искаженным, но менее значительно.
Чем меньше мы возьмем длину временного
промежутка ∆t, тем
меньше будет искажение. Взять самый
маленький промежуток, чтобы получить
точное значение скорости, мы не можем:
такого просто не существует, его можно
уменьшать неограниченно. Но существует
математический аппарат, позволяющий
получить точное значение скорости, это
теория пределов. Пусть пройденное
расстояние s есть
функция от времени t,
то есть s = s(t).
Тогда расстояние, пройденное за
промежуток времени ∆t
начиная с момента t0,
равно s(t0+∆t)
– s(t0).
Мы имеем формулу
v
=
![]() . (1)
. (1)
Этой формуле соответствует показание скорости на спидометре машины в момент времени t0. Это так называемая мгновенная скорость. В отличие от нее формула показывает среднюю скорость на отрезке s или за промежуток времени t. В формуле (1) скорость вычисляется в момент времени t0. А так как этот момент можно выбрать произвольно, то вместо t0 можно взять просто t, и получим формулу для мгновенной скорости в произвольный момент t:
v
=
![]() . (2)
. (2)
Формула (2) подводит нас к определению производной для произвольной функции f(x):
![]() . (3)
. (3)
Р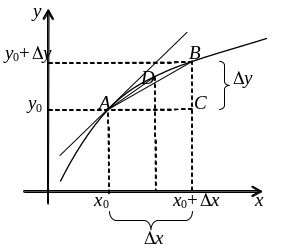 ассмотренный
выше пример раскрывает физический
смысл производной: если функция выражает
пройденное расстояние в зависимости
от времени, то ее производная – это
скорость. Поясним геометрический смысл
производной. На рисунке отмечены
значения аргумента x0
и x0+∆x
с заданным приращением аргумента ∆x.
Соответствующие значения функции y0
= f(x0)
и f(x0+∆x),
приращение функции ∆y
= f(x0+∆x)
– f(x0).
На графике функции соответствующие
точки обозначены А и В, приращение
аргумента ∆x равно
длине катета АС, а приращение функции
∆y – длине катета ВС
в прямоугольном треугольнике АВС.
Тогда отношение ∆x/∆y
равно тангенсу угла, образованного
секущей АВ с положительным
направлением оси абсцисс. Это отношение
стоит под знаком предела в формуле (3).
Если уменьшить значение ∆x,
на рисунке перейти от секущей АВ к
секущей AD, то эта
секущая ближе расположена к касательной
в точке А. Если же уменьшать ∆x
неограниченно, то в пределе секущая
сольется с касательной. Поэтому значение
производной в точке x0
– это тангенс угла наклона касательной
в этой точке, называемый угловым
коэффициентом касательной. При этом
определяется и знак углового коэффициента:
отрицательный знак соответствует
тупому углу наклона секущей к
положительному направлению оси абсцисс.
ассмотренный
выше пример раскрывает физический
смысл производной: если функция выражает
пройденное расстояние в зависимости
от времени, то ее производная – это
скорость. Поясним геометрический смысл
производной. На рисунке отмечены
значения аргумента x0
и x0+∆x
с заданным приращением аргумента ∆x.
Соответствующие значения функции y0
= f(x0)
и f(x0+∆x),
приращение функции ∆y
= f(x0+∆x)
– f(x0).
На графике функции соответствующие
точки обозначены А и В, приращение
аргумента ∆x равно
длине катета АС, а приращение функции
∆y – длине катета ВС
в прямоугольном треугольнике АВС.
Тогда отношение ∆x/∆y
равно тангенсу угла, образованного
секущей АВ с положительным
направлением оси абсцисс. Это отношение
стоит под знаком предела в формуле (3).
Если уменьшить значение ∆x,
на рисунке перейти от секущей АВ к
секущей AD, то эта
секущая ближе расположена к касательной
в точке А. Если же уменьшать ∆x
неограниченно, то в пределе секущая
сольется с касательной. Поэтому значение
производной в точке x0
– это тангенс угла наклона касательной
в этой точке, называемый угловым
коэффициентом касательной. При этом
определяется и знак углового коэффициента:
отрицательный знак соответствует
тупому углу наклона секущей к
положительному направлению оси абсцисс.
Пример 1.2.1.
Пользуясь формулой (3), вычислить
![]() .
.
Решение. Пользуясь формулой «разность синусов», получаем
=![]() =
= =
=
= =
= =
cos x.
=
cos x.
Аналогично можно найти производные от других основных элементарных функций и составить таблицу производных:
 =
0, где с – константа.
=
0, где с – константа. .
.
 ;
;
 .
.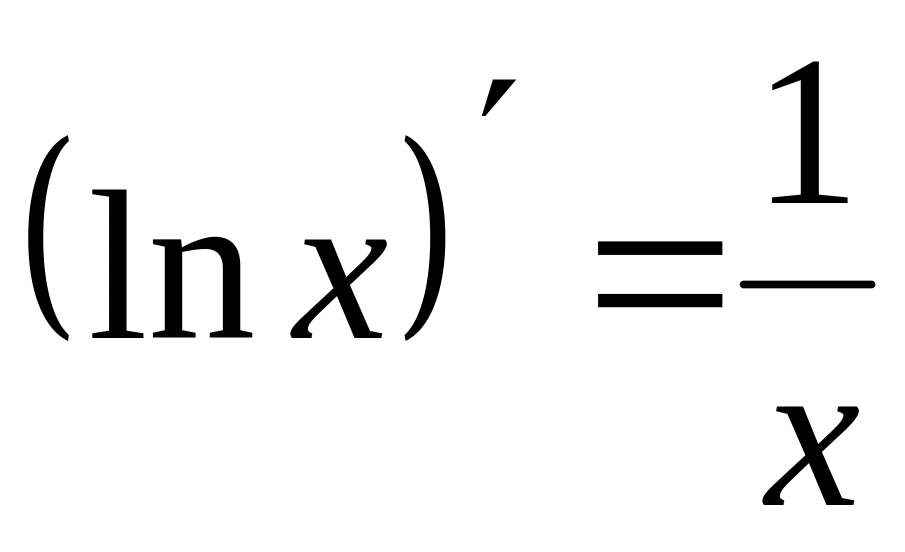 ;
;
 .
. =
cos x.
=
cos x. =
–sin x.
=
–sin x. .
. .
.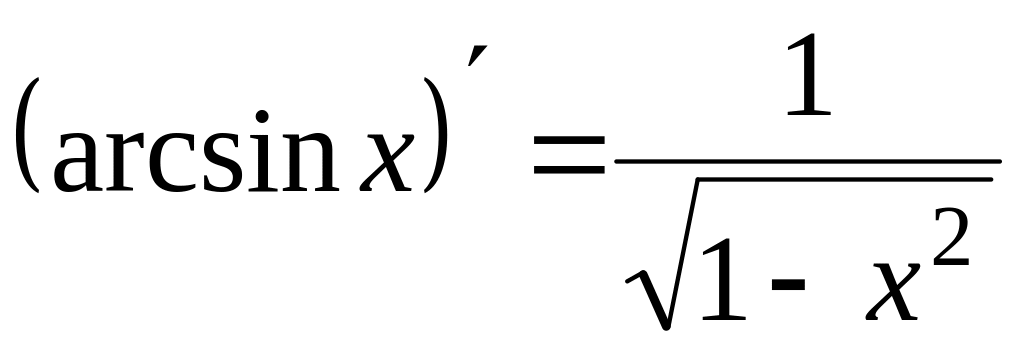 .
. .
. .
. .
.
Нахождение производной называется дифференцированием. Функция, имеющая производную, называется дифференцируемой, а также гладкой.
Для вычисления производных от различных функций пользуемся следующими правилами дифференцирования:
 .
. ,
где с – константа.
,
где с – константа. .
.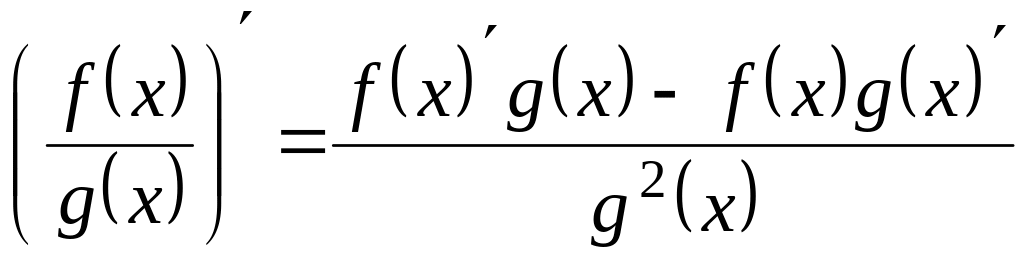 .
. .
.
В последнем правиле
дифференцирования сложной функции
множитель
![]() понимается следующим образом. Берется
производная
понимается следующим образом. Берется
производная
![]() и вместо х в него подставляется
g(x).
Как частный случай из него получаем
следующее правило:
и вместо х в него подставляется
g(x).
Как частный случай из него получаем
следующее правило:
 .
.
Пример 1.2.2.
Продифференцировать следующие
функции: а) x2sinx;
б)![]() ;
в)
;
в)
![]() .
.
Решение.
а)
![]() =
=![]() =
2x sin
x + x2
cos x$
=
2x sin
x + x2
cos x$
б)
![]() =
= =
=![]() =
=![]() ;
;
в)
![]() =
=![]() =
=
=
=![]() =
=![]() .
.
Производную можно использовать при вычислении пределов, когда имеет место неопределенность вида или . Здесь используется:
Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, то есть
![]() .
.
Пример 1.2.2.
Найти предел
![]() .
.
Решение.
=![]() =
=![]() =
=![]() =
1.
=
1.
Производная характеризует
характер монотонности функции. Если
функция f(x)
определена и непрерывна на отрезке [a,
b] и производная
![]() > 0 в интервале (a,
b), то на отрезке
[a, b]
функция строго возрастает. Если же
<0
в интервале (a, b),
то на отрезке [a, b]
функция строго убывает.
> 0 в интервале (a,
b), то на отрезке
[a, b]
функция строго возрастает. Если же
<0
в интервале (a, b),
то на отрезке [a, b]
функция строго убывает.
Производная используется при нахождении экстремумов функций. Для этого находим производную функции. В точках экстремума производная равна 0 или не определена. Находим все нули и точки разрыва производной, это будут точки, подозрительные на экстремум. Если слева и справа от критической точки производная имеет противоположные знаки, то имеем точку экстремума.
