§ 1. Система натуральных чисел

Система натуральных чисел, которую обозначают через N, есть определенное фиксированное множество, элементы которого 1, 2, 3, ... называются натуральными числами. МножествоNобладает следующими свойствами:

1. В Nопределена бинарная алгебраическая операция сложения, которая:

a) коммутативна, т. е. a+b=b+a a, bN;

b) ассоциативна, т. е. (a+b)+c=a+(b+c) a, b, cN.

2. В Nопределена бинарная алгебраическая операция умножения, которая:

a) коммутативна, т. е. ab=ba a, bN;

b) ассоциативна, т. е. (ab)c=a(bc) a, b, cN.

3. Сложение и умножение связаны законом дистрибутивности

(a+b)c=ac+bc a, b, cN.

4. В Nопределено отношение сравнения чисел по величине “aменьшеb” (a<b), при этом выполняются свойства:

a) для любыхa,bNвыполняется одно из соотношенийa<b,b<a,a=b(свойство линейности);

b) соотношениеa<bимеет место тогда и только тогда, когда существует такоеxN, чтоa+x=b(свойство положительности);

c) в любом непустом множествеMNнайдется минимальное число, т. е. такое натуральное числоaM, чтоaxимеет место для всехxM(свойство минимальности);

d) минимальный элемент множестваN, обозначаемый через 1, таков, что для всякогоaNимеет место 1a=a(существование единичного элемента).

Систему Nчасто называют натуральным рядом.

Замечание.Еслиa<b, то говорят: “aменьшеb”, а также “bбольшеa”, “aпредшествуетb”, “bследует заa”. Обозначениеb>aесть другое обозначение дляa<b. Соотношениеabозначает, чтоa<bилиa=b;baесть другое обозначение дляab.

Из основных свойств сложения и умножения вытекают следующие свойства.

1. Свойство сокращения сложения

Если a+x=a+y, то x=y.

Действительно, допустим, что xy, тогда, по свойству линейности, илиx<y, илиy<x. Пустьx<y, тогда существуетzNтакое, чтоx+z=y, следовательно,a+x=a+y=a+(x+z)=(a+x)+z. Из того, чтоa+y=(a+x)+z, следует, чтоa+x<a+y, чего быть не может. Аналогично получим противоречие, если полагать, чтоy<x.

2. Свойство сокращения умножения

Если ax=ay, то x=y.

Действительно, допустим, что xy. Не нарушая общности рассуждения, можно полагать, чтоx<y, тогдаx+z=y, а потомуax=ay=a(x+z)=ax+az. Из того чтоay=ax+az, следует, чтоax<ayвопреки тому, чтоax=ay. Предположение о том, чтоxy, неверно.

3. Свойство транзитивности

Если a<bиb<c, тоa<c.

Из условия следует, что b=a+zиc=b+u, тогдаc=b+u=(a+z)+u=a+(z+u)=a+v. Отсюда следует, что a<c.

4. Стабильность сложения

Для всех a,b,cN, еслиa<b, тоa+c<b+c.

Действительно, если a<b, тоb=a+x. Но тогда

b+c=(a+x)+c=a+(x+c)=(a+c)+x.

Отсюда a+c<b+c.

5. Стабильность умножения

Для всех a,b,cNеслиa<b, тоac<bc. Действительно, еслиa<b, тоb=a+x. Но тогдаbc=(a+x)c=ac+cx. Отсюда ac<bc.

6. Если a1, то ab>b, a, bN.

Так как a1, тоa>1, тогдаab>1b.

7. Свойство Архимеда

Для любых a,bNсуществуетnNтакое, чтоna>b.

Действительно, в качестве nможно взять любое натуральное число, большееb. Пустьn=b+1. Так какa1, тоna=(b+1)a>b, т. е.na>b.

Значение.В свойствах 3, 4, 5 вместо<можно взять.

§ 11. Метод математической индукции

Метод математической индукции играет существенную роль в матема­тических доказательствах. Многие утверждения без указанного метода дока­зать просто невозможно.

Поскольку в методической литературе часто встречаются такие понятия, как полная индукция, неполная индукция и метод математической индукции, то начнем с их определения.

Полная индукция

По своему первоначальному смыслу слово «индукция» применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частых утверждений. Простейшим методом рассуждений такого рода является полная индукция. Суть ее состоит в том, что общее утверждение доказывается рассмотрением всех возможных случаев.

Например, известно, что имеется пять типов правильных многогран­ников.

1. Тетраэдр. В каждой вершине сходятся 3 ребра. Имеет 4 грани (треугольные), 6 ребер, 4 вершины. Тетраэдр является правильной треуголь­ной пирамидой (рис. 1).

Рис. 1

2. Куб. В каждой вершине сходятся 3 ребра. Имеет 6 граней (квадратные), 12 ребер, 8 вершин (рис.2).

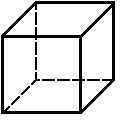
Рис. 2

3. Октаэдр. В каждой вершине сходятся 4 ребра. Имеет 8 граней (треугольных), 12 ребер, 6 вершин (рис. 3).

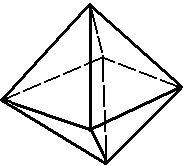
Рис. 3

4. Икосаэдр. В каждой вершине сходятся 5 ребер. Имеет 20 граней (треугольных), 30 ребер, 12 вершин (рис. 4).

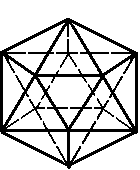
Рис. 4

5. Додекаэдр. В каждой вершине сходятся 3 ребра. Имеет 12 граней (пятиугольных), 30 ребер, 20 вершин (рис. 5).

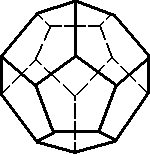
Рис. 5

Обозначим через Г  число граней, Р  число ребер, В  число вершин. Имеет место утверждение: "Для пяти типов правильных многоугольников имеет место соотношение Г+В=Р+2".

Тетраэдр Куб Октаэдр Икосаэдр Додекаэдр

4 + 4 = 6 + 2 6 + 8 =12 + 2 8 + 6 = 12 + 2 20 + 12 = 30 + 2 20 + 12 = 30 + 2

Утверждение доказано полной индукцией.

Пример. Доказать, что любое четное натуральное число 4n16 представимо в виде суммы двух простых чисел. Действительно,

4=2+2, 6=3+3, 8=3+5, 10=5+5, 12=5+7, 14=7+7, 16=5+11.

Тем самым утверждение доказано.