Модуль 4.

Элементы комбинаторики

Темы 6, 7.

Элементы комбинаторики. Понятие о комбинаторной задаче. Соединения без повторений.

Соединения с повторениями.

Цель изучения темы: введение фундаментальных понятий математики, связанных с основными видами соединений без повторений и с повторениями, формирование умений использовать простейшие правила комбинаторики.

План:

1. Понятие о комбинаторной задаче.

2. Правило суммы и правило произведения.

3. Соединения без повторений и с повторениями состава.

Основная литература по теме

1. Стойлова, Л. П. Математика / Л. П. Стойлова.- М.: Изд. центр «Академия», 2007. – 432 с.

Дополнительная литература

1. Популярные лекции по математике. Московский Центр непрерывного математического образования при поддержке Издательства "Физматлит". [Электронный ресурс] / Режим доступа: http://ilib.mirror1.mccme.ru/plm/- Загл. с экрана. Выпуск 45.

На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т. д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют «комбинаторные задачи».

Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества. Термин «комбинаторика» происходит от латинского combina – сочетать, соединять.

Комбинаторика – область математики, в которой рассматриваются задачи о тех или иных комбинациях объектов. Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Несмотря на свою простоту и наглядность, комбинаторные задачи очень трудны, многие из них остаются нерешенными сотни лет.

Комбинаторная задача – задача, в которой идет речь о тех или иных комбинациях объектов.

Очень большое количество реальных задач - задачи переборные и только для некоторых найдены способы избегать перебора.

Пример 1.

Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок (белой, синей, красной)? Есть ли в мире государства, где встречаются те же цвета полосок?

Подсчитать число вариантов флагов с горизонтально расположенными полосками нетрудно. Но надо учесть, что встречаются флаги и с другим расположением полосок.

Комбинаторными являются и многие геометрические задачи и задачи с дробями.

Пример 2. В фигуре, изображенной на рисунке, переложить 5 спичек так, чтобы всего получилось 2 квадрата.

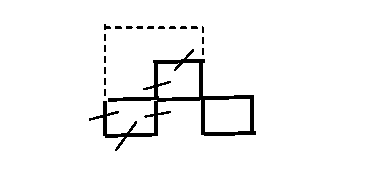
Рис.1

Пример 3. Можно ли разделить поровну 5 пряников между шестью мальчиками, не разрезая ни одного пряника на 6 равных частей?

Пример 4. Приведем задачу, которую придумал Л.Н. Толстой: «Косцы должны скосить 2 луга. С утра они все вместе стали косить большой луг. По происшествие половины рабочего дня косцы разделились: половина их осталась на большом лугу и к вечеру его докосили, а другая половина перешла косить другой луг, вдвое меньший первого, но не успела к концу дня закончить косьбу. На другой день на этот луг вышел один косец и в течение всего дня докосил его. Сколько всего было косцов?»

Пример 5. Приведем старинную комбинаторную задачу, которую придумал И. Ньютон и сформулировал в виде стихотворения. В переводе на русский язык она звучит так: «Мне нужна Ваша помощь, чтобы посадить девять деревьев в десять рядов так, чтобы в каждом ряду было три дерева. Скажи – как, и я ничего больше не спрошу».

Введем понятие кортежа (упорядоченной n-ки элементов).

Кортеж – конечная упорядоченная последовательность (допускающая повторения) элементов какого-нибудь множества. Длиной кортежа называется число элементов в нем.

Самым простым примером является упорядоченная пара – кортеж длины 2.

Решая ту или иную комбинаторную задачу, необходимо проанализировать, важен ли порядок в тех соединениях элементов, число которых мы ищем.

Приведем некоторые правила, лежащие в основе комбинаторных задач.

Если некоторый объект А может быть выбран из совокупности объектов k способами, а другой объект В может быть выбран s способами, то выбрать либо А, либо В можно k + s способами. Это простейший вариант так называемого правила суммы.

Правило суммы: пусть имеется n попарно непересекающихся множеств A₁, A₂, …, A_n, содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно

m₁ + m₂ + … + m_n.

Правило произведения: пусть имеется n множеств A₁, A₂, …, A_n содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а₁, а₂, ..., а_n), где а_i  А_i (i = 1, 2, …, n), равно

m₁ ּ m₂ ּ … ּ m_n .

Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.

Размещения без повторений (n различных элементов):

.

Эта формула применяется тогда, когда ставится вопрос о числе упорядоченных подмножеств, содержащих m элементов множества, состоящего из n элементов. Здесь условие m≤ n является обязательным.

Размещения с повторениями (n различных элементов, элементы могут повторяться):

Эта формула применяется тогда, когда также ставится вопрос о числе упорядоченных подмножеств, содержащих m элементов множества, состоящего из n элементов. Но здесь условие m≤ n не является обязательным, т.е. элементы кортежа могут повторяться.

Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться?

1) Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.

.

2) Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.

Перестановками из n элементов называются размещения из этих n элементов по n. Перестановки – частный случай размещений.

Перестановки без повторений (n различных элементов):

Эта формула применяется при решении тех задач, где ищется число способов упорядочения множества, содержащего n элементов.

Перестановки c повторениями (k различных элементов, где элементы могут повторяться m₁, m₂, …, m_k раз и m₁ + m₂ + … + m_k = n, где n – общее количество элементов):

Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?

1) Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.

2) Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.

Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом.

Отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов.

Сочетания без повторений (n различных элементов, взятых по m):

.

Здесь порядок не является существенным, речь идет о совокупностях и условие m≤ n является обязательным.

Сочетания c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться):

.

Здесь порядок также не является существенным, речь идет о совокупностях, но m≤ n не является обязательным.

Пример. Возьмем плоды: банан (Б), ананас (А) и репа (Р). Какие сочетания из этих плодов, взятых по два, можно получить? Сколько таких наборов получится, если: 1) плоды в наборе не повторяются; 2) можно брать по два одинаковых плода?

1) Получатся наборы: БА («банан, ананас» и «ананас, банан» – один и тот же набор), АР и РБ.

.

2) Получатся наборы: ББ, БА, БР, АА, АР, РР.

.