
- •Математический анализ
- •1.Пределы
- •2.Элементы дифференциального исчисления
- •1. Производная
- •2. Дифференциал
- •3. Производные высших порядков
- •4. Исследование функций
- •3.Элементы интегрального исчисления
- •1. Неопределенный интеграл
- •2. Определенный интеграл
- •4.Функции нескольких переменных
- •1. Частные производные
- •2. Кратные интегралы
- •6.Дифференциальные уравнения
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения
Математический анализ
1.Пределы
Рассмотрим бесконечную
числовую последовательность (a1,
a2, … , an,
…). Сокращенно ее можно обозначить
![]() или просто (an).
Попытаемся сформулировать определение
предела последовательности. В качестве
примера рассмотрим три последовательности:
или просто (an).
Попытаемся сформулировать определение
предела последовательности. В качестве
примера рассмотрим три последовательности:
1, 2, 3, … , n, … (1)
1,
![]() ,
,
![]() ,
… ,
,
… ,
![]() ,
… (2)
,
… (2)
1, –1, 1, –1, … , (–1)n+1, … (3)
На интуитивном уровне понятно, что первая последовательность не имеет предела, вторая имеет пределом число 0. Последнее проявляется в том, что члены последовательности (2) с увеличением номера n все ближе подбираются к 0. Но к числу –1 они тоже становятся все ближе. Принципиальная разница в том, что к 0 они могут подойти как угодно близко, а расстояние до –1 не может стать меньше 1. Оборот «как угодно близко» означает, например, что расстояние от an до 0 можно сделать меньше 0,1, если взять n > 10, или меньше 0,001, если взять n > 1000; и вообще, какое бы малое положительное число ни взять, найдется такой номер N, после которого все члены последовательности будут отстоять от 0 ближе, чем на .
Мы подошли к точному определению предела последовательности.
Число а называется пределом последовательности (an) (записывается
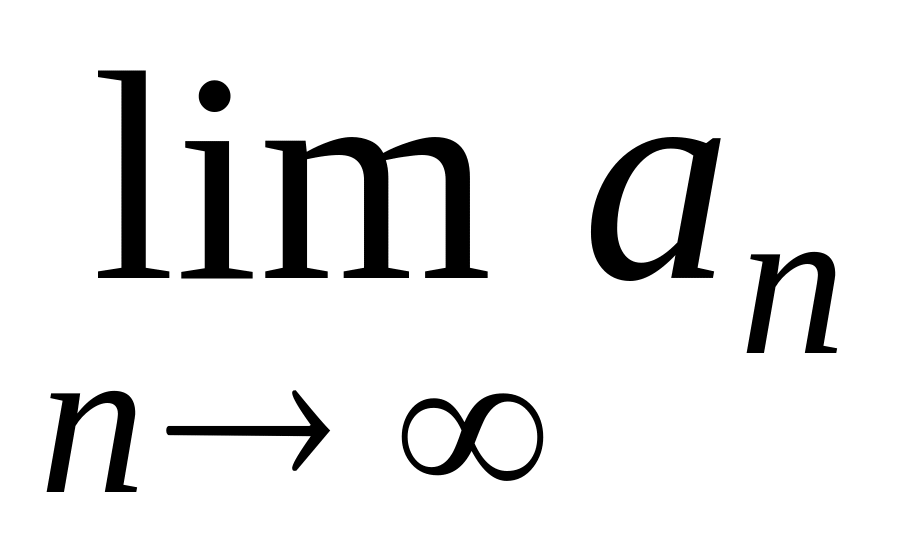 =
а, читается «предел an
при n, стремящемся
к бесконечности, равен а»), если для
любого положительного числа
найдется такое число N,
зависящее от , что
an
– а <
при всех n > N.
=
а, читается «предел an
при n, стремящемся
к бесконечности, равен а»), если для
любого положительного числа
найдется такое число N,
зависящее от , что
an
– а <
при всех n > N.
Последовательность, имеющая предел, называется сходящейся, не имеющая предела – расходящейся.
В соответствии с определением предела заключаем, что последовательности (2) и (3) предела не имеют. Но их поведение различное. Члены последовательности (2) неограниченно возрастают, и в этом случае можно сказать, что = . Члены последовательности (3) концентрируются около двух точек 1 и –1. Эти точки называются предельными точками последовательности.
Условие = а можно сформулировать равносильным образом: an → а при n → .
При вычислении пределов используются их основные свойства:
![]() ;
;
![]() ;
;
![]() ;
;
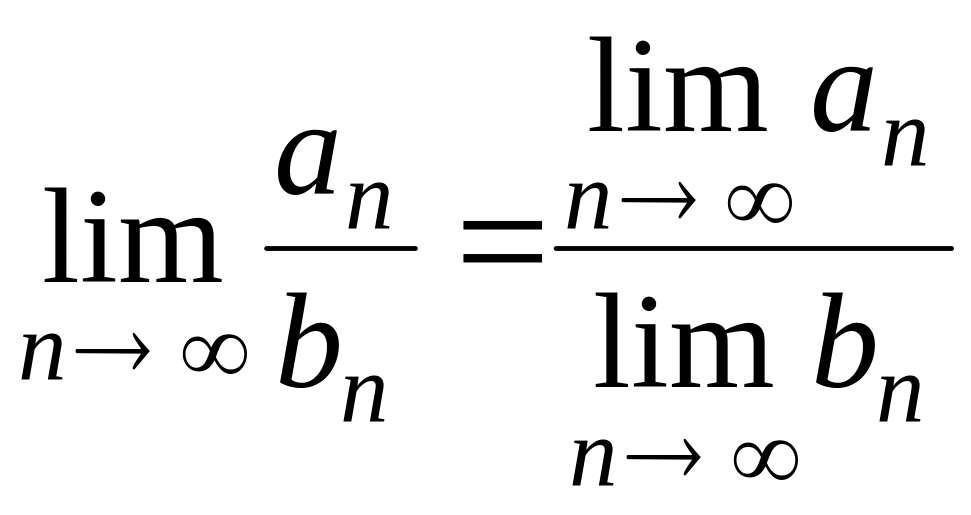 .
.
При этом должны существовать все пределы в правых частях этих равенств.
Для вычисления предела
последовательности определяющими
являются понятия бесконечно малой
и бесконечно большой величин: это
соответственно последовательности,
стремящиеся к 0 и к бесконечности.
Соотношение между ними такое: если an
→ 0, то
![]() →
, и an
→ , то
→
0. При этом в числителе может стоять
любое число, не равное 0. Условно эти
соотношения записывают в виде
→
, и an
→ , то
→
0. При этом в числителе может стоять
любое число, не равное 0. Условно эти
соотношения записывают в виде
![]() ,
,
![]() .
С их помощью можно найти простые пределы,
например,
.
С их помощью можно найти простые пределы,
например,
![]() .
.
Более сложные случаи –
неопределенности вида
![]() .
При вычислении соответствующих пределов
от таких неопределенностей следует
избавляться, как показано в следующих
примерах.
.
При вычислении соответствующих пределов
от таких неопределенностей следует
избавляться, как показано в следующих
примерах.
Пример 1.1.1. Вычислить
пределы: а)
![]() ;
б)
;
б)
![]() .
.
Решение.
а)
=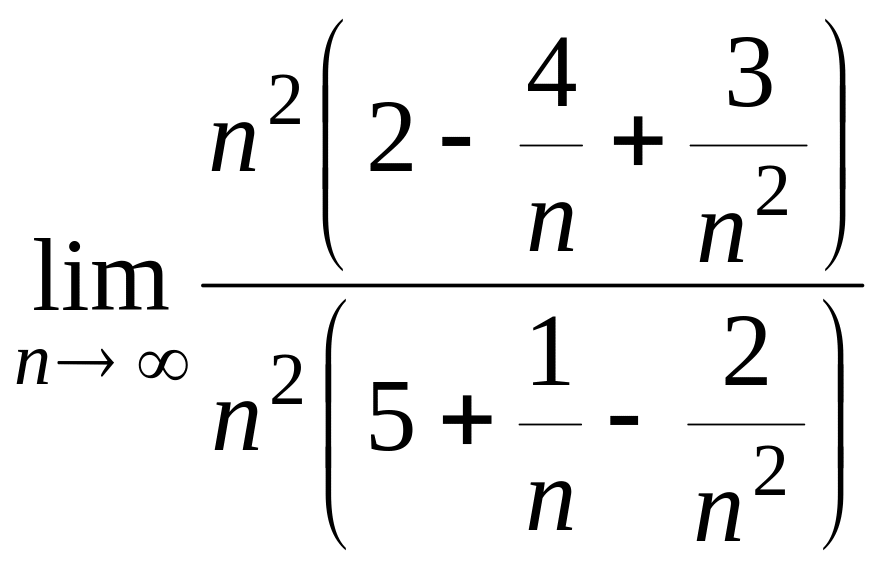 =
=
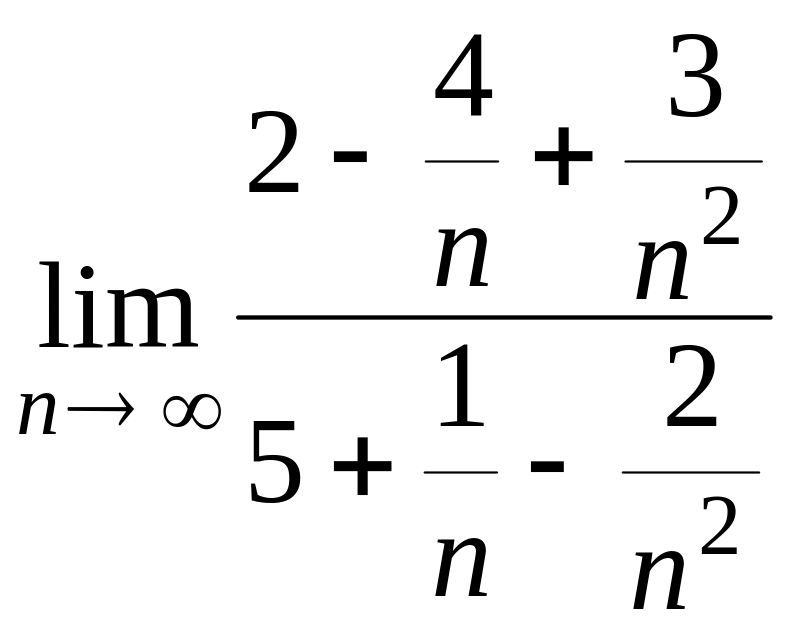 =
=
=
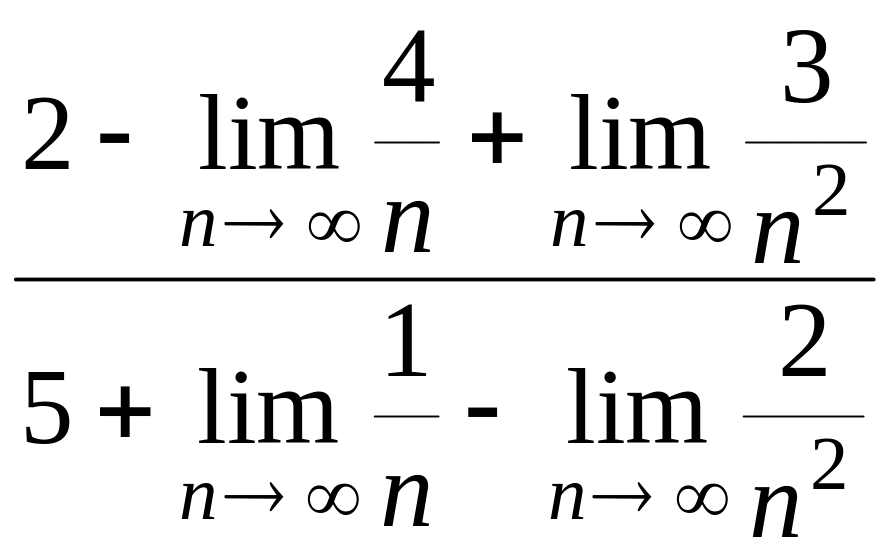 =
=![]() ;
;
б)
=
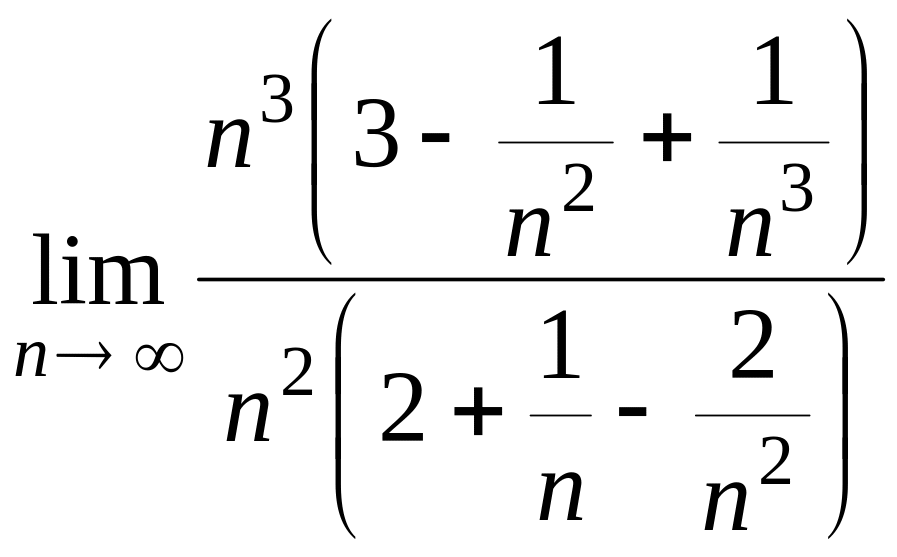 =
=
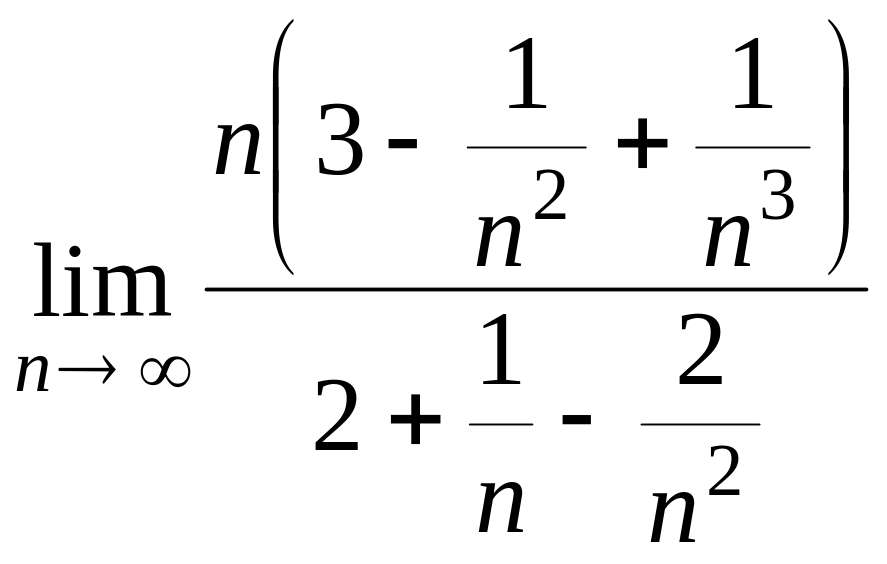 =
.
=
.
При вычислении этих пределов мы пользовались свойствами, сформулированными выше. Во втором примере опущены подробности.
Рассмотрим теперь понятие
предела функции. На рис.1 показаны
различные случаи расположения графика
функции y = f(x).
Нас интересует поведение функции y,
когда переменная х стремится к а.
На рисунках а) и б) видно, что при
этом значения y
стремятся к b, причем
на рисунке а) это и есть f(а),
а на рисунке с) значение f(а)
= с отличается от b.
Но в обоих этих случаях мы говорим, что
![]() =
b. Понятно, что на
рисунках в) и г)
не существует.
=
b. Понятно, что на
рисунках в) и г)
не существует.
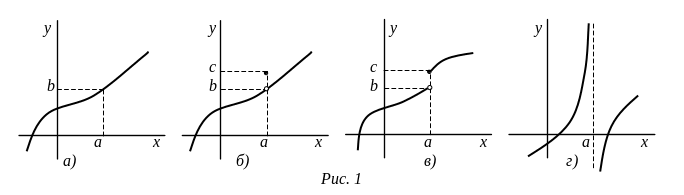
В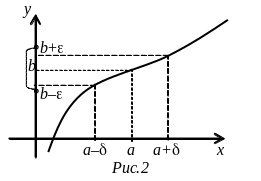 чем же проявляется тот факт, что
=
b на рис. а) и b)?
В том, что значения f(x)
можно сделать как угодно близкими к b,
если значения х сделать достаточно
близкими к а. Точный смысл оборота
«как угодно близкими» в том, что какое
бы малое значение
ни задать, значение f(x)
– b
можно сделать меньше ,
выбрав подходящим образом область
значений для х. Условие f(x)
– b<
равносильно двойному
неравенству b –
< f(x)
< b + ,
то есть f(x)
принадлежит интервалу (b
– , b
+ ). Такой интервал
называется -окрестностью
точки b: эта точка
является центром интервала,
задает его ширину. Выбранная область
значений для х также должна
представлять собой некую -окрестность
точки а, то есть для ее задания нужно
подобрать подходящее значение .
Связь между и
проиллюстрирована на рис.2. -окрестность
точки b выделена на
оси ординат скобкой, определенная для
нее -окрестность
точки а выделена на оси ординат
жирной линией. Значения аргумента х
из -окрестности
точки а расположены между двумя
крайними штриховыми линиями на оси
абсцисс, соответствующие значения
функции расположены между двумя крайними
штриховыми линиями на оси ординат, –
все они попали в -окрестность
точки b. При этом
значение можно
было выбрать меньше или даже чуть больше
представленного, это не принципиально;
важно, что такое значение существует.
чем же проявляется тот факт, что
=
b на рис. а) и b)?
В том, что значения f(x)
можно сделать как угодно близкими к b,
если значения х сделать достаточно
близкими к а. Точный смысл оборота
«как угодно близкими» в том, что какое
бы малое значение
ни задать, значение f(x)
– b
можно сделать меньше ,
выбрав подходящим образом область
значений для х. Условие f(x)
– b<
равносильно двойному
неравенству b –
< f(x)
< b + ,
то есть f(x)
принадлежит интервалу (b
– , b
+ ). Такой интервал
называется -окрестностью
точки b: эта точка
является центром интервала,
задает его ширину. Выбранная область
значений для х также должна
представлять собой некую -окрестность
точки а, то есть для ее задания нужно
подобрать подходящее значение .
Связь между и
проиллюстрирована на рис.2. -окрестность
точки b выделена на
оси ординат скобкой, определенная для
нее -окрестность
точки а выделена на оси ординат
жирной линией. Значения аргумента х
из -окрестности
точки а расположены между двумя
крайними штриховыми линиями на оси
абсцисс, соответствующие значения
функции расположены между двумя крайними
штриховыми линиями на оси ординат, –
все они попали в -окрестность
точки b. При этом
значение можно
было выбрать меньше или даже чуть больше
представленного, это не принципиально;
важно, что такое значение существует.
Мы подошли к точному определению предела функции.
Число b называется пределом функции f(x) в точке а, если для любого положительного числа найдется такое число , зависящее от , что f(x) – b< при x – а< .
На рис. 1с) предел в точке а не существует: если взять < c – b, то в -окрестность точки b не попадут значения f(x), когда х > a: значения f(x) будут больше с и вылезут за пределы -окрестность точки b. Значит, подходящую -окрестность точки а подобрать невозможно, и b не может быть пределом функции. Аналогично с не может быть пределом функции. В этом случае можно говорить об односторонних пределах функции f(x) в точке а: левый предел равен b, правый – с.
Рассматривается
также предел
![]() ,
а также отдельно
,
а также отдельно
![]() и
и
![]() (точные определения опускаем).
(точные определения опускаем).
При вычислении пределов функции используются такие же свойства, как для пределов последовательности.
Самый простой случай вычисления предела функции имеет место, если допускается непосредственная подстановка.
Пример 1.1.2.
![]() =
=![]() =
=![]() .
.
Если же в
результате подстановки получается
неопределенность вида
,
или
![]() ,
или другая, то применяются специальные
приемы для снятия этих неопределенностей.
С неопределенностью вида
поступаем обычно как при вычислении
пределов последовательностей. Рассмотрим
приемы снятия неопределенности вида
.
,
или другая, то применяются специальные
приемы для снятия этих неопределенностей.
С неопределенностью вида
поступаем обычно как при вычислении
пределов последовательностей. Рассмотрим
приемы снятия неопределенности вида
.
Пример 1.1.3.
Вычислить
![]() .
.
Решение. При непосредственной подстановке получаем неопределенность вида . В числителе и знаменателе дроби стоят многочлены. Число 2 является корнем каждого из них. Это значит, что каждый многочлен разлагается в произведение двух множителей, один из которых равен (х – 2). Имеем
=![]() =
=![]() =
=![]() = –1.
= –1.
Здесь мы произвели сокращение на (х – 2). Это не есть сокращение на 0, так как это выражение равно 0 только при х = 2, а мы анализируем значения функции вблизи точки 2, в самой этой точке значение не рассматривается.
Пример 1.1.3.
Вычислить
![]() .
.
Решение. При непосредственной подстановке получаем неопределенность вида . В знаменателе дроби многочлен, у него выделяется множитель (х – 1). Чтобы поступить подходящим образом с числителем, преобразуем его в многочлен, домножив на сопряженное выражение:
=
![]() =
=
![]() = =
= =![]() =
=![]() =
=![]() =
=![]() .
.
При снятии неопределенности вида , когда присутствуют тригонометрические выражения, может использоваться первый замечательный предел:
![]() =
1.
=
1.
Пример 1.1.4.
![]() =
=
![]() =
=![]() =
=
![]() .
.
При снятии неопределенности
вида
![]() обычно используется второй замечательный
предел:
обычно используется второй замечательный
предел:
![]() = e,
= e,
или
![]() =
e.
=
e.
Пример 1.1.5.
![]() =
=![]() =
=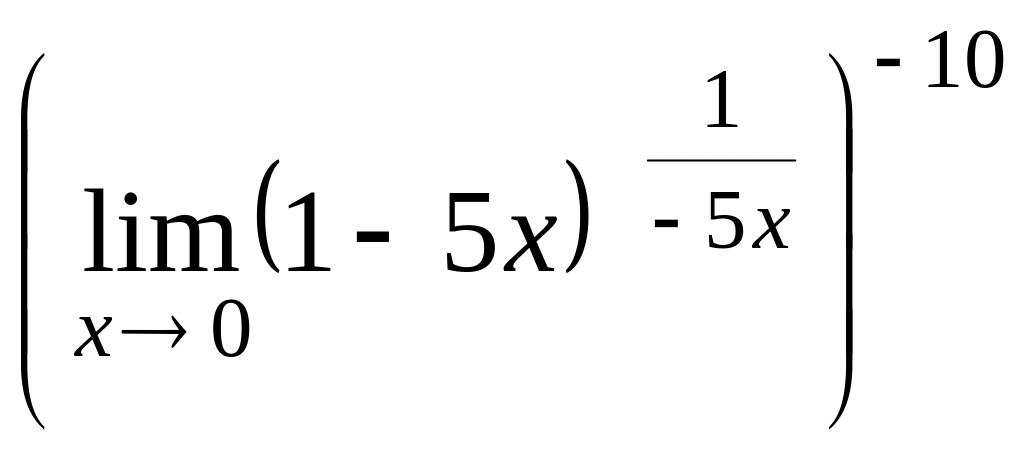 =
е-10.
=
е-10.
Здесь приведены самые элементарные приемы вычисления пределов. Другие способы используют, например, понятие эквивалентного выражения, правило Лопиталя.
С понятием предела тесно связано понятие непрерывности.
Функция f(x) называется непрерывной в точке а, если = f(а). Функция называется непрерывной в промежутке, если она непрерывна в каждой точке этого промежутка.
Точка, в которой функция не является непрерывной, есть точка разрыва функции при условии, что функция определена в некоторых промежутках, примыкающих к этой точке слева и справа. В самой точке разрыва функция может быть и не определена. На рис.1 б), в) и г) точка а является точкой разрыва. При этом на рис.1 б) существует , но он не равен f(а). На рис.1 в) существуют левый и правый пределы, не равные друг другу. На рис.1 г) не существует. Это различные виды разрывов, но бывают и более сложные разрывы.
Функция называется кусочно непрерывной, если ее область определения разбивается на несколько (конечное число) промежутков, в каждом из которых функция непрерывна. Такой же смысл имеют другие кусочные свойства, которые будут использоваться ниже.
У п р а ж н е н и я
1.1.1. Вычислить пределы:
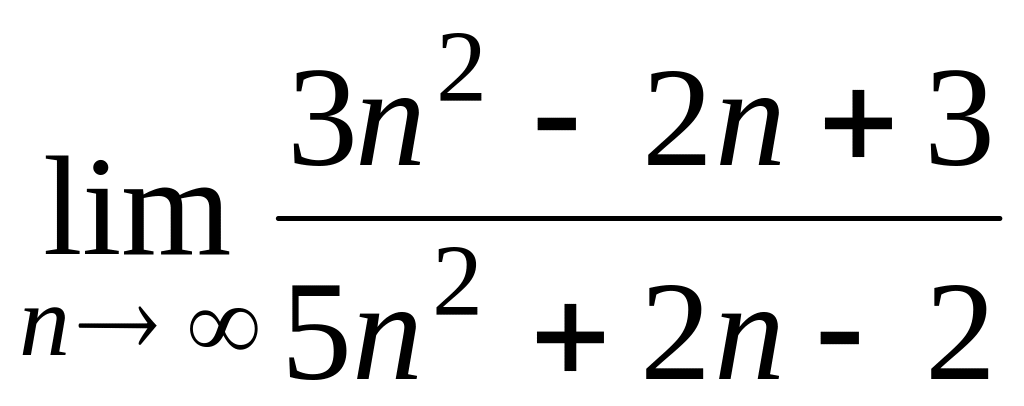 ;
;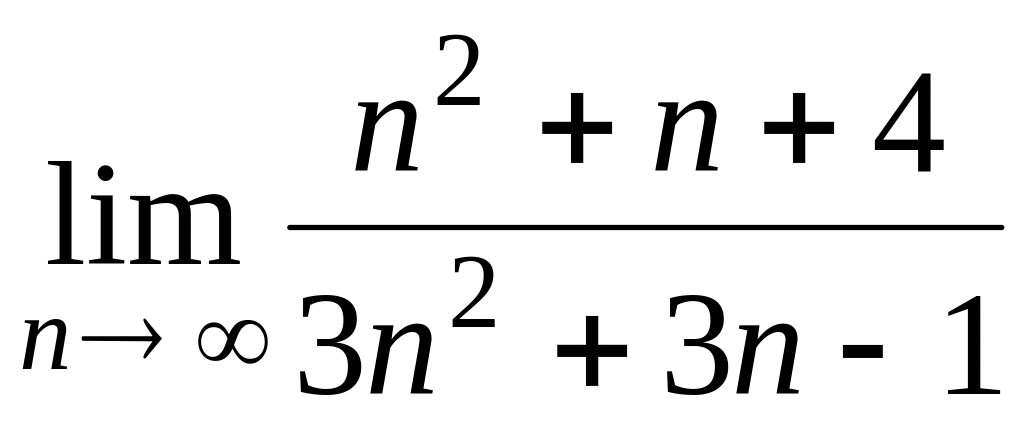 ;
;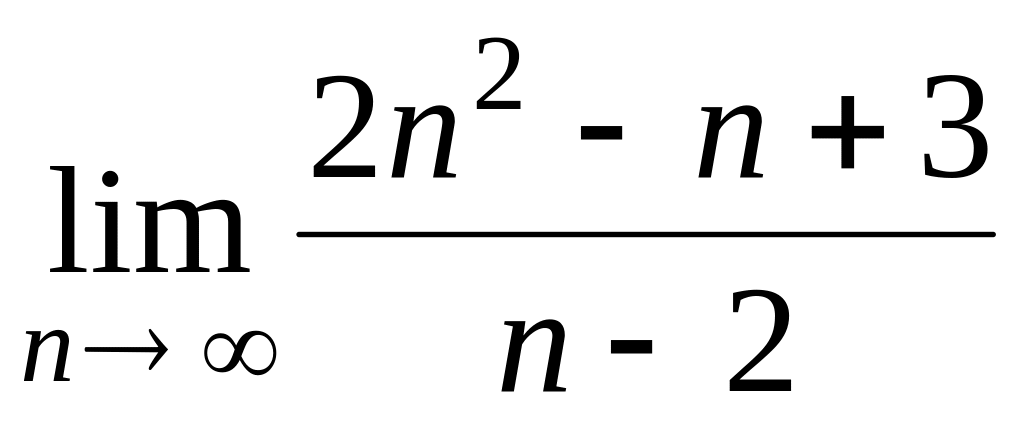 ;
;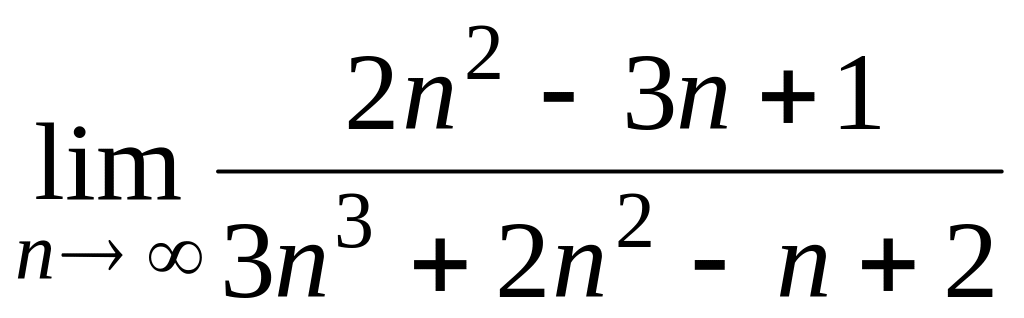 ;
;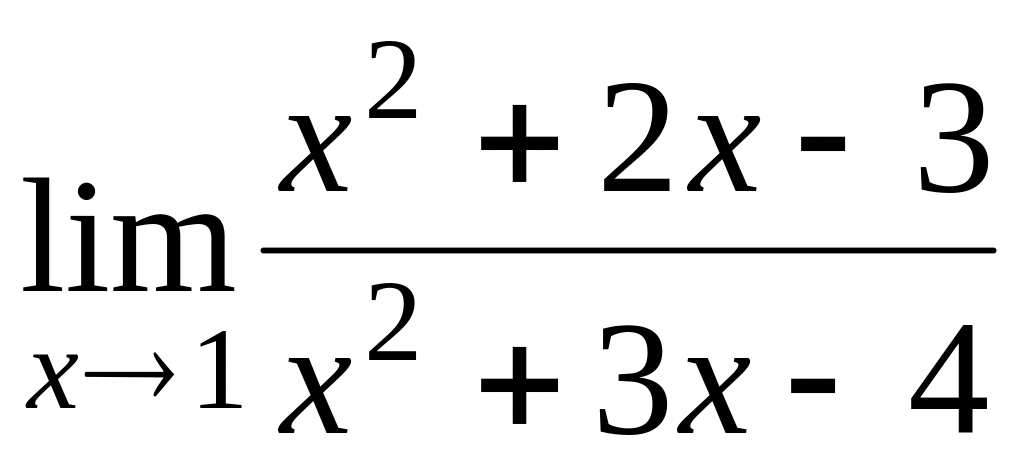 ;
;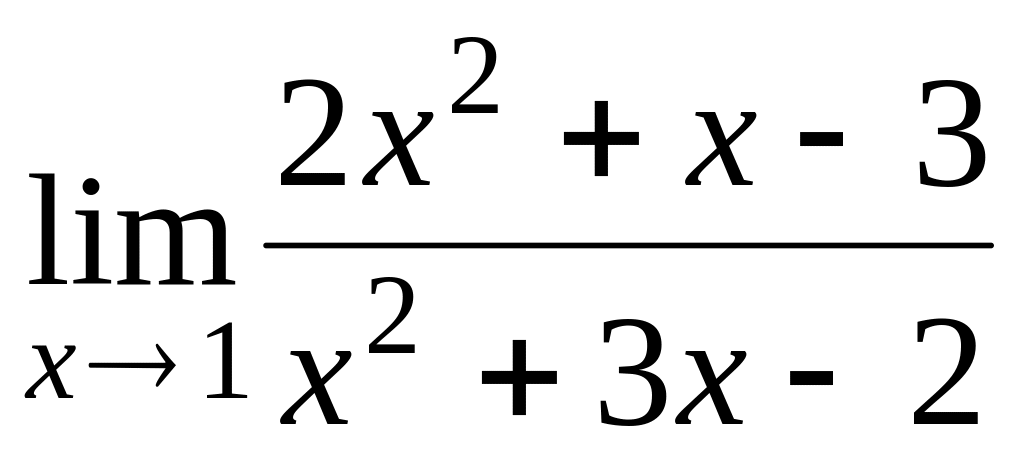 ;
;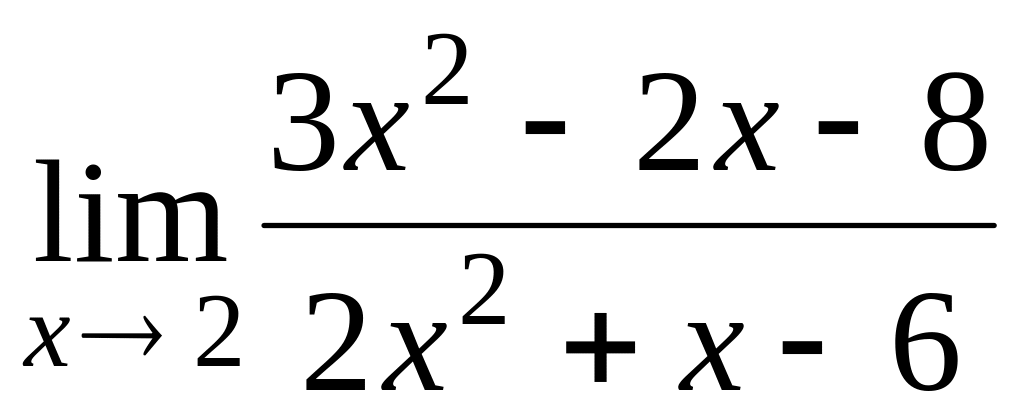 ;
;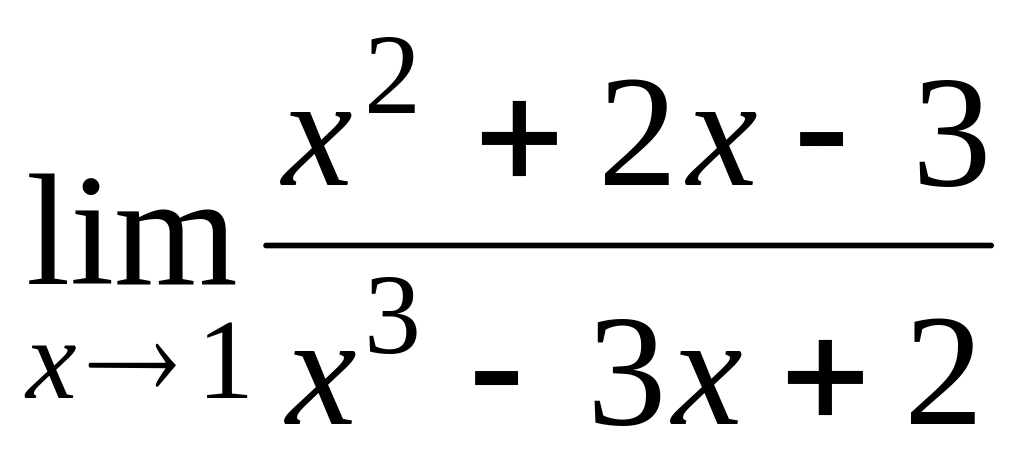 ;
;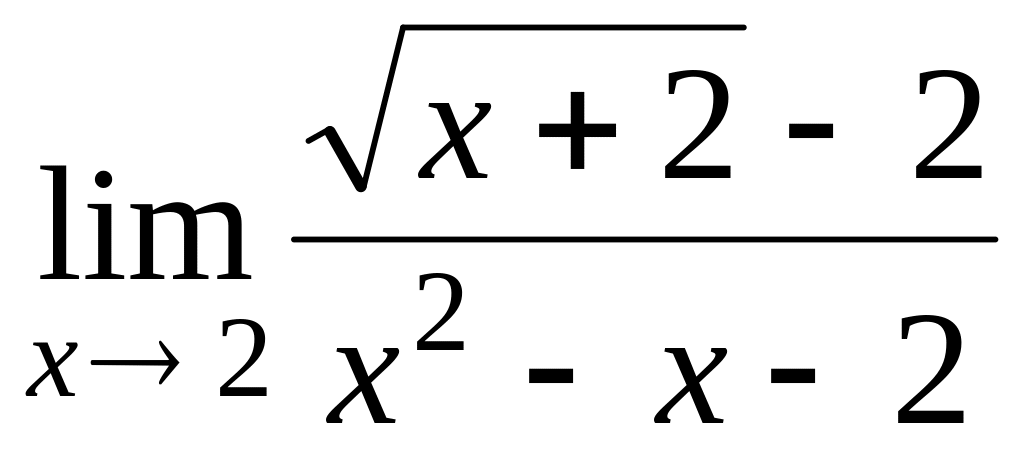 ;
;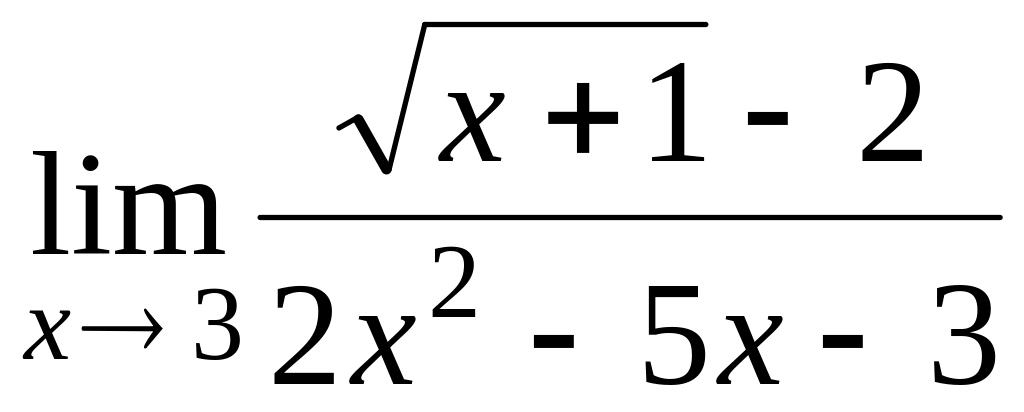 ;
; ;
; ;
;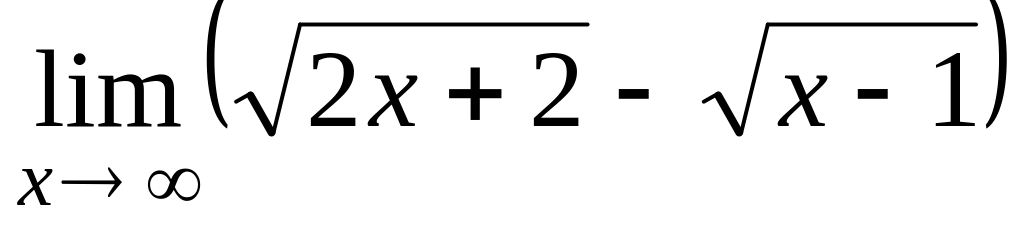 ;
;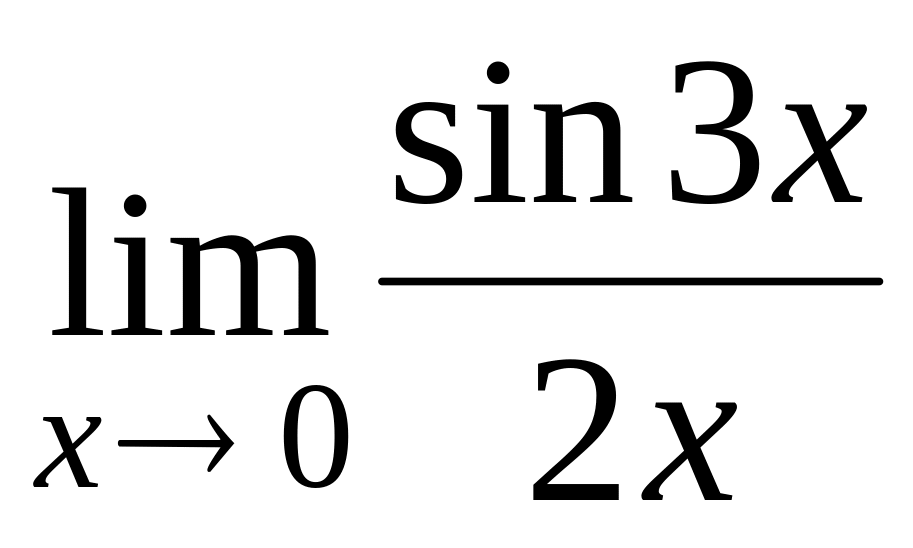 ;
;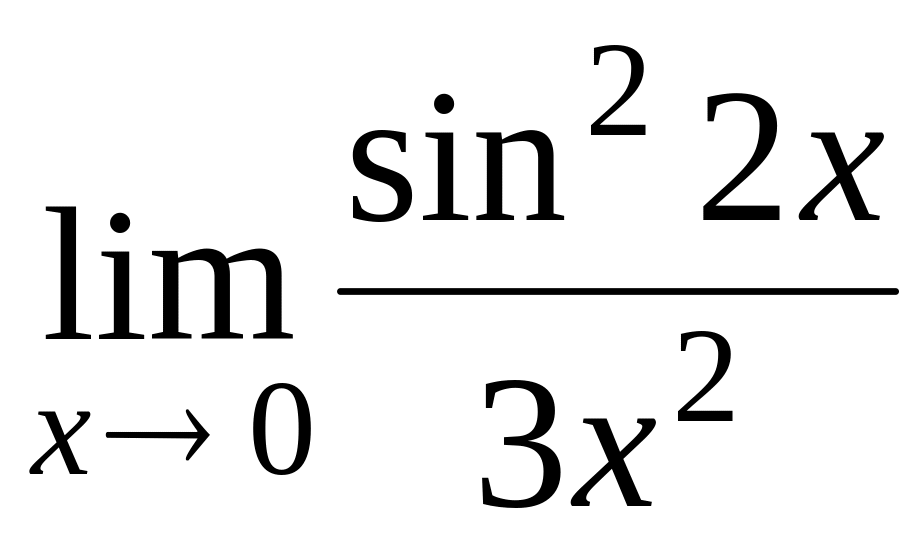 ;
; ;
;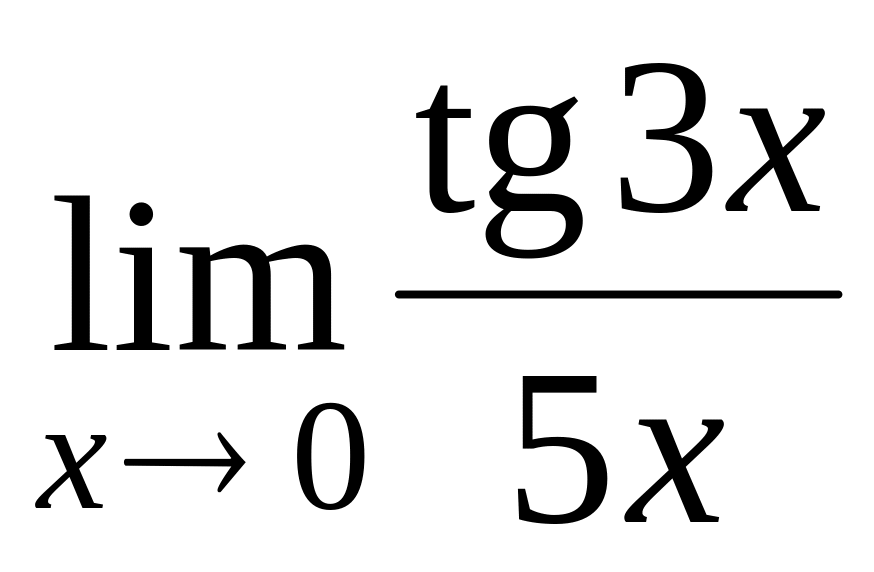 ;
; ;
;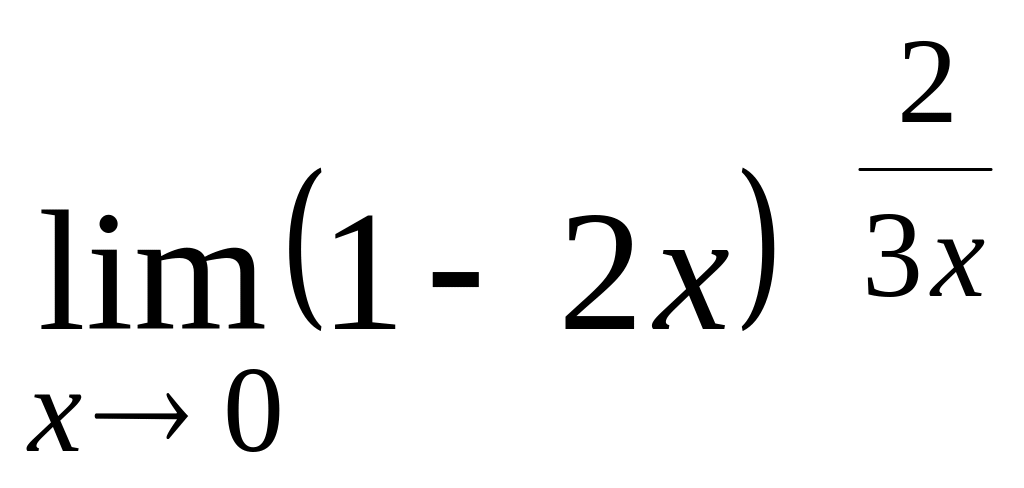 ;
;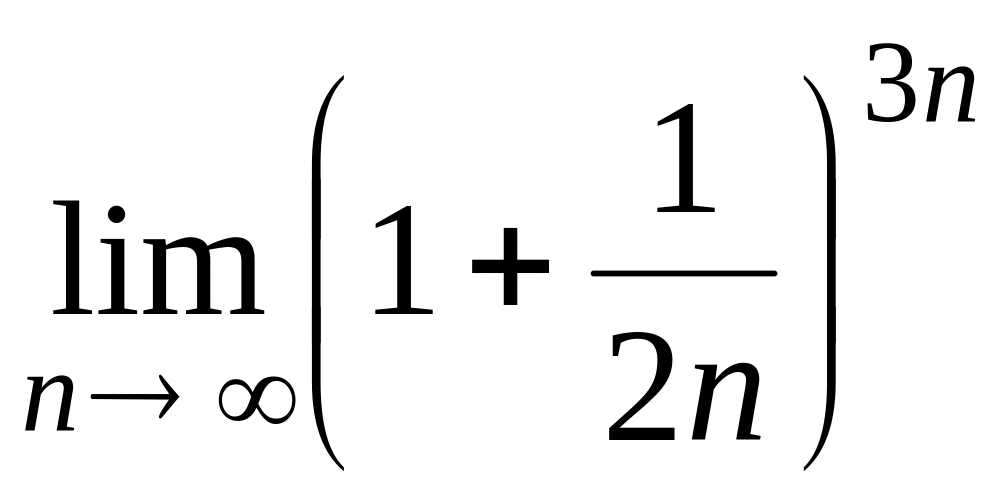 ;
; .
.
