2. Дифференциал

Формулу (3) для вычисления производной можно записать в виде . В числителе и знаменателе стоят приращения функции и аргумента. С понятием приращения тесно связано понятие дифференциала. Дифференциал аргумента dx совпадает с его приращением, dx = ∆x, это бесконечно м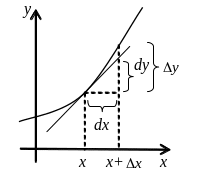 алая величина. Дифференциал функции – это главная часть ее приращения. Он является приращением ординаты касательной к данной функции в точке х. На рисунке видно, что чем меньше ∆x, тем меньше относительная разница между dx и ∆x.

Так как значение производной в точке х – это угловой коэффициент наклона касательной в этой точке, то получаем соотношение

dy = dx.

Отсюда получаем

.

Поэтому производную часто обозначают .

Дифференциал может применяться в приближенных вычислениях.

Пример 1.2.3. Найти приближенное значение .

Решение. Введем функцию y = . Полагаем х₀ = 8, ∆x = 0,03. Тогда y₀ = = 2, и надо найти ∆y. Пользуемся приближенным равенством ∆y = dy. Вычисляем последовательно

;

;

∆y ≈ dy = (x₀) dx = = 0,0025;

y = y₀ + ∆y ≈ 2 + 0,0025 = 2,0025.

Если воспользоваться калькулятором, получим = 2,002497, то есть результат оказался очень точным.

3. Производные высших порядков

Производная от данной функции f(x) сама является функцией. Если она дифференцируема, то ее производная называется производной второго порядка, или второй производной от функции f(x) и обозначается . Аналогично можно рассматривать третью производную , и т.д. Дальнейшие производные обозначаются римскими цифрами, например, , или арабскими цифрами в скобках: – производная n-го порядка.

Е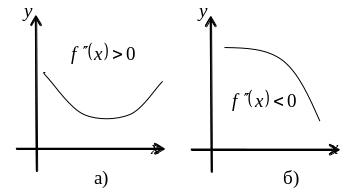 сли первая производная позволяет оценивать характер монотонности функции, то вторая производная характеризует ее выпуклость. На рисунке а) показана функция, выпуклая вниз, или просто выпуклая, а на рисунке б) – выпуклая вверх, или вогнутая. Вторая производная для этих функция соответственно положительная и отрицательная. Запомнить это условие позволяет правило дождя: представляем, что идет дождь. График функции рассматриваем как чашу. Положительная вторая производная означает, что дождь собирается в чашу, то есть ее дно направлено вниз; при отрицательной второй производной дождь не собирается, дно чаши направлено вверх.

Точка графика, в которой выпуклость меняется на вогнутость или наоборот, называется точкой перегиба (при условии, что функция в этой точке гладкая). В точке перегиба вторая производная равна 0 или не определена.

Физический смысл второй производной: если s(t) – функция зависимости пройденного расстояния от времени, то – это ускорение.

4. Исследование функций

При построении графиков функций сначала проводим исследование по следующему примерному плану.

1. Область определения функции, точки разрыва.

2. Наличие вспомогательных свойств: четность, нечетность, периодичность.

3. Точки пересечения с координатными осями, промежутки знакопостоянства.

4. Асимптоты.

5. Экстремумы, промежутки возрастания, убывания.

6. Выпуклость, точки перегиба.

7. Построение эскиза графика.

При необходимости для построения графика можно найти несколько дополнительных точек.

Введем или напомним необходимые определения.

Функция y = f(x) называется четной, если ее область определения симметрична относительно 0 и для каждого х из области определения f(–x) = f(x).

Функция y = f(x) называется нечетной, если ее область определения симметрична относительно 0 и для каждого х из области определения f(–x) = –f(x).

Функция y = f(x) называется периодической, если существует такое положительное число Т, называемое периодом, что вместе с любым х из области определения х – Т и х + Т также принадлежат области определения, и f(x+Т) = f(x).

Асимптотой графика функции называется прямая, к которой неограниченно приближается ветвь графика функции при неограниченном удалении этой ветви от начала координат.

Асимптоты могут быть вертикальные или наклонные, к которым можно отнести и горизонтальные. Например, график функции имеет вертикальную асимптоту х = 0 и горизонтальную y = 0.

Наличие вертикальной асимптоты х = а означает, что .

Наклонная или горизонтальная асимптота имеет уравнение y = kx + b. Параметры k и b находятся по формулам:

;

.

Если хотя бы один из этих пределов не существует, то асимптота отсутствует. При этом возможно, что придется отдельно рассматривать пределы при х → + и х → –.

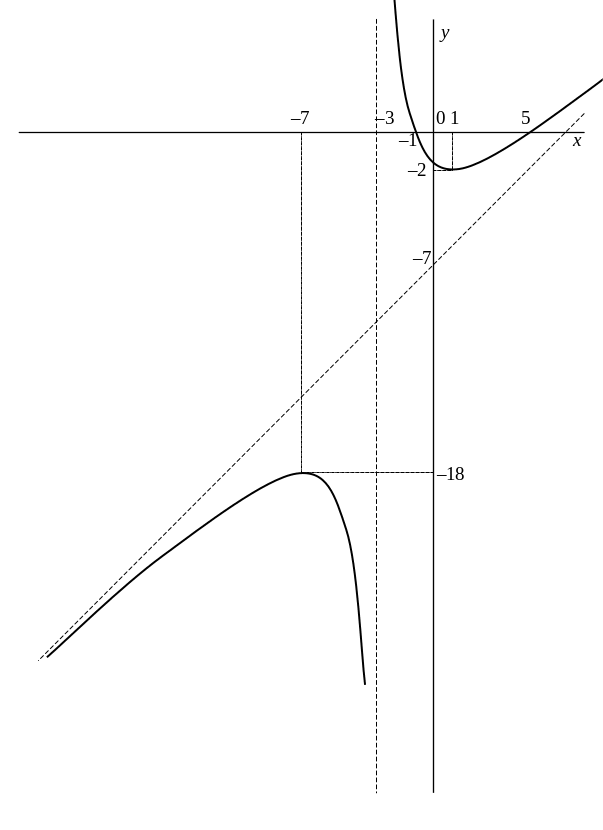
Пример 1.2.4. Провести исследование и построить эскиз графика функции .

Решение.

1. ООФ: х ≠ –3. Точка –3 есть точка разрыва.

2. . Видим, что f(–x) ≠ f(x), f(–x) ≠ –f(x), значит, функция не является ни четной, ни нечетной.

3. , значит, точка пересечения с осью ординат . Точки пересечения с осью абсцисс, то есть нули функции, находим, решая уравнение f(x) = 0. Получаем x² – 4x – 5 = 0, x₁ = –1, x₂ = 5. Определяем знаки в каждом промежутке, на которые ООФ разбивается нулями и точками разрыва.

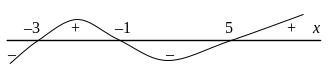
Здесь при расстановке знаков мы применили метод интервалов и правило чередования знаков. Для этого функцию представили в виде и заметили, что каждый множитель, соответствующий нулю или точке разрыва, входит в выражение в первой степени. Поэтому при переходе через каждую из этих точек знак функции меняется. Знак в самой правой области можно определить, подставив формально значение х, равное +. Тогда все скобки будут иметь знак «+».

4. Вертикальная асимптота х = –3.

Для нахождения наклонных асимптот находим последовательно:

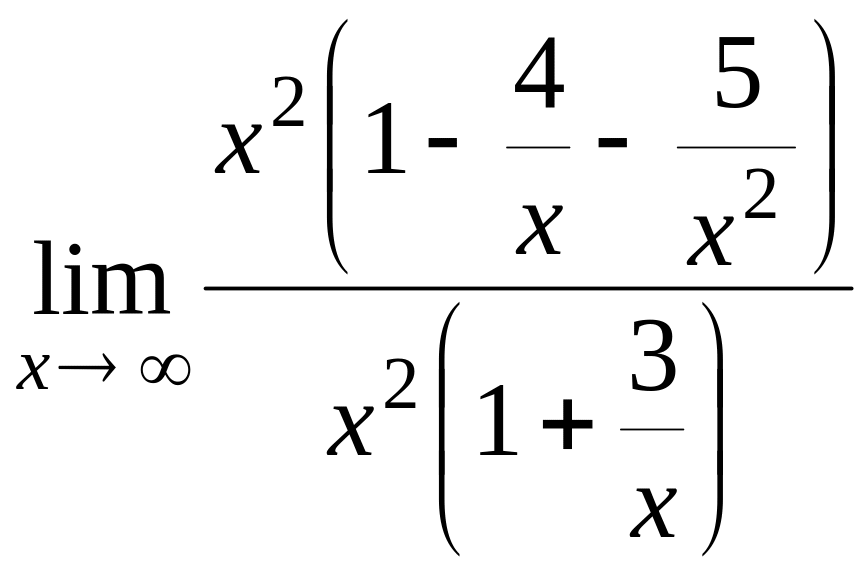= = = 1 = k;

= = = = = –7 = b.

Наклонная асимптота y = x – 7.

5. Находим производную:

= = = = = .

Нули производной –7 и 1, точка разрыва –3. Составляем таблицу:

x	(–; –7)	–7	(–7; –3)	(–3; 1)	1	(1; +)
	+	0	–	–	0	+
f(x)		–18			–2
экстремум		max			min

6. Находим вторую производную:

= = = = = = = .

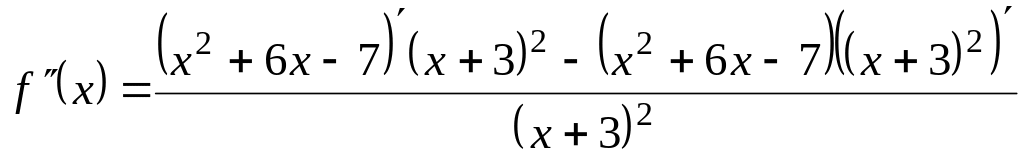Замечаем, что ≠ 0, и точка, где не определена, не принадлежит ООФ. Значит, точек перегиба нет. Определяем промежутки выпуклости с помощью таблицы:

x	(–; –3)	(–3; +)
	+	–
f(x)

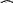
7. Рисуем график, используя всю полученную информацию:

У п р а ж н е н и я

1.2.1. Найдите производные следующих функций:

1. 2x³ – 5x² + x – 4;

2. sin 2x – ln x;

3. (x² + 3x – 1) cos x;

4. e^{2x – 1}tg x;

5. (3x³ + 5x – 2) ln x;

6. ;

7. ;

8. ;

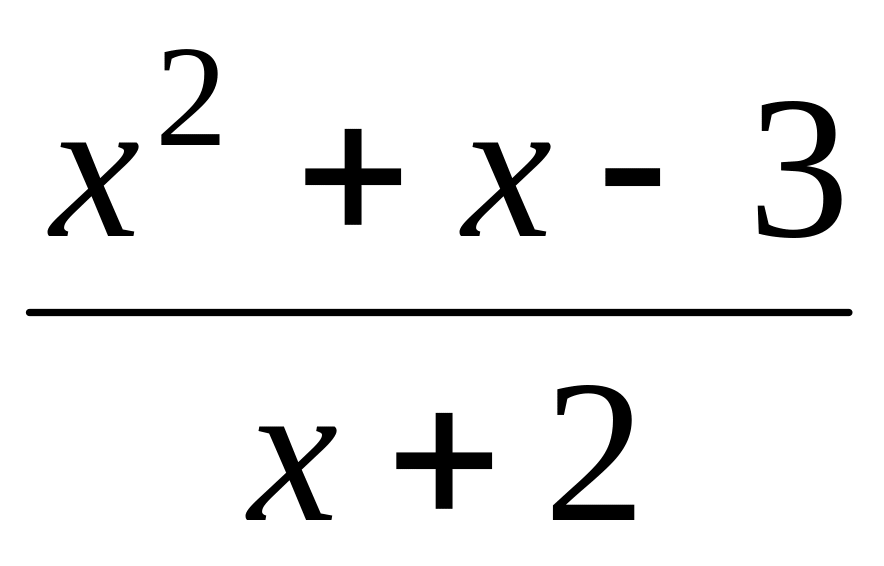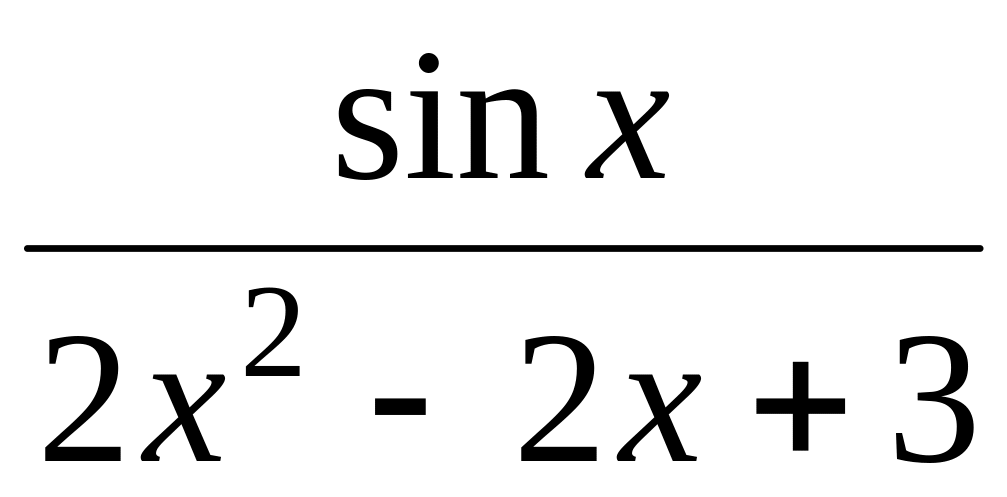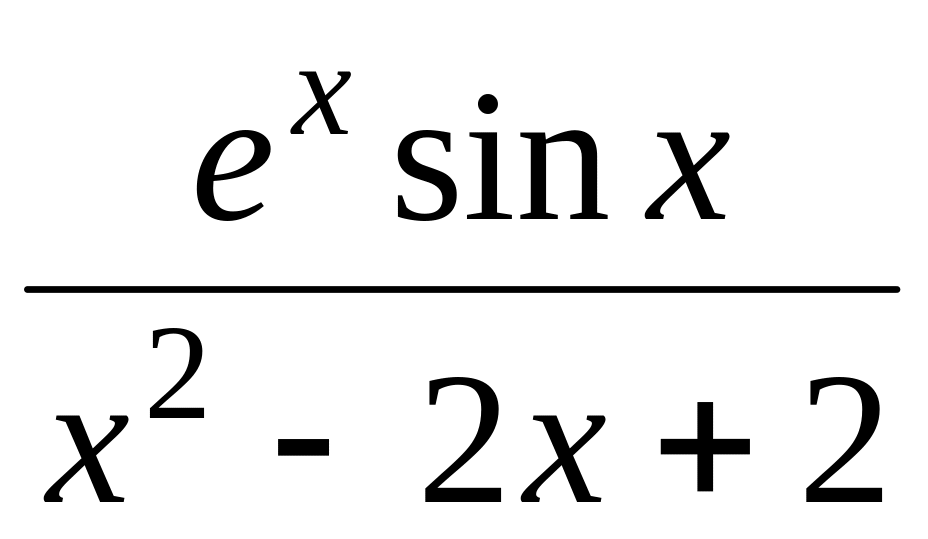9. sin (x² + x – 4);

10. ;

11. ;

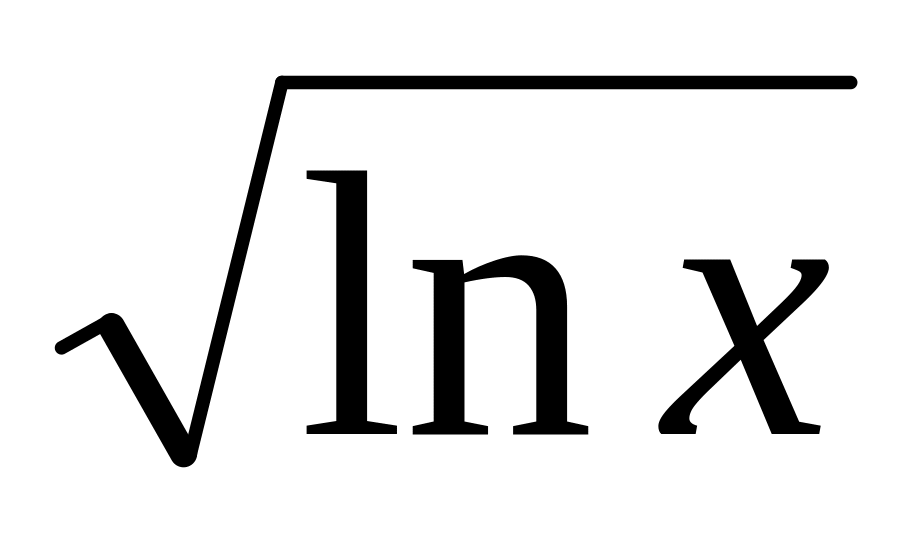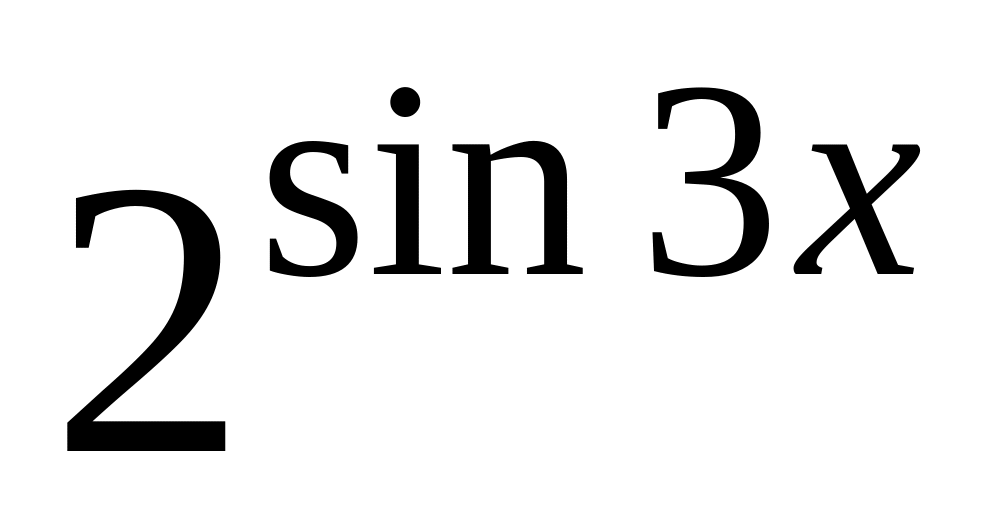12. cos² 2x;

13. arcsin (x² + 3x +1);

14. .

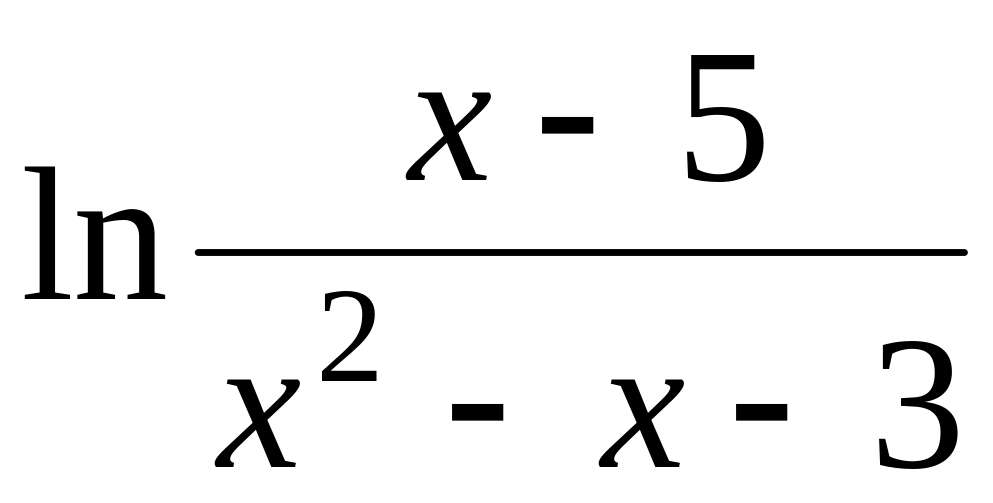15. e^{x sin x};

16. .

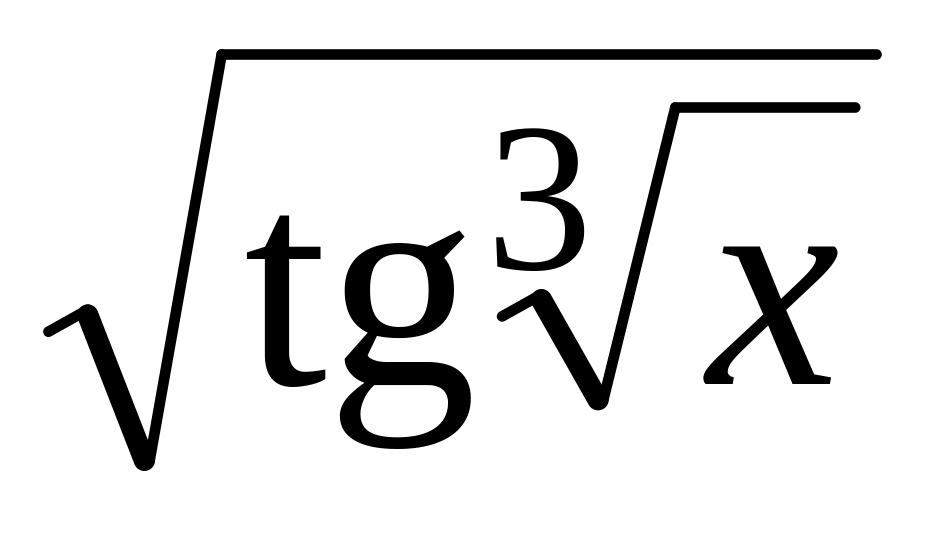1.2.2. Найдите пределы по правилу Лопиталя:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

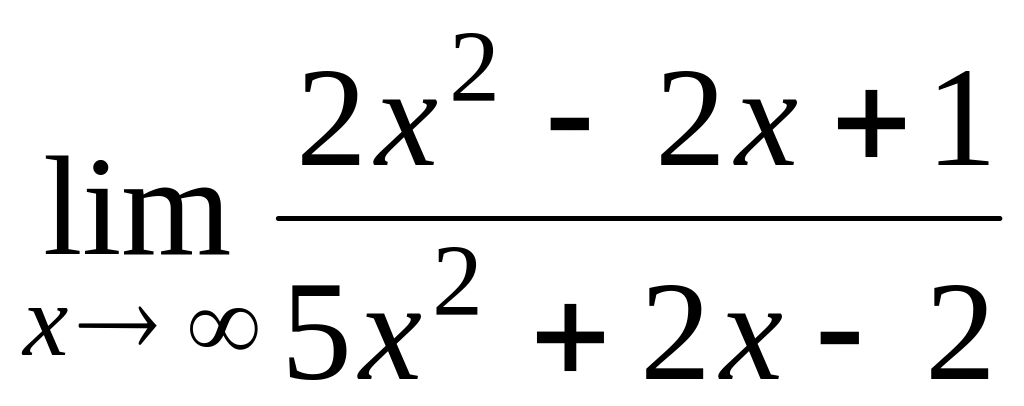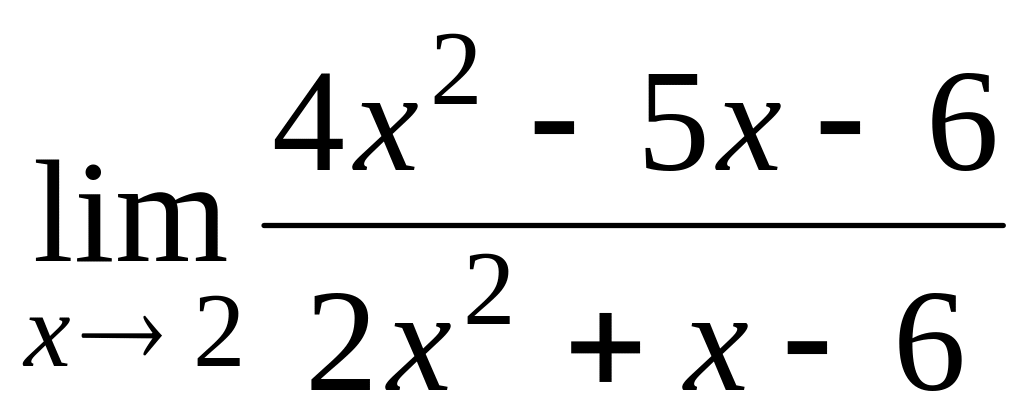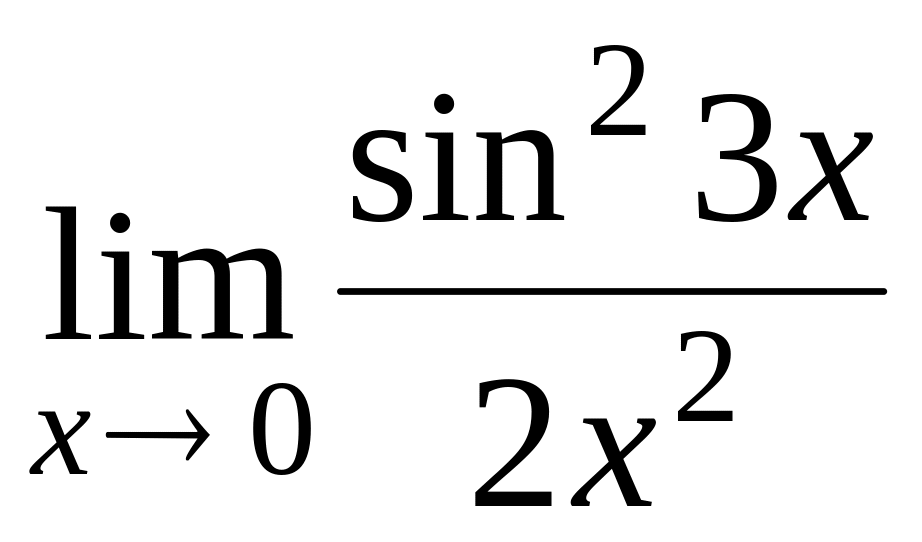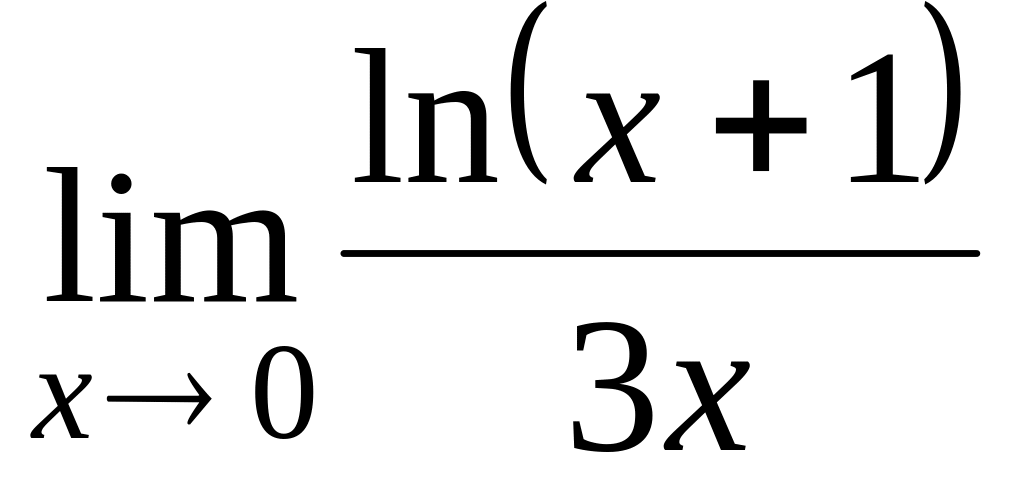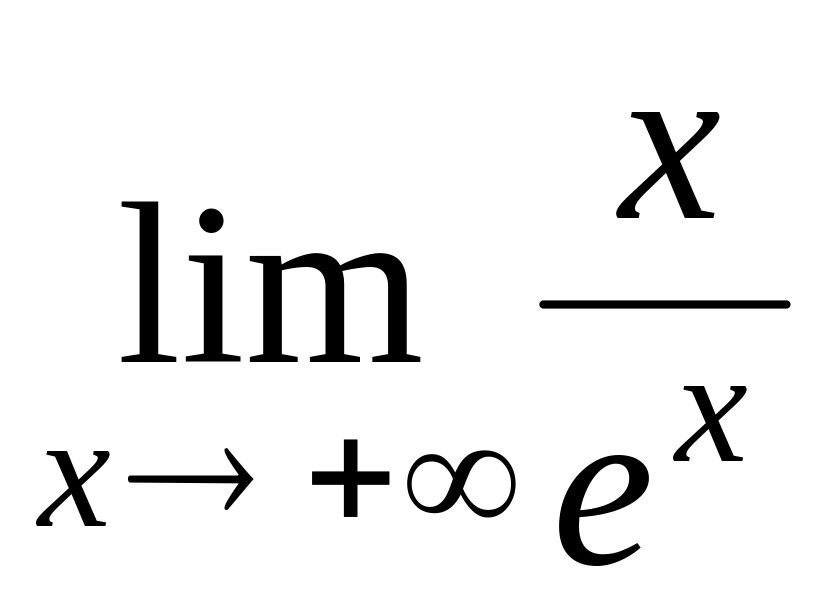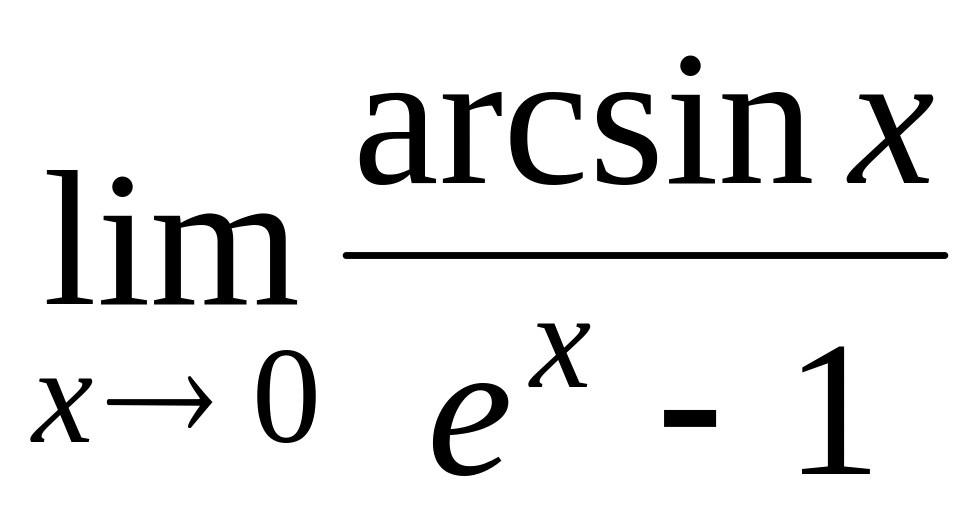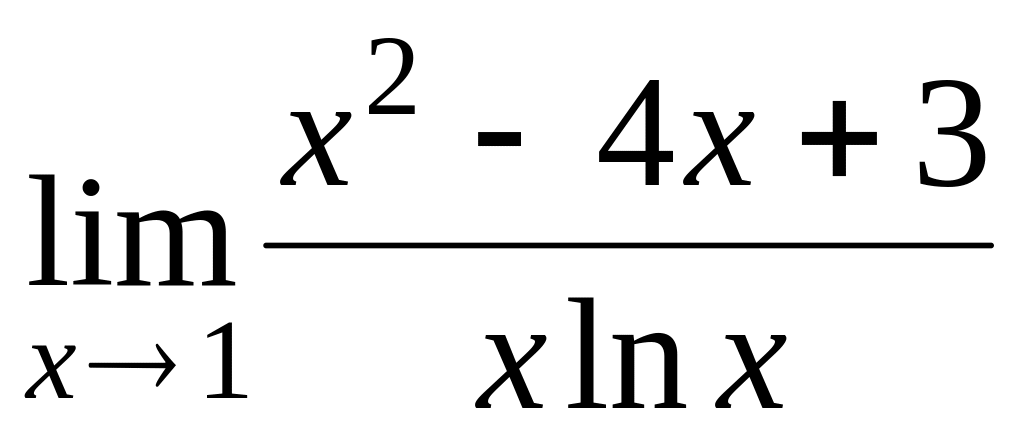1.2.3. Найдите асимптоты следующих функций:

1. ;

2. ;

3. .

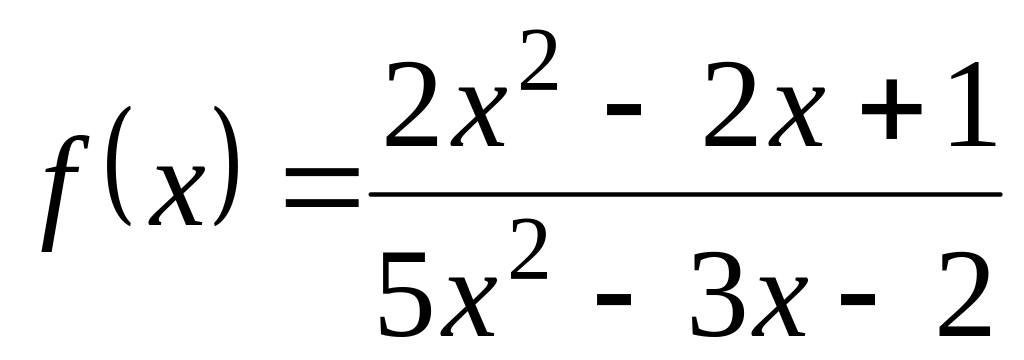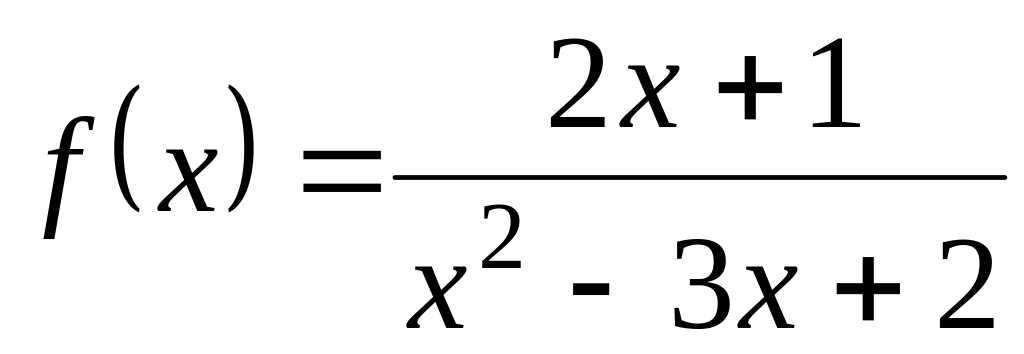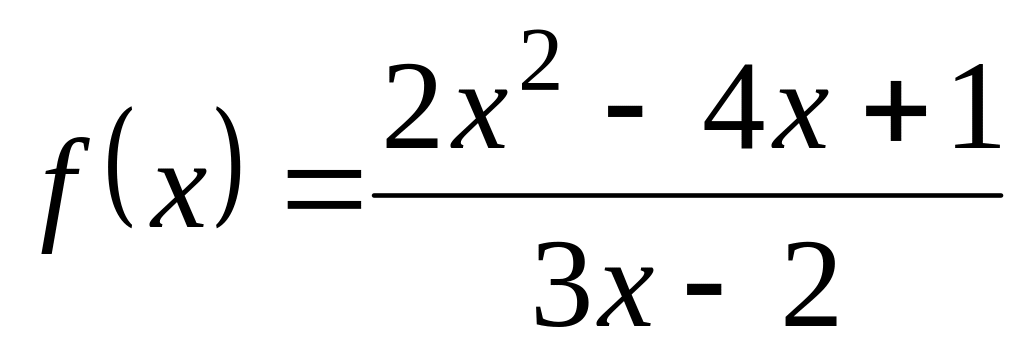1.2.3. Исследуйте функцию и постройте эскиз графика:

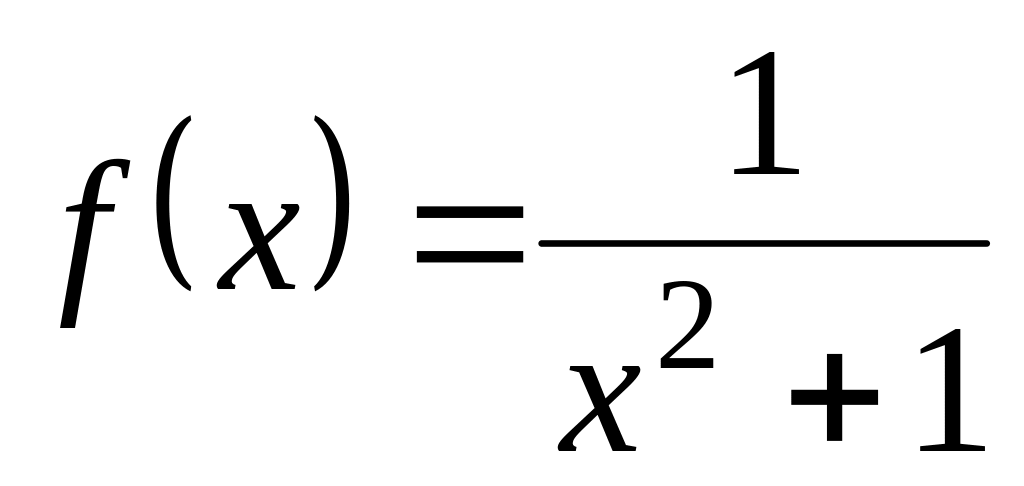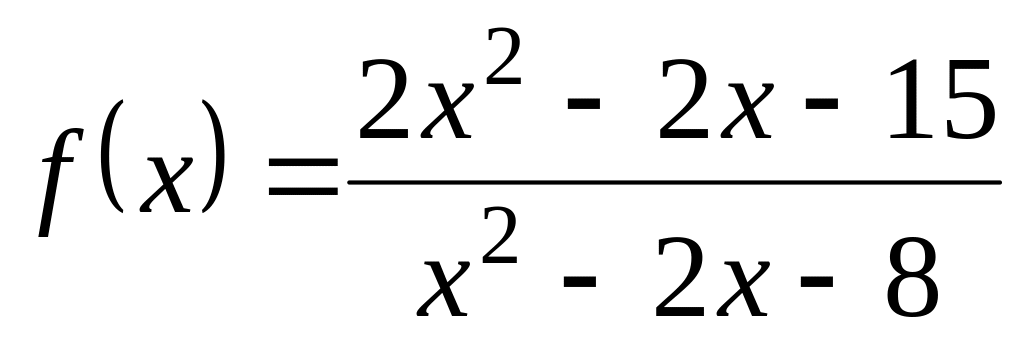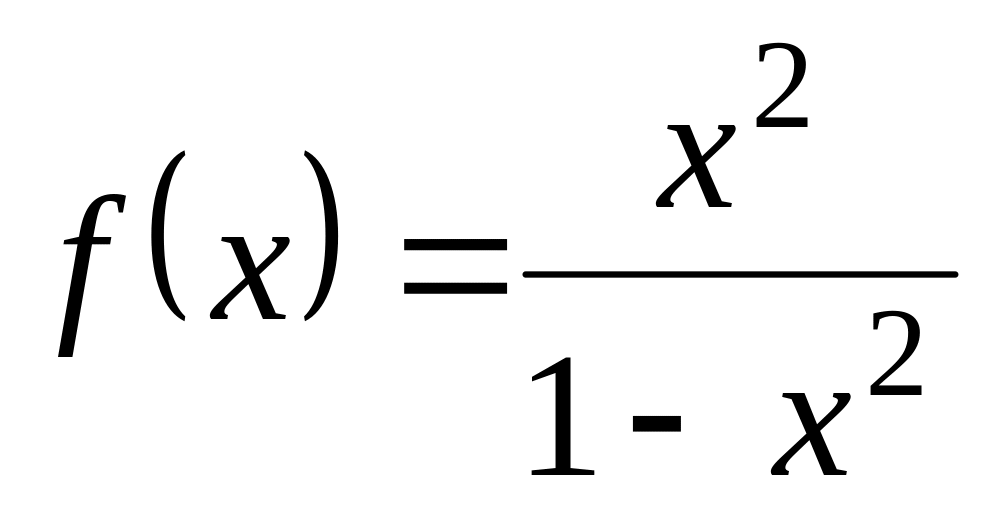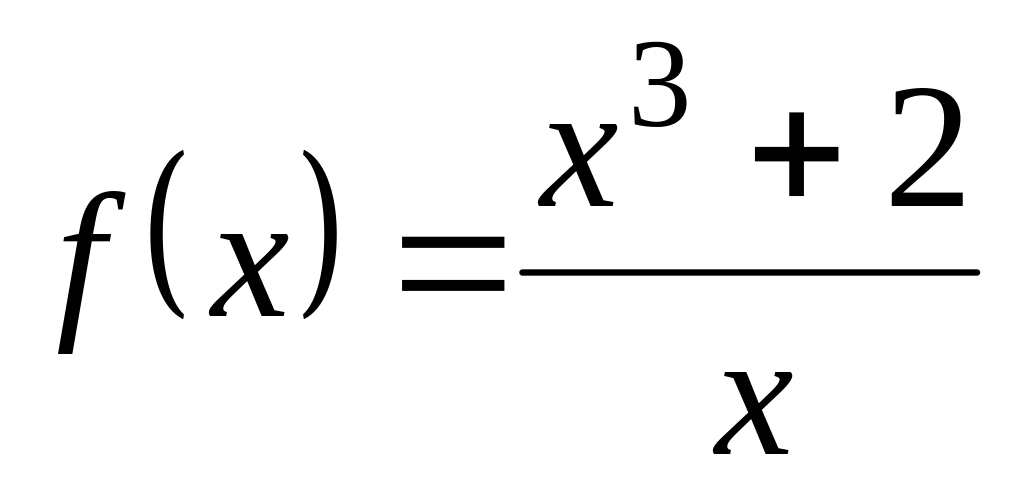1. ;

2. ;

3. ;

4. ;

5. .