3.Элементы интегрального исчисления
1. Неопределенный интеграл
Функция F(x) называется первообразной для функции f(x), если f(x) =
.
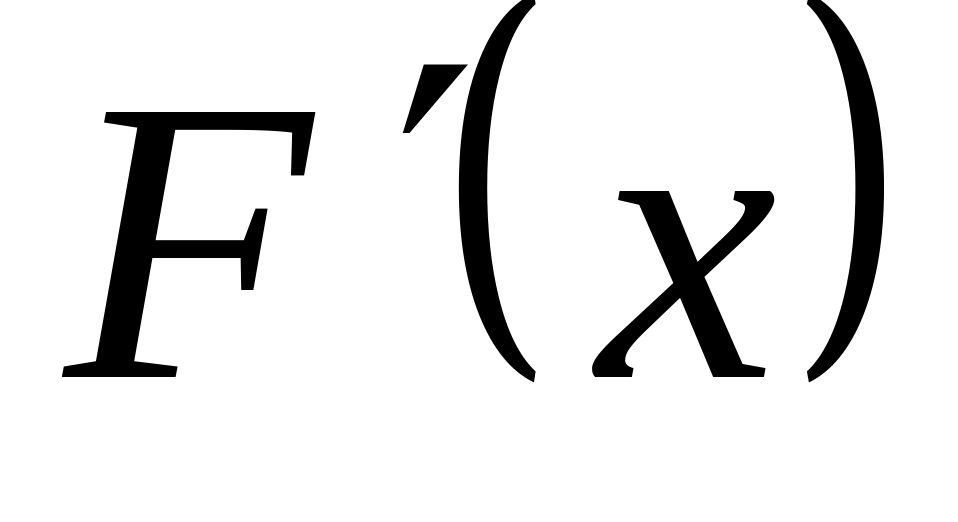Заметим, что если F(x)
является первообразной для функции
f(x),
то первообразными будут также все
функции вида F(x)
+ С, где С – произвольная
константа. Множество всех таких функций
называется неопределенным интегралом
от функции f(x)
и обозначается
.
Выражение dx под знаком интеграла есть дифференциал, его роль в этом выражении будет выяснена позже.
Используя таблицу производных, можно получить таблицу основных интегралов:
,
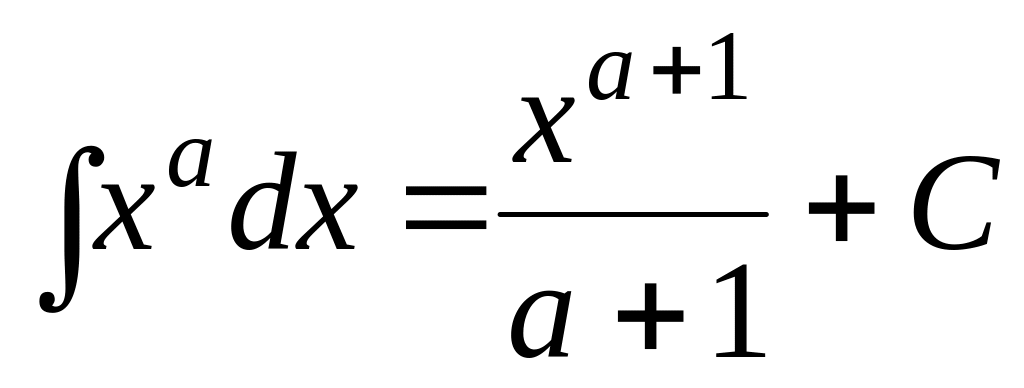где а≠ –1;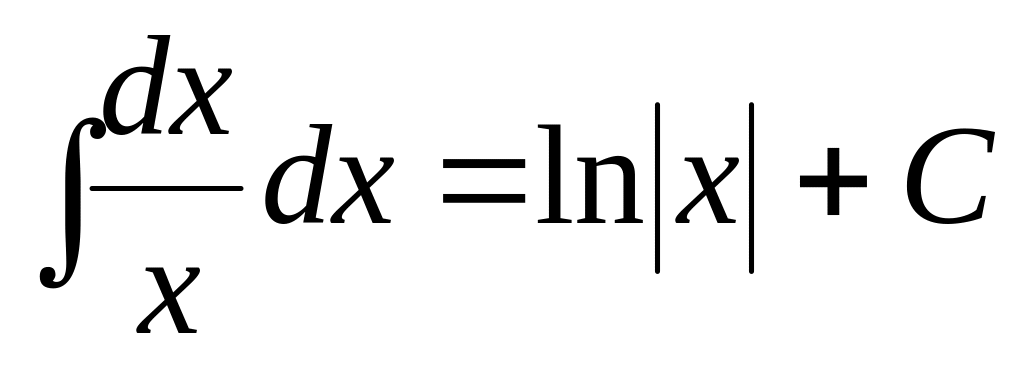
;
,
;
;
;
;
;
;
.
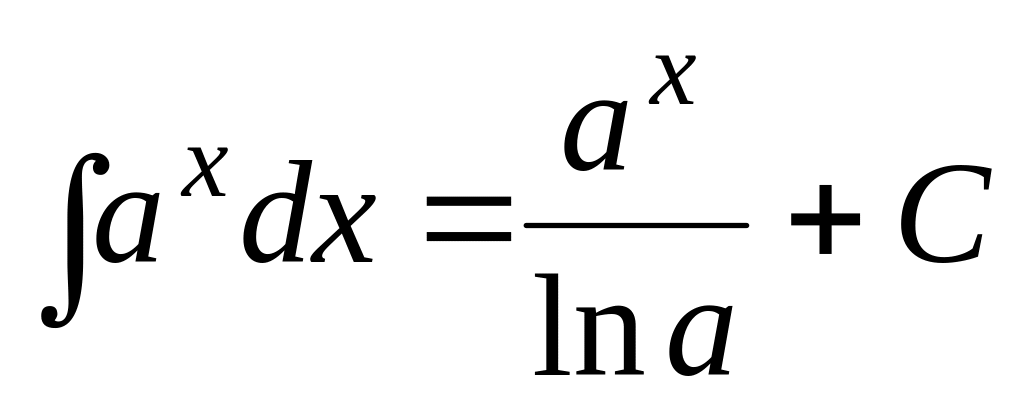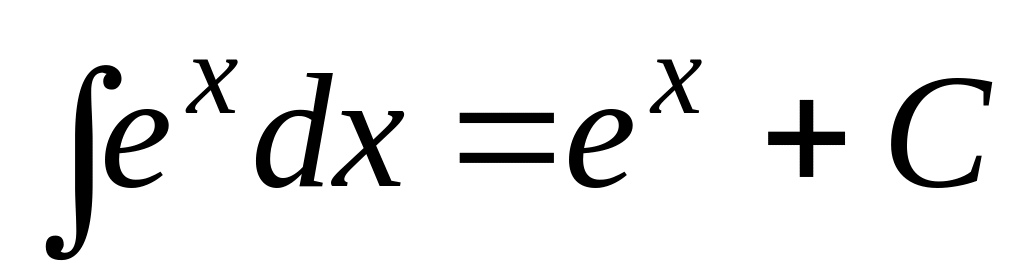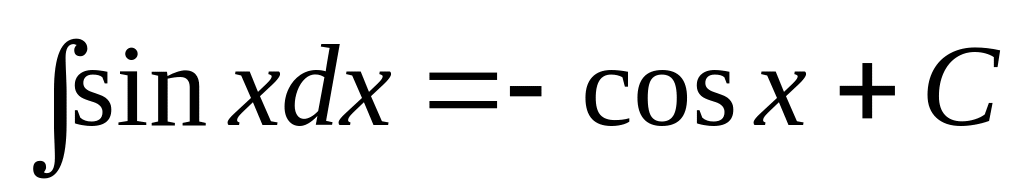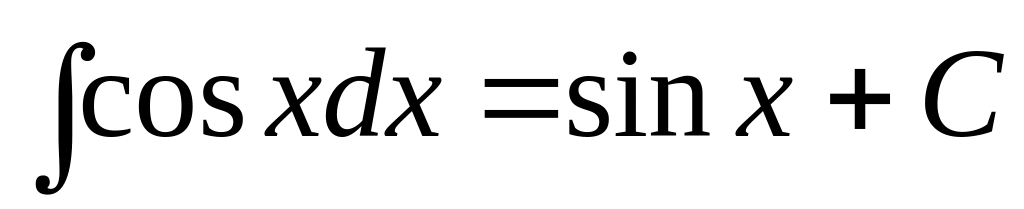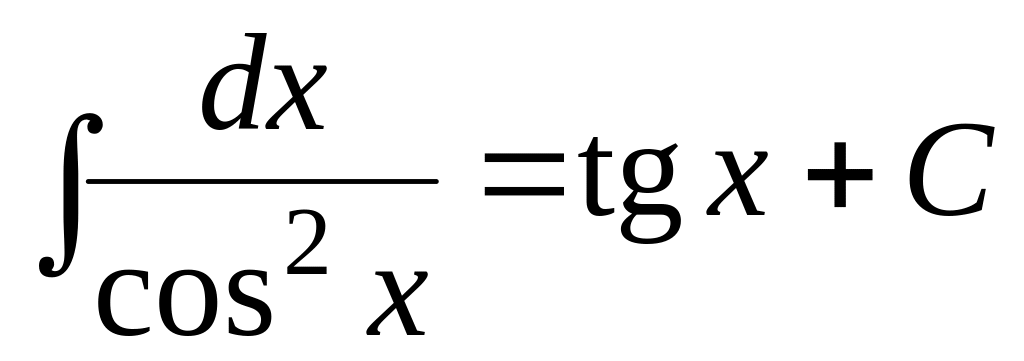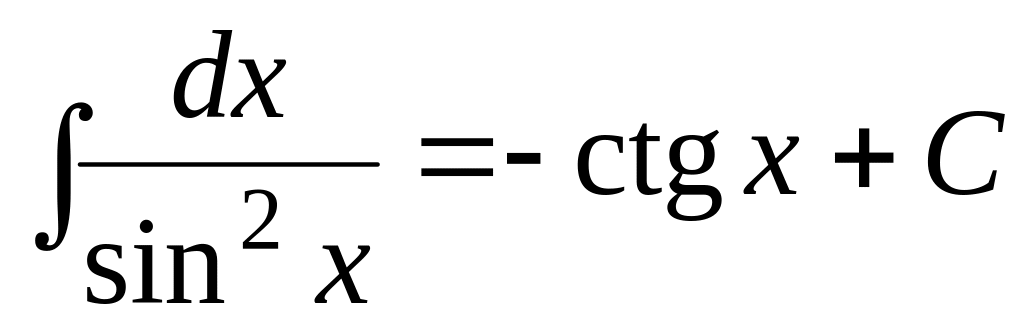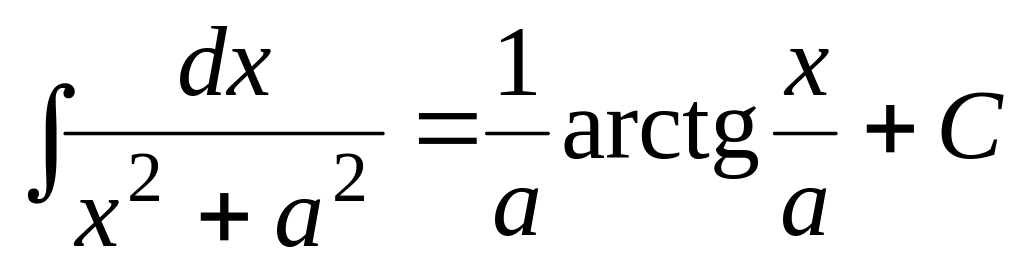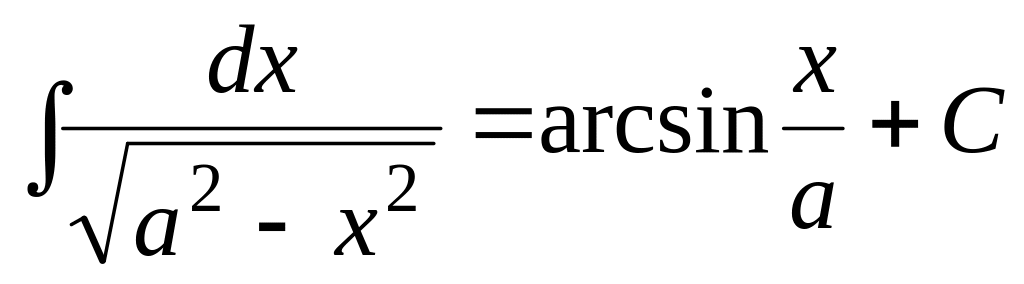Вычисление других интегралов основано на их свойствах:
;
,
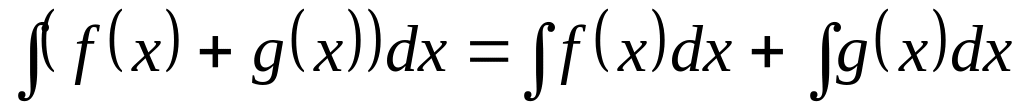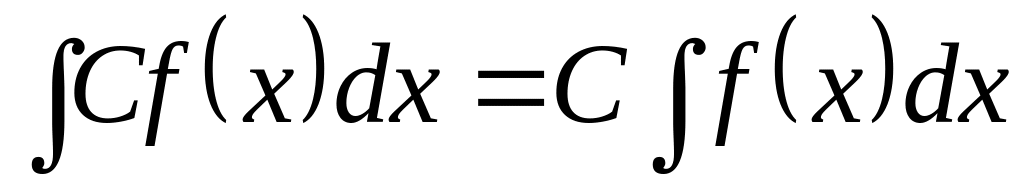где С – константа.
Производную можно найти от любой элементарной функции. Интеграл же существует для любой непрерывной или кусочно непрерывной функции, но аналитическое выражение для него можно получить далеко не всегда. Рассмотрим основные приемы интегрирования.
А) Сведение к табличным интегралам.
Пример
1.3.1.
=
= =
.
Б) Замена переменной.
Если
не приводится к табличному непосредственно,
можно произвести замену переменной
вида x = (t)
с целью преобразовать подынтегральную
функцию к более удобному для интегрирования
виду. При этом будем иметь
,
.
Необходимые формулы обычно пишут прямо
в строке, отделив от основных преобразований
косыми чертами. Получив результат с
новой переменной, необходимо вернуться
к старой.
Пример 1.3.2. Вычислить
интеграл
.
Решение.
=
=
=
=
–cos t
+ C =
.
Часто замену переменной
производят с помощью соотношения (x)
= t, если в подынтегральной
функции явно выделяется выражение
(x).
В этом случае dt =
,
и такая замена может быть удачной, если
также явно присутствует.
Пример 1.3.3. Вычислить
интеграл
.
Решение.
=
=
=
=
=
=
=
.
Выкладки в преобразованиях можно сократить, если не вводить новую переменную заменой (x) = t, а производить преобразования прямо с выражением (x). В частности, его можно ввести под знак дифференциала.
Пример 1.3.4.
=
=
.
С помощью замены переменной можно вывести следующее правило интегрирования:
III.
Если
,
то
.
В) Интегрирование по частям
Этот метод основан на формуле
.
Пример 1.3.5.
=
=
=
.
Интегрирование по частям оказывается эффективным, например, если подынтегральная функция имеет вид exf(x), sin xf(x), cos xf(x), где f(x) – многочлен. В этих случаях в зависимости от степени многочлена интегрирование по частям производим несколько раз. Каждый раз под знак дифференциала отправляем тригонометрическую или показательную функцию. В результате после применения формулы она поменяется местами с многочленом, и после дифференцирования степень многочлена понижается.
Если же подынтегральная функция имеет вид ln x f(x), где f(x) – многочлен, то под знак дифференциала отправляем многочлен. В результате его степень повысится, но затем он меняется местами с логарифмом, и в результате дифференцирования логарифмическая функция превращается в степенную.
Пример 1.3.6.
=
=
=
=
=
=
=
=
.