4.9 Геометрические характеристики сечений при изгибе

Следует помнить, что для стандартных профилей (уголки, двутавры, швеллеры и т.д.) все геометрические характеристики имеются в справочной литературе. Определим геометрические характеристики других сечений:

1) Прямоугольное сечение (рис.4.16).

у dА

dy

h у

x

А

b

Рисунок 4.16 – Прямоугольное сечение

На расстоянии У от нейтральной оси Х выделим элемент dA, ширина элемента b, высота dу.

I_x = _Ау²dA; dA = b = dy;

I_x = b _Ау²dy; I_x = -_h/2^h/2y²dA = bh³/12; (4.17)

W_x = I_x/h2 = bh²/6. (4.18)

Аналогично

I_y = hb³/12. (4.19)

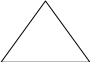
2 ) Треугольное сечение (рис 4.17): у

у

х₁

dA b_x dy

h

 x_c

ц.т.

х₂

b

Рисунок 4.17 – Треугольное сечение

b_x = b/hy; dA = b/hydy; I_x1 = ₀^h у²b/h ydy;

I_x1 = bh³/4. (4.20)

Момент инерции относительно центральной оси, параллельной основанию.

Для вывода этой формулы воспользуемся формулой для параллельных осей:

I_xc = Ix₁ – (2h/3)²A = bh³/4 – 4h²/9bh/2;

I_xc = bh³/36. (4.21)

Момент инерции относительно оси, проходящей через основание (рис.4.18):

у

у

dA b_x dy

h

x_c

А

х₂

b

Рисунок 4.18 – Треугольное сечение

I_x2 = _A y²dA = _Ay²b_xdy; b_x/b = h – y/h; b_y = b(h - y)/h;

I_x2 = ₀^hb(1 – y/h)y²dy = bh³/3 – bh³/4; I_x2 = bh³/12. (4.22)

Аналогично получим

I_y = hb³/48. (4.23)

Очевидно, что центральная ось Х не является осью симметрии, следовательно, моменты сопротивления для крайних волокон будут иметь различные значения (рис. 4.19).

у

С _c

--

y₂^max + 

h

x_c

А y₁^max –

А

b _A

Рисунок 4.19 – К определению момента сопротивления и напряжений

Момент сопротивления для точки С:

W_xc = I_xc /(2/3)h = bh³3 / 362h = bh² / 24. (4.24)

Для точки А:

W_xА = bh³ / 36 (1/3) h = bh² / 12. (4.25)

Следовательно,

_с = M / W_с = (М / bh²) 24;

_А = M / W_А = (М / bh²)  12.

3) Круглое сечение (рис.4.20):

I_x = I_y = D⁴ / 64; (4.26)

W_x = W_y = 0,1D⁴. (4.27)

y

x

D

Рисунок 4.20 – Круглое сечение

4) Полое сечение (рис.4.21):

I_x^нетто = bh³ / 12 – b₁h₁³ / 12; W_x = (I_x^нетто / h)2;

I_y^нетто = hb³ / 12 – h₁b₁³ / 12; W_y = (I_y^нетто / b)2.

y

h/2

h h₁

x

h/2

b₁

b

Рисунок 4.21 – Полое сечение