4.5 Дифференциальные зависимости при изгибе

Рассмотрим схему балки, нагруженную произвольными силами (рис.4.6).

Q q

А 1 2 Р В

М М+dМ

С

Q+dQ

dz y

М 1 2 dz

а) б)

Рисунок 4.6 – К определению дифференциальных зависимостей: а) схема нагружения;

б) внутренние силовые факторы

Составим два уравнения равновесия. Сумма проекций на ось y:

 Р_y = 0; Q + qdz – Q – dQ = 0;

q = dQ / dz . (4.3)

Сумма моментов всех сил относительно точки С равна нулю.

 М_с = 0; – М + q dz² / 2 +М+dМ – Q dz + dQ dz = 0.

Пренебрегая бесконечно малыми величинами qdz²/2 и dQdz, получим:

Q = dМ / dz . (4.4)

C учетом (4.4) имеем

q = d²М / dz² . (4.5)

Выражения (4.3), (4.4), (4.5) используются для контроля построения эпюр поперечных сил и изгибающих моментов.

4.6 Контроль построения эпюр поперечных сил и изгибающих моментов

Контроль построения эпюр основан на выражениях (4.3) – (4.5). Согласно формулам приходим к следующим заключениям:

1) В тех местах, где действует сосредоточенная сила, на эпюре поперечных сил имеется скачок на величину этой силы, а на эпюре изгибающих моментов – излом (рис.4.7).

А Р В

а

L

Q

А + + В Р

– –

М_max=Aa Q

Рисунок 4.7 – Схема для контроля построения эпюр

М

а В

A

Q

+

А – –

• 

М

М + +

– –

Aa

Рисунок 4.8 – Схема для контроля построения эпюр

2) В тех местах, где действует момент М, на эпюре моментов будет скачок на величину это-го момента, а на эпюре поперечных сил это не отражается (рис.4.8).

3) В тех местах, где действует постоянная распределенная нагрузка, эпюра изгибающих моментов ограничена квадратной параболой, а эпюра поперечных сил – наклонной линией (рис. 4.9).

A = ql / 2 1 q B = ql / 2

z₁

1

l

ql / 2 Q

+

–

M M_max =ql² / 8

+

z^* = l / 2

Рисунок 4. 9 – Схема для контроля построения эпюр

4) В тех местах, где эпюра поперечных сил плавно (без скачков) меняет знак с плюса на минус или наоборот, на эпюре моментов будет экстремум (рис.4.9). Необязательно, что это наибольший момент на рассматриваемом пролете. В некоторых задачах это наименьший момент.

Однако исследовать сечение при z^* обязательно и необходимо. Обратимся к задаче на рисунке (4.9).

Опорные реакции:

А = B = ql / 2.

Поперечная сила в сечении 1-1:

Q_{1-1 =} A - qz₁; 0 = < z₁ = < l;

z₁ = 0; Q = ql / 2; z₁ = l; Q = ql / 2 - ql; Q = -ql / 2.

Определим z^*:

0 = ql / 2 - qz^*; z^* = l/2.

Изгибающие моменты:

M_1-1 = Az₁ - qz₁² / 2; z₁ = 0; M = 0.

z₁ = z^* = l / 2; M = ql² / 4 – q(l/2)² / 2 = ql² / 8.

5) В том случае, когда равномерно распределенная нагрузка направлена вниз, т.е.

d²M/dz²<0,

выпуклость кривой, ограничивающей эпюру изгибающего момента, направлена вверх – навстречу направлению действия распределенной нагрузки, если эпюра М строится на сжатом волокне и обращена вниз – по направлению действия нагрузки q, если эпюра М строится на растянутом волокне. При обратном направлении нагрузки (вверх) выпуклость кривой тоже имеет обратное направление.

6) На тех участках балки, где эпюра Q положительна, изгибающий момент с увеличением координаты z увеличивается, так как

dM / dz = Q > 0,

и, наоборот, там, где Q < 0, изгибающий момент уменьшается. На участках, где q = 0, изгибающий момент имеет постоянное значение.

Пример 4.1. Деревянная консольная балка, жестко защемленная одним концом, нагружена сосредоточенной силой P, моментом M и распределенной нагрузкой q(рис 4.10).

Определить внутренние усилия по участкам балки, построить эпюры Q и M, определить наибольшие нормальные и касательные напряжения и сравнить их с допускаемыми. Допускаемые напряжения для дерева (сосна) на растяжение и сжатие при изгибе [] = 12 МПа и на сдвиг [] = 8 МПа.

Исходные данные:

a = 1,5 м, b = 1 м, с = 0,5 м,

P = 0,5 Кн, q = 0,4 кН/м, m = 0,2 кг

m

а ) q 3 2 1 z₁

180мм

3 2 z₂ 1 Р

z₃ 120мм

а в с

0,5

б )

+ z₃^*

–

0,5 0,5

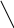0,762

0,75

0,55 0,25

0,45

в )

+ +

Рисунок 4.10 – Схема к расчету: а) заданная нагрузка; б) эпюра поперечных сил; в) эпюра изгибающих моментов

Определяем внутренние усилия Q и М в поперечных сечениях балки методом сечения. Для этого условно рассекаем балку в произвольном месте каждого участка плоскостями 1-1, 2-2, 3-3. Из условия равновесия отсеченной части балки определяем поперечную силу Q и изгибающий момент М на каждом участке.

Сечение 1-1:

Q_z1 = – Р, М _z1 = Р z _, 0 < z < c .

Сечение 2-2:

Q_z2 = – Р + q(z₂ – c), M_z2 = P z₂ – q(z₂ – c)²/2, c <z₂ < b + c