2.5. Выпуклость и вогнутость кривой. Точки перегиба. Динамика монотонного изменения функции
Кривая
называется выпуклой
(
вогнутой
) в точке
,
если в некоторой окрестности этой
точки кривая расположена ниже ( выше
) своей касательной . Если в точке
то кривая вогнута. Если
то кривая выпукла.
Т
очка,
в которой выпуклая (вогнутая) становится
вогнутой (выпуклой), то есть кривая
переходит с одной стороны касательной
на другую называется точкой
перегиба. Необходимое
условие перегиба в точке
– нулевая или
несуществующая производная второго
порядка.
Необходимое условие не является, однако,
достаточным, то есть обратное не всегда
верно Достаточное
условие перегиба – смена знака второй
производной
в окрестности точки перегиба.
Здесь, в точке перегиба, меняется характер
монотонности
Заметим, что если
или не существует, но
не является экстремальной точкой, то
это - точка перегиба. То есть, критическая
точка не является экстремальной точкой,
она представляет собой точку перегиба.
В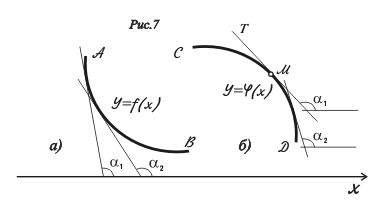
ыпуклость
или вогнутость графика связана с
характерными особенностями функции.
На интервалах монотонности скорость
изменения функции может возрастать или
уменьшаться. При этом график функции
оказывается выпуклым или вогнутым
(рис 6 и 7)
На рис.6
кривая АВ
лежит ниже касательной МТ
– это выпуклая кривая. СD
– вогнутая кривая. Она вся располагается
выше любой касательной.
На
рис. 6 кривые АВ
и СD
характеризуют возрастающие функции.
Но характер роста этих функций различный.
Скорость роста
уменьшается,
и первая производная представляет собой
убывающую функцию, поэтому здесь вторая
производная
В случае кривой СD
скорость роста функции
увеличивается. Здесь
,
является возрастающей функцией и
Аналогичная
ситуация характерна и для убывающих
функций. Функция может замедлять свой
спад, тогда
будет
отрицательной возрастающей функцией
и ускорение, с которым изменяется
функция, будет положительным (
),
как производная возрастающей функции
(на рис. 7а
–
кривая АВ,
функция
).
Скорость
спада убывающей функции может нарастать,
как у функции
на
рис. 7б,
кривая
СD.
Здесь
.
Поэтому неположительная
является убывающей функцией
.
Ускорение, с которым изменяется функция,
то есть
также будет отрицательным, как производная
убывающей функции. Действительно, чтобы
скорость увеличивалась, знаки ускорения
и скорости должны совпадать. Скорость
спада увеличивается, если ускорение
отрицательно (кривая
СD
на рис.
7б), скорость спада
уменьшается, если ускорение
положительно
(кривая
АВ, рис. 7а)
Таким образом, выпуклость или вогнутость графика функции отражает особенности ее роста (или спада), то есть характеризует динамику функции.
На
интервалах выпуклости темпы роста
функции уменьшаются. Здесь
,
а ускорение отрицательно (
и возрастание функции замедляется.
Темпы спада функции на интервалах
выпуклости, напротив, увеличиваются.
Здесь и скорость и ускорение отрицательны.
При этом
и ускорение положительно (
),
и функция возрастает все быстрее.
Темпы спада убывающей функции на
интервалах вогнутости уменьшаются.
Функция убывает все медленнее, так
как при отрицательной скорости изменения
функции наблюдается положительное
ускорение:
.
Схема исследования функции на выпуклость, вогнутость и точки перегиба. Выявление особенностей монотонного изменения функции.
1. Найти
вторую производную функции
2. Найти
точки, в которых вторая производная
или не существует.
3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и вогнутости и наличии точек перегиба.
4. Найти значения функции в точках перегиба.
5. Сделать
заключение об особенностях поведения
функции на интервалах монотонности,
анализируя знаки
и
Пример1.
Найти интервалы выпуклости и вогнутости,
и точки перегиба графика функции
Установить особенности изменения
функции на интервалах монотонности
(см. рис. 5).
► Поскольку интервалы выпуклости и вогнутости графика функции – это интервалы знакопостоянства второй производной, а точка перегиба – это точка, в которой вторая производная функции равна нулю или не существует, необходимо найти и проанализировать вторую производную функции
,
и
;
;
при
и
Нетрудно
заметить, что
на интервалах
и
,
а на интервале
.
Поскольку в окрестности
и
наблюдается смена знака второй
производной, точки
и
есть точки перегиба (рис.
5).
.
График
функции оказывается вогнутым на множестве
и
и
выпуклым на
При этом скорость спада исследуемой
функции на интервале
постепенно уменьшается, до точки
,
здесь
.
Это точка минимума функции, скорость
ее изменения в этой точке равна нулю,
.
Затем начинается интервал монотонного
возрастания функции
,
причем на интервале
,
где график выпуклый и
скорость роста замедляется, а на остальной
части интервала монотонного возрастания
скорость роста функции постоянно
увеличивается, везде
◄
2.6. Асимптоты графика функции. При изучении функции наряду с характерными точками (критическими, экстремальными, точками перегиба) рассматриваются также характерные линии. Важнейшие из них – асимптоты.
Асимптотой функции называется прямая, к которой график функции постоянно приближается, стремясь слиться с ней в бесконечности).
График функции имеет асимптоты в следующих случаях.
1)
.
Это значит, что прямая
есть асимптота кривой
Например,
кривая
имеет асимптоту
.
2)
Если в правой части уравнения кривой
можно выделить линейную часть
так, что оставшаяся часть
когда
то
прямая
есть асимптота кривой. Примеры: а)
кривая
имеет асимптоту
(и асимптоту
);
б) кривая
имеет, кроме асимптоты
,
асимптоту
3) Если
существуют конечные пределы
и
то прямая
есть асимптота графика
.
При исследовании функции и построении ее графика рекомендуется работать в соответствии со следующей схемой.