2.7. Схема исследования функции и построения ее графика

1. Найти область определения функции.

2. Найти точки пересечения с осями координат и в дальнейшем, возможно, некоторые дополнительные точки, уточняющие график.

3. Исследовать функцию на четность – нечетность, периодичность.

4. Исследовать поведение функции в окрестности точек разрыва. Найти вертикальные асимптоты.

5. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.

6. Найти экстремумы и интервалы монотонности функции.

7. Найти интервалы выпуклости и вогнутости функции и точки перегиба.

Заметим, что исследование функции проводится одновременно с построением ее графика.

Пример1. исследовать функцию и построить ее график. .

► 1. Заданная функция определена на всем действительном множестве, кроме То есть область определения функции: x R\ ;

2. График функции имеет точки пересечения с осями координат:

а) с осью ОУ, так как здесь то . Имеем точку .

б) с осью ОХ, здесь , поэтому , имеем .

3. Заданная функция есть функция общего вида, так как и . Функция не является периодической, так как это не тригонометрическая функция.

4. Точка разрыва функции: ; Исследуем поведение функции в окрестности точки разрыва. .

П оскольку и , – вертикальная асимптота графика функции ( рис. 8 )

5. Для выявления наклонных асимптот и исследования функции на концах области определения выделим из выражения, задающего функцию, целую часть. Получим (а). Заметим, что при превращается в бесконечно малую величину. . Это означает, что исследуемая функция на концах области определения бесконечно мало отличается от своей линейной составляющей То есть наклонная асимптота функции, к которой график функции приближается сверху при и снизу при ( рис. 8 )

6. Найдем интервалы монотонного изменения функции и ее экстремальные точки. Здесь очень удобно использовать задание функции в виде (а). . не существует при но ОДЗ. если или При этом при при Таким образом, интервалы монотонного изменения функции найдены. Функция возрастает на и на убывает на и Поскольку, проходя через точки и первая производная меняет знак, а функция – характер монотонности, то и – точки экстремумов функции. – точка max , – точка min. .

7. Выясним особенности монотонного изменения функции. То есть уточним характер монотонности, ее динамику. Для этого нужно узнать, как ведет себя скорость изменения функции, то есть первая производная. Нужную информацию дает вторая производная, На области определения функции , при то есть при Это означает, что на множестве , где функция возрастает, скорость ее роста будет постепенно уменьшаться

На промежутке функция убывает, скорость ее спада здесь будет постоянно увеличиваться, так как ускорение также отрицательно, . График функции на будет выпуклым, поскольку .

при то есть при При ускорение положительно ( ). Следовательно, на участке спада убывание функции постепенно замедляется и спад прекращается при Здесь скорость изменения функции равна нулю, Дальше, на , начинается рост функции. Здесь и то есть скорость роста функции постоянно увеличивается. График функции здесь, на , вогнутый.

И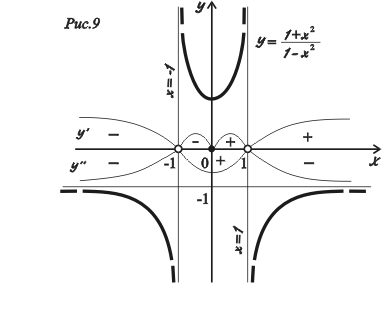 так, результаты исследования укла­дываются в единую непротиворечивую схему, позволяя пос­троить график функции ( рис. 8 ). ◄

Пример2. Исследовать функцию и построить ее график.

► 1. Область определения , то есть

, следовательно, – точка пересечения графика функции с осью ординат. Уравнение не имеет решений на действительном множестве, значит, точки пересечения графика функции с осью ОХ отсутствуют.

2. Функция четная, так как Следовательно, график функции симметричен относительно оси ординат.

3. Функция неопределена при Исследуем поведение функции в окрестности То есть рассмотрим соответствующие предельные значения .

и . Так как пределы функции слева при , и справа, при , бесконечны, то прямая есть вертикальная асимптота. В силу симметрии графика также– вертикальная асимптота.

4. Исследуем поведение функции на концах области определения, в бесконечности. Здесь целесообразно рассматривать заданную функцию, как . Поскольку , то прямая — горизонтальная асимптота функции. График функции на концах области определения отличается от на отрицательную бесконечно малую, приближаясь к прямой снизу (рис. 9).

5. Экстремумы и интервалы монотонности. Первая производная исследуемой функции равняется . Тогда . при . При не существует. Однако критической точкой является только точка (так как значения не входят в область определения функции). Поскольку при а при то точка минимума и . На интервалах и функция убывает, на интервалах и – возрастает.

6. Остается выяснить особенности изменения функции на интервалах монотонности, найти области выпуклости , вогнутости, точки перегиба.

.

Очевидно, что на интервале и функция вогнута на этом интервале. На множестве , и на этих интервалах функция выпукла. Точек перегиба нет, поскольку ОДЗ и .

На и , значит, функция убывает все быстрее. В области , а , следовательно, здесь функция убывает все медленнее, пока в точке скорость ее изменения не становится равной нулю. Затем на и , это говорит о том, что функция здесь возрастает все быстрее. На , а , поэтому функция здесь растет все медленнее, приближаясь к своему предельному значению снизу.

Итог исследования – график функции, рис. 9. ◄

Выявить особенности монотонного изменения функции.

116. 117. 118.

119. 120. 121.

122. 123. 124.

125. 126. 127.

Провести полное исследование функции и построить ее график

128.	129.	130.
131.	132.
133. 1)	2)	3)