§ 2. Приложения производной

2.1. Раскрытие неопределенности. Правило Лопиталя. Использование производной позволяет значительно упростить вычисление предела функции.

Если при вычислении предела имеет место неопределенность вида или и существует при , то = . Данное положение известно как правило Лопиталя.

Правило Лопиталя можно при необходимости применять повторно.

Пример1. Найти

 . ◄

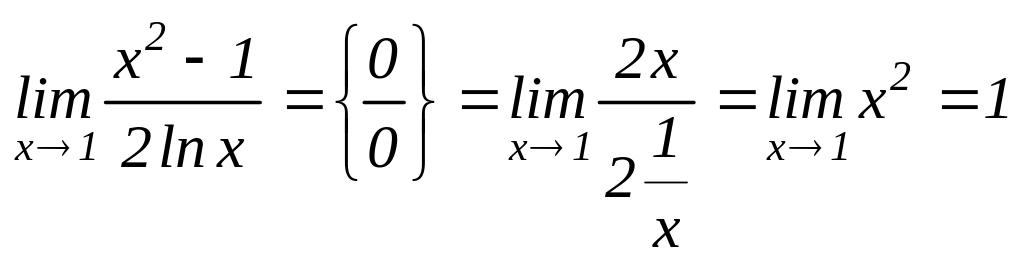Пример2. Найти

 ◄

Найти пределы функций, используя правило Лопиталя.

84. 85. 86.

87. 88а. 88б.

2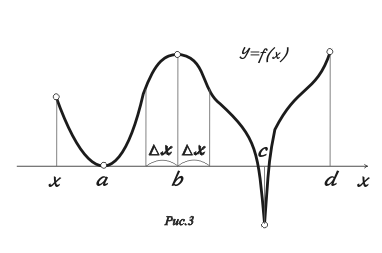 .2. Возрастание и убывание функции. Производная функции дает достаточно простой и удобный способ выявления интервалов ее монотонного изменения. На рис. 3 функция является монотонно возрастающей на интервалах и и монотонно убывающей на и

Если функция возрастает, то согласно определению возрастающей функции, большему значению аргумента соответствует большее значение функции, то есть Следовательно, приращение возрастающей функции всегда положительно, значит Поэтому а поскольку предельное значение неотрицательной переменной также неотрицательно, то первая производная возрастающей функции есть величина неотрицательная Нетрудно доказать, что справедливо обратное. Если то – возрастающая функция.

Итак, если на некотором интервале функция монотонно возрастает, то первая производная функции здесь неотрицательна и наоборот, если то функция возрастает. Аналогичным образом, если на некотором интервале функция монотонно убывает, ее производная здесь неположительна, то есть  и наоборот, если , то функция убывает.

Таким образом, знакопостоянство первой производной на некотором интервале является необходимым и достаточным условием монотонного изменения функции на этом интервале.

В простейших случаях, как на рис. 3, область определения функции можно разбить на конечное число интервалов монотонности. Каждый из интервалов монотонности ограничен особыми, так называемыми, критическими точками, в которых или не существует. На рис. 3 это точки а, и с. Поэтому, чтобы выявить границы интервалов монотонности, достаточно найти, при каких значениях аргумента или не существует. Затем, чтобы установить характер монотонности на выявленных интервалах, достаточно выяснить знак на этих интервалах.

Пример1. Найти интервалы монотонности функции .

► Имеем Очевидно при и при то есть функция убывает на интервале и возрастает на интервале абсцисса вершины параболы . ◄

Заметим, что необходимое условие монотонности описывается нестрогим неравенством. Поскольку, если функция возрастает (убывает) на некотором промежутке , то можно лишь утверждать, что производная функции на этом промежутке неотрицательна (неположительна) : при всяком . То есть в отдельных точках производная монотонной функции может равняться нулю.

Пример2. Найти интервалы монотонности функции

► Найдем производную . Очевидно, что при При производная обращается в нуль. Однако, функция, описывающая кубическую параболу, монотонно возрастает на всей числовой оси. ◄

Итак, обобщая, отметим, если функция возрастает, Функция убывает, если ее производная

2.3. Экстремум функции. Если в окрестности точки выполняется неравенство ( ) , то это означает, что в точке функция имеет наибольшее (наименьшее) значение по сравнению с ее значениями в окрестных точках. Поэтому точка называется точкой максимума (минимума) функции , а – максимумом (минимумом) этой функции. Точки минимума и максимума функции называются точками экстремума.

Заметим, что на рис.3 и . То есть максимум функции, а и – минимумы. При этом экстремальные точки функции являются граничными точками интервалов ее монотонного изменения. Поэтому, проходя через экстремальную точку, первая производная функции меняет знак на противоположный.

Будучи непрерывной, принимает при этом нулевое значение в точках и , и не существует. Таким образом, имеем необходимое условие экстремума: если – точка экстремума функции , то или не существует, то есть точка экстремума – непременно критическая точка этой функции. Обратное верно не всегда. Не всякая критическая точка есть точка экстремума. Поэтому равенство нулю или несуществование первой производной является необходимым условием экстремума, но недостаточным.

Пример1. Найти критические точки функции и убедиться в наличии или отсутствии экстремума в этих точках: а) б) в)

► а) Производная В точке , и действительно, в точке функция имеет экстремум (рис. 4).

б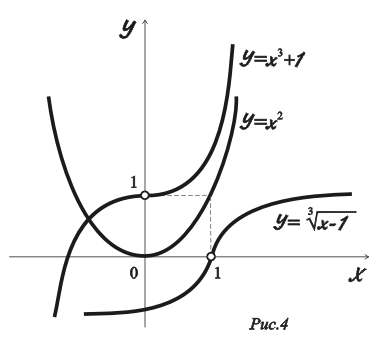 ) Функция возрастает на всей числовой оси по свойству степенной функции. Производная в точке равна нулю, то есть но экстремума в точке нет.

в) Функция также возрастает на всей числовой оси. Производная при не существует, то есть но экстремума в этой точке нет. ◄

Таким образом, для нахождения экстремумов функции требуется дополнительное исследование критических точек. Иными словами, требуется знать достаточные условия экстремума.

Д о с т а т о ч н ы е у с л о в и я э к с т р е м у м а.

П е р в о е д о с т а т о ч н о е у с л о в и е э к с т р е м у м а . Пусть – критическая точка функции . Функция непрерывна в точке и имеет в некоторой окрестности , кроме, быть может , точки , конечную производную. Если переходя через , первая производная меняет знак с «+» на «–» , то если с «–» на «+», то

Если не меняет знака, то экстремума нет.

Таким образом, согласно первому достаточному условию экстремума, критическая точка является экстремальной точкой, если при переходе через эту точку первая производная функции меняет знак, а сама функция – характер монотонности.

Итак, чтобы найти экстремум функции, необходимо сделать следующее:

1) Найти и критические точки, в которых или не существует.

2) Определить знак слева и справа от каждой критической точки и сделать вывод о наличии экстремумов.

3) Вычислить экстремальные значения функции.

Пример2. Исследовать на экстремум функцию

► Поскольку экстремальные точки функции всегда являются критическими точками, найдем последние. В них или не существует.

1. Производная функции

2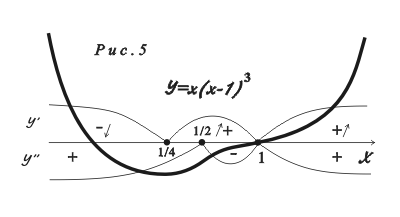 . Приравнивая производную к нулю, находим критические точки функции Точек, в которых производная не существует, у данной функции нет, так как определена на всей числовой оси.

3. Нанесем критические точки на числовую прямую (рис. 5).

Для определения знака производной слева и справа от критической точки выберем, например, значения и и найдем и . Следовательно, при всех и на интервале

Аналогично устанавливаем, что на интервале

Согласно достаточному условию экстремума критическая точка – – точка минимума данной функции. В критической точке экстремума нет.

4. Находим ◄

Иногда для установления характера критической точки удобно использовать в т о р о е д о с т а т о ч н о е у с л о в и е э к с т р е м у м а . Пусть функция дважды дифференцируема в критической точке и в некоторой ее окрестности. Если то – точка максимума функции , если то – точка минимума. Действительно, в окрестности max убывает, меняя знак с «+» на «—» , поэтому В окрестности min меняет знак с «—» на «+», то есть является возрастающей функции, следовательно,

Если же то требуются дополнительные исследования.

Таким образом, согласно второму достаточному условию экстремума, критическая точка является экстремальной точкой, если При имеет место max, при наблюдается min.

Пример3. Производитель реализует свою продукцию по цене ден. ед. за единицу продукции, а издержки при этом пропорциональны кубу выпускаемого объема продукции Найти оптимальный для производителя объем выпуска продукции и соответствующую ему прибыль.

► Будем считать оптимальным объем продукции, обеспечивающий максимум прибыли. Пусть х – объем выпускаемой продукции. Тогда функция прибыли – – где – доход от реализуемой продукции, а – издержки по ее выпуску. Чтобы найти условия, обеспечивающие максимум прибыли, исследуем функцию прибыли на экстремум.

1. Находим

2. Находим критические точки. откуда (вторая критическая точка согласно условию задачи не имеет смысла, так как объем продукции не может быть величиной отрицательной).

3. Далее нужно установить, является ли найденная критическая точка экстремальной. Поскольку численное значение критической точки неизвестно, удобно вместо исследования знака первой производной в окрестности критической точки воспользоваться вторым достаточным условием экстремума. Поэтому найдем вторую производную и исследуем ее знак. . Так как объем продукции может быть только положителен ( ), то всегда при любом . Следовательно, в найденной критической точке функция прибыли имеет максимум.

Заметим, что использование второго достаточного условия экстремума освободило нас от необходимости определять знак в окрестности критической точки.

4. Находим максимум функции прибыли (то есть максимальный размер прибыли) ◄

Замечание. Второе достаточное условие экстремума утверждает, что если в критической точке то в этой точке имеется экстремум. Обратное утверждение, однако, не верно. Экстремум в критической точке может быть и при выполнении условия . Рассмотрим, например, функцию Имеем В критической точке вторая производная также обращается в нуль. Но – точка экстремума, а именно – минимума. Так что в отличие от первого второе достаточное условие является только достаточным, но не является необходимым. Поэтому, если в критической точке то рекомендуется перейти к первому достаточному условию экстремума или исследовать или

В 89 - 105 исследовать функцию на монотонность и экстремумы.

89.	90.	91.
92.	93.	94.
95.	96.	97.
98.	99.	100.
101	102.	103.
104.	105. а)	б)

2.4. Наибольшее и наименьшее значение функции. Наибольшее (наименьшее) значение на отрезке непрерывная функция принимает или в одной из экстремальных точек или на концах отрезка. Поэтому для определения наибольшего (наименьшего) значения функции надо вычислить значения функции во всех критических точках отрезка и на концах отрезка и взять наибольшее (наименьшее) из полученных значений.

Если функция определена и непрерывна на некотором неограниченном промежутке, то среди значений функции может не быть ни наибольшего, ни наименьшего.

Пример1. Найти наибольшее и наименьшее значение функции на указанных промежутках:

а) на отрезке

б) на отрезке

► а) Найдем производную Производная обращается в нуль в двух точках: и . Обе эти точки лежат внутри заданного отрезка , следовательно, обе должны приниматься во внимание. Для отыскания наибольшего и наименьшего значений необходимо вычислить значения функции в критических точках. и на концах отрезка Из полученных данных выбираем наибольшее и наименьшее значение функции на отрезке . Наибольшее значение функции равно наименьшее –

б) Ищем критические точки. при или при то есть при и Но и лежат за пределами заданного отрезка. На заданном отрезке нет критических точек. Остается вычислить значения функции на концах отрезка: Таким образом, есть наименьшее значение функции, а — ее наибольшее значение. ◄

В задачах 106 - 115 найти наибольшее и наименьшее значение функции на заданном отрезке.

106. 107.

108. 109.

110. 111.

112. 113.

114. 115.