3. Изображение синусоидальных функций времени (напряжение, сила тока, мощности) векторами на комплексной плоскости

Расчет сложной разветвленной цепи может быть существенно упрощен, если заменить синусоидальные токи и напряжения векторами, расположенными на комплексной плоскости. Такой метод получил название метода комплексных амплитуд.

В основе данного метода лежит формула Эйлера:

,31(2.24)

где j=.

Умножив обе части на А, получим:

A = A₁+A₂,

где A=модуль комплексного числа;

 аргумент комплексного числа.

Рис.2.17. Изображение векторана комплексной плоскости

( угловая частота вращения вектора)

Поскольку в формуле Эйлера может быть любым, мы сделаем его линейной функцией времени:

 = t + .32(2.25)

Тогда:

.33(2.26)

Полученный результат ( 2 .27) показывает, что синусоидальная функция времени есть мнимая часть некоторого комплексного числа:

а = Asin(t +) = I_mAe^j(t+); 34(2.27)

при условии, что t= 0 получим:

=A35(2.28)

Векторная диаграммадиаграмма векторов на комплексной плоскости, построенная с учетом их взаимной ориентации по фазе.

Если вектора вращаются на плоскости с одинаковыми частотами , то их взаимное положение не меняется, это свойство позволяет исключить из рассмотрения сам факт их вращения, то есть приниматьt = 0.

В качестве примера на Рис. 2 .18 изображена операция умножения некоторого вектора на оператор поворотаj.

Пусть модуль =10А. Его положение на комплексной плоскости зависит от значения аргумента. Значениям =0, 90⁰,  90⁰соответствуют комплексные числа:

;;.

По формуле Эйлера:

;

;

;

;

Рис.2.18. Умножение вектора на+jи–j

4. Основы символического или комплексного расчета цепей синусоидального тока

Этот метод позволяет перейти от дифференциальных уравнений, составленных для мгновенных токов, напряжений и т.д., к алгебраическим уравнениям, составленных для соответствующих им комплексных изображений.

1.Последовательное соединение

Рис.2.19. Последовательное соединениеR, L, C

На основании второго закона Кирхгофа:

u = u_R + u_L + u_C;

u = iR +L+.36(2.29)

Перейдем к комплексным изображениям:

i = I_msin(t+_i)  _. 37(2.30)

Используя полученный комплекс тока, определим комплексы падения напряжения на участках цепи:

Для сопротивления:

, (2.31)

где . 38

Для индуктивности:

.39(2.32)

Для емкости:

.40(2.33)

Найденные комплексы U_R,U_C,U_L, подставим в исходное уравнение:

,41(2.34)

.42(2.35)

 закон Ома в комплексной форме.

Выражение в знаменателе представляет собой комплексное сопротивление исходной цепи, которое имеет вещественную и мнимую составляющую.

,43(2.36)

где ; .

Для комплексных амплитуд закон Ома запишется в следующем виде:

,44(2.37)

где U_m= I_mzамплитуда напряжения;

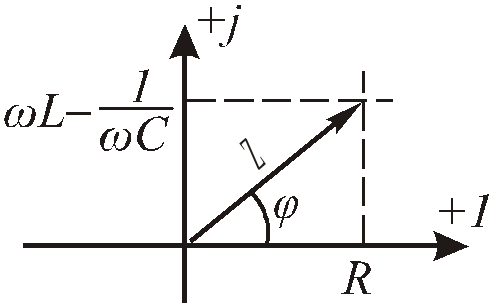
Рис.2.20. Изображение сопротивления на комплексной плоскости

φ_U =  + _i;   = _U – _i; 45(2.38)

u(t) = U_msin(t + _U). 46(2.39)

Построим векторную диаграмму цепи.

Рис.2.21. Векторная диаграмма для последовательного колебательного контура

i(t) = I_msin(t + _i); _i > 0.

Построение векторной диаграммы начинают с вектора тока, т.к. он одинаков на всех участках цепи. Из построенной на комплексной плоскости векторной диаграммы можно выделить векторный треугольник напряжений, представленный на Рис. 2 .22.

Рис.2.22. Векторный треугольник напряжений

Ниже приведен треугольник сопротивлений.

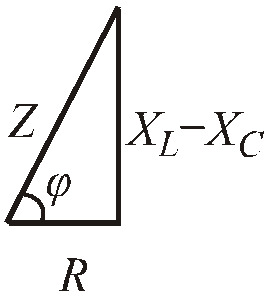
Рис.2.23. Скалярный треугольник сопротивлений

Угол сдвига фаз между током и напряжением можно определить из любого треугольника.

.47(2.40)