Задание для самостоятельной работы:

• Проведите кластерный анализ своего файла с наблюдениями.

• Попробуйте строить решения с разными критериями, мерами сходства и методами кластеризации.

• Рассмотрите получающиеся дендрограммы и сделайте геолого-экологические выводы о группах наблюдений.

• Сохраните различные решения и проведите их интерпретацию.

• Постройте классификацию переменных экспертной оценки, выбрав в качестве меры сходства коэффициент корреляции Пирсона.

• Попробуйте преобразовывать меру сходства, манипулируя знаком.

Лабораторная работа №7

Факторный анализ

Факторный анализ занимает особое место в экологии, являясь одним из наиболее популярных многомерных методов анализа данных. Цель факторного анализа состоит в объяснении интеркорреляций между наблюдаемыми переменными минимальным числом непосредственно ненаблюдаемых причин — факторов. В этом смысле назначение факторного анализа совпадает с целью любого научного исследования — отысканием экономного объяснения наблюдаемого многообразия явлений. С помощью факторного анализа в конкретном исследовании обычно решаются следующие задачи:

1. Уменьшение размерности данных. Поскольку изучаемые объекты можно характеризовать бесконечным числом разнообразных признаков, то полезной бывает группировка признаков по смысловому сходству. Таким образом, появляется возможность описания объектов меньшим числом независимых параметров. Такое уменьшение размерности пространства признаков помогает устранить дублирование информации, исключив малоинформативные или "шумящие" переменные.

2. Объяснение разложением на составляющие. Используя регрессионный анализ, мы уже видели, как можно наблюдаемое значение зависимой переменной разложить на компоненты, соответствующие независимым переменным. Факторный анализ идет в этом отношении еще дальше и позволяет нам расчленить не только значение любого признака у испытуемого на части, но и дисперсию отдельной переменной или корреляцию между ними, приписав каждую часть действию косвенно проявляющих себя факторов.

3. Косвенное измерение. Факторный анализ базируется на предположении о том, что корреляция наблюдаемых переменных объясняется существованием какой-то стоящей за ними общей причины (или нескольких причин). Таким образом, наблюдаемые переменные рассматриваются в качестве косвенных индикаторов так называемых латентных переменных (т.е. переменных, которые непосредственно не измеримы). Факторный анализ позволяет не только получить информацию, помогающую нам идентифицировать латентные переменные, но и дает способ количественно оценить значение латентной переменной на исследуемом объекте.

Рассмотрим на небольшом примере особенности проведения факторного анализа и интерпретации его результатов. Для иллюстрации выбран небольшой фрагмент геохимических данных одного из объектов. Пусть исследованию подвергается изучение связей четырех пар элементов (дескрипторов), относящихся к двум факторам – халькофильным (V01, V06) и сидерофильным (V02, V07) геохимическим группам. Интеркорреляции между ними представлены в следующей таблице

Correlation Matrix:

V01 V06 V02 V07

V01 1.00000

V06 .79582 1.00000

V02 -.31784 -.43264 1.00000

V07 -.42345 -.45176 .82720 1.00000

Как видим, наибольшие корреляции наблюдаются между дескрипторами, относящимися к одному фактору. После того, как получена корреляционная матрица, необходимо ее объяснить через действие скрытых переменных — факторов. Мы уже знаем, что причиной корреляции наблюдаемых переменных является близость геохимических свойств элементов одной группы. Соотношения наблюдаемых переменных и четырех латентных переменных (факторов) представлены в таблице, которая называется матрицей факторного отображения (или матрицей факторных нагрузок):

Factor Matrix:

Factor 1 Factor 2 Factor 3 Factor 4

V01 -.77820 .55062 -.25716 .15839

V06 -.82582 .45790 .29541 -.14522

V02 .79794 .53432 -.17058 -.22066

V07 .83788 .45386 .21477 .21413

Числа, стоящие на пересечении строк и столбцов, называются нагрузками (loadings) переменных на факторы. Нагрузка — это фактически регрессионный коэффициент, который показывает, какой вес имеет данный фактор для предсказания значения соответствующей переменной у испытуемого. Например, для предсказания признака V01 получим следующее регрессионное уравнение:

V01 = -0.77820*F1 + 0.55062*F2 -0.25716*F3 + 0.15839*F4.

Пока что мы не знаем, что это за факторы и как получить их значение на объекте. Из уравнения видно, что наибольшее влияние на переменную оказывает первый фактор, при его увеличении значение V01 уменьшается.

Каким же образом матрица факторного отображения позволяет нам "объяснить" рассмотренную выше корреляционную матрицу? Согласно модели факторного анализа корреляцию между переменными можно получить, суммируя произведения их нагрузок на факторы. Например, чтобы воспроизвести корреляцию переменных V01 и V06, необходимо взять произведение их нагрузок на первый фактор, прибавить к нему произведение нагрузок на второй, третий и четвертый факторы:

R(V01, V06) = (-0.77820)*(-0.82582) + (0.55062)*(0.45790) + (-0.25716)*(0.29541) + (0.15839)*(-0.14522) = 0.79581.

Как видим, полученное значение с точностью до ошибок округления соответствует наблюдаемой корреляции переменных V01 и V06. Иными словами, модель факторного анализа позволила нам восстановить коэффициент корреляции между переменными, зная их соотношение с факторами.

Если перемножить нагрузки, то выражение примет следующий вид:

R(V01, V06) = 0.64265 + 0.25213 - 0.07597 - 0.02300 = 0.79581.

Каждый компонент суммы представляет ту часть корреляции, которая объясняется соответствующим фактором. Мы видим, что первый фактор "объясняет" наибольшую часть: 0.64265 из 0.79581. На второй фактор приходится меньшая часть 0.25213. Третий и четвертый факторы вместе определяют всего лишь -0.09897 и их влиянием можно пренебречь.Таким образом, нам удалось разложить коэффициент корреляции на компоненты и объяснить каждый из них действием определенной латентной переменной. Осталось только показать, каким образом раскладывается на части дисперсия переменной. В факторном анализе все переменные подвергаются стандартизации (делятся на стандарт), а дисперсия стандартизированной переменной всегда равна 1. Чтобы выразить единичную дисперсию переменной в виде суммы компонент, необходимо возвести нагрузки данной переменной на все факторы в квадрат и полученные значения сложить.

Например, для дисперсии переменной V01 = (-0.77820)² + (0.55062)² + (-0.25716)² + (0.15839)² = 0.6056 + 0.3032 + 0.0661 + 0.0251 = 1.0000

Из полученного выражения видно, что наибольший вклад в вариацию переменной V01 вносит первый фактор (он объясняет 60.56% ее дисперсии). На второй фактор приходится 30.32%, а третий и четвертый вместе объясняют лишь 9.12%.

Рассмотрев способ, по которому в факторном анализе происходит разложение на различные причины, мы не сократили размерность признакового пространства: ведь от совокупности из четырех наблюдаемых переменных мы перешли к системе из четырех факторов. Но мы убедились, что одни факторы являются более важными, другие — менее существенными для объяснения отдельных переменных или их корреляций. Однако нам необходим какой-то показатель, с помощью которого можно было бы характеризовать вес (важность) фактора для объяснения всей совокупности переменных, включенных в анализ. В качестве такого показателя используют сумму квадратов нагрузок всех переменных на данный фактор. Этот показатель, вычисленный для факторного отображения до проведения вращения, носит название собственного значения фактора (eigenvalue). В следующей таблице приведены собственные значения для всех четырех факторов, причем факторы упорядочены по величине собственного значения:

Factor Eigenvalue Pct of Var Cum Pct

1 2.62632 65.7 65.7

2 1.00434 25.1 90.8

3 .22862 5.7 96.5

4 .14072 3.5 100.0

Собственное значение для первого фактора получено следующим образом: 2.62632 = (-0.77820)² + (-0.82582)² + (0.79794)² + (0.83788)².

Для того, чтобы легче было судить об относительной важности фактора, собственные значения выражают в виде процента объясненной дисперсии всей совокупности переменных. Поскольку все переменные стандартизированы и дисперсия каждой равна 1, полная дисперсия совокупности из m переменных равна m. В нашем случае полная дисперсия составляет 4. Соответственно для получения доли полной дисперсии первого фактора необходимо вычислить 2.62632 ÷ 4.00000 × 100 = 65.7%.

Таким образом, вклад данного фактора в объяснение совокупной дисперсии составляет 65.7%, что сразу дает представление о его важности. Процент объясненной дисперсии приведен в таблице под заголовком Pct of Var (Percent of Variance — процент дисперсии). Из этой таблицы мы узнаём, что второй фактор объясняет 25.1%. Вместе первый и второй факторы объясняют 90.8% совокупной дисперсии (накопленная часть дисперсии указана в таблице под заголовком Cum Pct). Оставшиеся факторы соответственно объясняют гораздо меньшую долю: 9.2%. Отсюда следует вывод: можно пожертвовать данными факторами для сокращенного описания соотношения переменных. Если мы отбросим эти факторы, то потеряем часть информации, содержащейся в корреляционной матрице, однако зато выиграем в другом отношении — сможем рассматривать всего две основные причины, стоящие за корреляциями переменных.

Когда мы уменьшаем количество факторов, объяснение дисперсий переменных и их корреляций становится неточным — ведь часть информации потеряна вместе с исключенными факторами. В следующей таблице вы увидите информацию о доле дисперсии переменных, объясненных общими факторами — так называемую "общность" (англ. communality):

Final Statistics:

Variable Communality * Factor Eigenvalue Pct of Var Cum Pct

V01 .90878 * 1 2.62632 65.7 65.7

V06 .89165 * 2 1.00434 25.1 90.8

V02 .92221 *

V07 .90802 *

Как видим, уменьшение числа факторов вдвое привело к весьма незначительной потере информации: полнота объяснения дисперсии отдельных переменных составляет 89-92%, а в целом оставшиеся факторы объясняют 90.8% совокупной дисперсии.

Для того, чтобы увидеть, насколько хорошо оставшиеся факторы воспроизводят (reproduce) наблюдаемые корреляции между переменными, в SPSS можно заказать вывод специальной матрицы:

Reproduced Correlation Matrix:

V01 V06 V02 V07

V01 .90878* -.09897 .00891 -.02131

V06 .89478 .89165* -.01835 .03235

V02 -.32675 -.41429 .92221* -.08389

V07 -.40213 -.48411 .91108 .90802*

В этой матрице элементы, находящиеся на диагонали, представляют собой общности переменных (обозначены звездочками), ниже диагонали выведены воспроизведенные корреляции, выше диагонали — остаточные коэффициенты. Например, наблюдаемая корреляция между 1 и 6 переменной, как мы уже видели, равна 0.79582. Два первых фактора воспроизводят между ними корреляцию 0.89478 (первый столбец, вторая строка). Остаточная корреляция (разница между наблюдаемой и воспроизведенной) равна -0.09897 (второй столбец, первая строка). Совершенно очевидно, что если наблюдаются большие остаточные корреляции, это указывает на неадекватность модели с данным числом факторов. Иногда плохо объясняются лишь отдельные связи, тогда следует пересмотреть включение тех или иных признаков в состав анализируемых переменных.

Решение о количестве извлекаемых факторов является чрезвычайно важным при проведении анализа. От этого решения зависит, с одной стороны, полнота воспроизведения наблюдаемых корреляций, а с другой — содержательная интерпретация модели. Существует несколько основных способов, опираясь на которые можно оценить количество факторов в конкретном исследовании:

• Критерий Кайзера. Оставлять факторы, собственное значение которых превышает 1.0. Логика этого критерия проста: вариация отдельной переменной равна единице, поэтому не представляет интереса фактор, объясняющий меньшую долю совокупной дисперсии. Несмотря на то, что этот критерий установлен в пакете SPSS по умолчанию, в литературе он подвергается обоснованной критике. Как показали модельные эксперименты, данный критерий недооценивает число факторов при небольшом количестве переменных и переоценивает - при большом.

• Второй способ состоит в том, что оставляют столько факторов, сколько объясняют заранее фиксированную часть совокупной дисперсии — например, 70-80%.

• В состав методов выделения факторов пакета SPSS входят метод максимального правдоподобия (maximum likelihood) и обобщенный метод наименьших квадратов (generalized least squares). Их особенностью является возможность проверки статистической гипотезы о числе факторов — сравнение наблюдаемой и воспроизведенной матриц производится с целью определения случайности остатков. Ниже приведен фрагмент распечатки для проверки адекватности 4-факторной модели:

Test of fit of the 4-factor model:

Chi-square statistic: 7.0587, D.F.: 11, Significance: .7943

Для проверки нулевой гипотезы используется критерий хи-квадрат. Если его значимость (Significance) оказывается меньше установленной границы (скажем, 0.05), нулевую гипотезу отвергают — в этом случае расхождение между наблюдаемой и воспроизведенной матрицами считается неслучайным. К сожалению, эти методы очень чувствительны к проблеме вырожденности корреляционной матрицы.

• Четвертый, эвристический способ, предложен Р.Кеттелом. Этот способ базируется на анализе специального графика, на котором изображается зависимость величины собственного значения фактора от его номера. График получил название Scree Plot (диаграмма осыпи), поскольку напоминает склон горы.

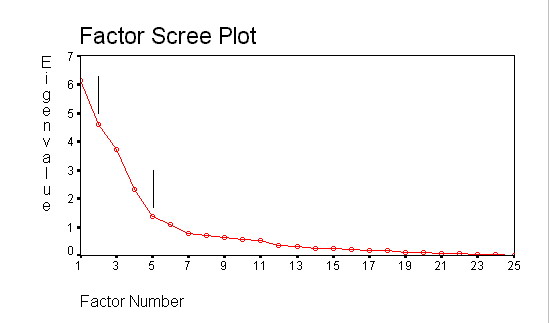
Рисунок 26 Зависимость собственных значений факторов

"Скальная" часть соответствует реально существующим факторам, осыпь "осколков" у подножия — статистическому шуму. Обычно кривая на графике имеет несколько точек перегиба (на рисунке отмечены черными вертикальными линиями). Р.Кеттел показал, что оптимальное число факторов можно выделить по точке второго перегиба.

Проблема определения числа факторов — только одна из многих в факторном анализе. Другая проблема состоит в том, что существует бесконечное множество решений, одинаково хорошо объясняющих одну и ту же корреляционную матрицу. В этих условиях необходим какой-то дополнительный критерий, с помощью которого можно среди множества эквивалентных решений выбрать единственное. Таким критерием является принцип "простой структуры". Более простой для интерпретации является такая матрица факторного отображения, в которой нагрузки переменных на факторы равны или 0, или 1, т.е. фактор либо определяет переменную, либо нет. Например, факторное отображение случая, рассмотренного ранее, можно изобразить в виде следующей диаграммы рассеивания, на которой переменные размещаются в пространстве, заданном факторами (рис. 27). Координаты точек-переменных определяются их нагрузками на факторы.

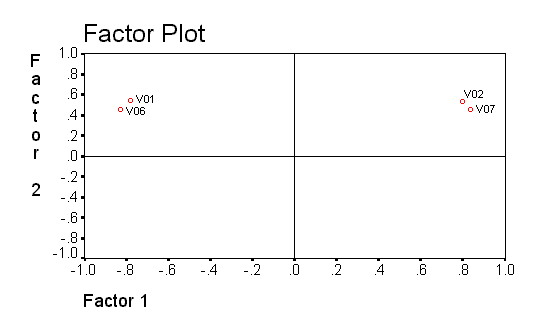
Рисунок 27. Диаграмма рассеяния факторов

Как видим, для объяснения каждой переменной нам необходимо привлекать оба фактора — все нагрузки в матрице существенно отличаются от 0, и точки переменных находятся вдали от осей-факторов. Однако если "повернуть" конфигурацию из точек вокруг начала координат по часовой стрелке на некоторый угол, можно получить картину, показанную на следующей диаграмме (рис.28):

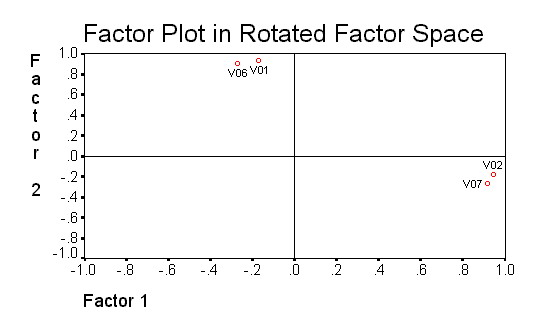
Рисунок 28. Диаграмма рассеяния факторов после вращения

Такое «повернутое» решение соответствует матрице факторного отображения, которая столь же хорошо воспроизводит наблюдаемые корреляции переменных, как и рассмотренная ранее. Однако у данного решения есть преимущество простоты: для объяснения переменной требуется минимальное число причин (точки переменных находятся вблизи соответствующих осей). Матрица нагрузок переменных после вращения приводится ниже:

Rotated Factor Matrix:

Factor 1 Factor 2

V01 -.16985 .93805

V06 -.26878 .90521

V02 .94378 -.17744

V07 .91593 -.26284

Отличие этой матрицы от рассмотренной ранее состоит в том, что она легче интерпретируется, поскольку факторы оказывают влияние на специфическую группы переменных. Теперь отчетливо видно, что переменные V01 и V06 определяются действием одного фактора, а V02 и V07 — второго. Иногда для повышения четкости структуры подавляют вывод небольших нагрузок, что облегчает анализ матрицы факторного отображения:

Factor 1 Factor 2

V01 .93805

V06 .90521

V02 .94378

V07 .91593

Помимо повышения интерпретируемости нагрузок, вращение приводит также к более устойчивым результатам при изменении состава переменных или выборки наблюдений.

Существуют различные подходы к определению простой структуры и соответственно различные методы вращения. Наиболее популярными в настоящее время являются методы ортогонального вращения (т.е. такого, который сохраняет прямые углы между факторами): варимакс, эквамакс, квартимакс. Различие между ними состоит в том, что варимакс стремится упростить интерпретацию факторов, квартимакс — переменных, а эквамакс — и факторов, и переменных одновременно.

В отличие от ортогональных методов, методы косоугольного вращения не сохраняют независимость факторов. При таком вращении оси факторов проводят так, чтобы они проходили как можно ближе к пучкам переменных, при этом может оказаться, что перпендикулярность осей координат может быть нарушена — появляется корреляция между самими факторами. Косоугольное решение упрощает модель, поскольку позволяет добиваться более простой структуры, однако и усложняет ее, так как вводит в рассмотрение ненаблюдаемые связи между латентными переменными.

Некоторые авторы предпочитают применение косоугольного вращения по той причине, что такой подход не накладывает никаких априорных ограничений на факторное решение. В пакете SPSS имеется всего один метод косоугольного вращения — облимин. Задавая различные значения его параметра дельта, можно регулировать степень косоугольности получаемого решения. При использовании косоугольного метода наряду с матрицей факторного отображения мы получаем еще матрицу корреляций между факторами. Кроме того, для интерпретации также выводится матрица корреляций между переменными и факторами, называемая факторной структурой. Для нашего примера с четырьмя переменными эти матрицы выглядят следующим образом:

Pattern Matrix:

Factor 1 Factor 2

V01 .05066 .97442

V06 -.06481 .91406

V02 .97875 .04389

V07 .92718 -.05567

Structure Matrix:

Factor 1 Factor 2

V01 -.37654 .95221

V06 -.46554 .94247

V02 .95951 -.38521

V07 .95159 -.46216

Factor Correlation Matrix:

Factor 1 Factor 2

Factor 1 1.00000

Factor 2 -.43841 1.00000

Как видим, факторное отображение (Pattern Matrix) при косоугольном вращении в наибольшей степени соответствует принципу простой структуры: влияние фактора на переменную или минимальное, или максимальное. При этом оказывается, что наши факторы имеют слабую связь, равную -.43841. Согласно основной модели факторного анализа наблюдаемые корреляции переменных можно объяснить их нагрузками на факторы и корреляциями между факторами.

Интерпретация факторов предполагает поиск обобщенного названия для группы нагружающихся на него переменных. Иногда найти то общее, что проявляет себя через корреляцию переменных совсем непросто, и требует от исследователя развитой способности к обобщению. Особенно затрудняет интерпретацию то, что переменные могут иметь несколько оснований сходства, и анализ должен исключить альтернативные объяснения, разведя их по разным факторам. Часто уже при планировании исследования с применением факторного анализа в набор анализируемых признаков включают так называемые маркерные переменные (т.е. такие индикаторы факторов, которые в предыдущих исследованиях показали свою устойчивую связь с ними.)

Проблема измерения факторов. После того, как исследователь получил удовлетворительное факторное решение, — простое, экономное, интерпретируемое, — следующим естественным желанием является попытка измерения значения латентных переменных. Поскольку они непосредственно не наблюдаются, точно измерить их невозможно, можно произвести лишь косвенную оценку. Для этого требуется получить матрицу так называемых факторных коэффициентов. Факторные коэффициенты являются коэффициентами множественного уравнения регрессии при предсказании факторов на основании стандартизированных значений наблюдаемых переменных. В примере с четырьмя переменными матрица факторных коэффициентов выглядит следующим образом:

Factor Score Coefficient Matrix:

Factor 1 Factor 2

V01 .17246 .59885

V06 .09486 .54565

V02 .58947 .16697

V07 .54421 .09913

Чтобы получить оценку факторов, надо вычислить следующие выражения, связывающие стандартизированные переменные с факторами:

COMPUTE F1 = zv01*0.17246+zv06*0.09486+zv02*0.58947+zv07*0.54421.

COMPUTE F2 = zv01*0.59885+zv06*0.54565+zv02*0.16697+zv07*0.09913.

EXECUTE .

Пакет SPSS не только выводит матрицу факторных коэффициентов, но и позволяет сохранить оценки значений факторов в виде новых переменных, которые можно использовать в других процедурах.

После теоретической подготовки к факторному анализу, перейдем к его практической реализации. Для вызова процедуры факторного анализа следует в главном меню пакета выбрать последовательность команд Statistics | Data Reduction | Factor. На экране появится главное окно процедуры:

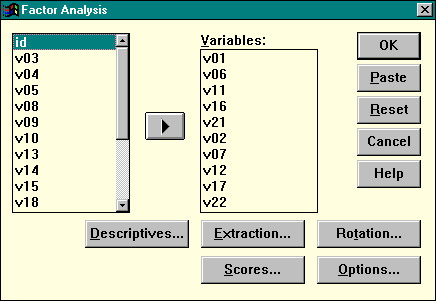
Рисунок 29. Диалоговое окно факторного анализа

Перенесите анализируемые переменные в список Variables. Дополнительные диалоговые окна позволяют установить параметры анализа и заказать вывод дополнительных статистик. Нажатие кнопки Descriptives вызывает появление следующего окна:

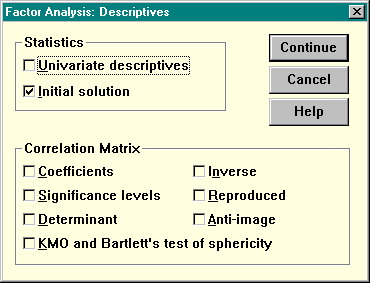
Рисунок 30 Вывод дополнительных статистик при факторном анализе

Здесь флажок Coefficients — вывод матрицы коэффициентов корреляции, и флажок Reproduced — вывод матрицы воспроизведенных и остаточных кореляций.

Диалоговое окно Extraction (извлечение факторов) позволяет установить метод извлечения (список Method), вывести график осыпи (Display: Scree Plot), определить, сколько факторов следует извлечь (если в группе Extract переключатель стоит в позиции Eigenvalues over, испрользуется критерий Кайзера, если же в позиции Number of factors — можно ввести число извлекаемых факторов в поле)

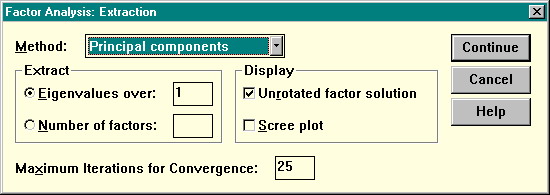
Рисунок 31. Диалоговое окно извлечения факторов

Диалоговое окно Rotation (вращение) дает возможность установить метод вращения факторного решения. По умолчанию вращение не производится (Method: None). Методы варимакс, квартимакс и эквамакс являются ортогональными, прямой облимин — косоугольным. Из ортогональных методов чаще всего применяется варимакс.

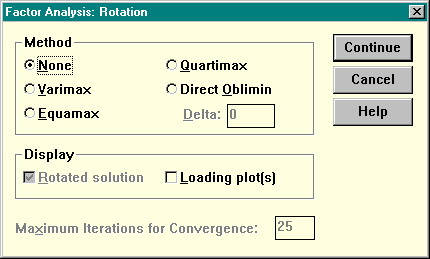
Рисунок 32. Диалоговое окно вращения факторов

Диалоговое окно Scores позволяет заказать сохранение факторных баллов в виде новых переменных (установите флажок Save as variables) и вывести матрицу факторных коэффициентов (флажок Display factor score coefficient matrix). При вычислении факторных баллов возможно использование разных методов их оценок (регрессионный, Бартлетта, Андерсона-Рубина).

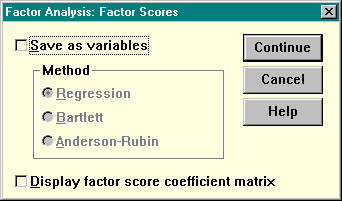
Рисунок 33 Диалоговое окно сохранение факторных баллов

Диалоговое окно Options может быть полезно для облегчения анализа матриц нагрузок.

Рисунок 34 Диалоговое окно опций факторного анализа

Установите флажок Suppress absolute values less than (Подавить вывод значений, меньших по абсолютной величине чем...) и введите граничный коэффициент в поле, чтобы пакет выводил только значительные нагрузки. Чаще всего используются значения 0.2 — 0.3. Флажок Sorted by size (сортировать нагрузки по величине) позволит уделять внимание объяснению наиболее существенных факторов.

Задание для самостоятельной работы:

• Проведите факторный анализ своей матрицы корреляций по переменным V01 — V25 (в качестве методы извлечения факторов выберите метод главных компонент, вращения — варимакс, определение числа факторов по критерию Кайзера).

• Попробуйте ограничить число факторов

• Проинтерпретируйте полученные факторы.