5.2 Множественная линейная регрессия

Парная регрессия позволяет предсказывать значения зависимой переменной, опираясь только на одну независимую переменную. Однако в реальной жизни трудно ожидать столь однозначной и простой зависимости. Большинство природных явлений обусловлено совместным действием множества факторов. Поэтому в данной работе мы воспользуемся множественной регрессией, для того, чтобы построить модель, связывающую прогнозную оценку по одной из переменных (зависимой) с другими, имеющими достаточно тесную связь с нею. Выберите из файла исходных данных ту переменную, с которой вы установили максимальное число корреляций. Попытайтесь объяснить, почему наблюдаются именно эти взаимосвязи. Это необходимо для получения реальной, практической регрессионной модели, которую будет легко интерпретировать.

Теперь построим модель множественной линейной регрессии. Для этого выберите команду Statistics | Regression | Linear, перенесите в поле Dependent имя выбранной зависимой переменной, а в список Independent(s) - все выбранные независимые. Можно установить дополнительные опции: в списке Method установите значение Stepwise ("пошаговый метод формирования оптимального уравнения"). В дополнительном диалоговом окне, вызываемом нажатием кнопки Statistics установите флажок Block Summary (подавление вывода результатов, получаемых на промежуточных шагах построения наилучшего уравнения). В дополнительном окне Save New Varaibles, которое вызывается нажатием кнопки Save установите также: флажок Unstandardized в группе Predicted Values (сохранение значений, предсказанных на основании регрессионной модели), флажки Machalanobis и Cook's в группе Distances (меры необычности и влиятельности отдельных наблюдений).

После нажатия кнопки ОК в окне процедуры регрессионного анализа в окно распечатки будут выведены результаты, смысл которых мы сейчас проанализируем. Прежде следует отметить наиболее существенные отличия этого способа анализа данных. В отличие от предыдущего раза, мы включили в уравнение все имеющиеся у нас предикторы. Однако цель исследователя — не просто получить модель зависимости, а иметь наиболее простую, но объясняющую 100% вариации зависимой переменной. Поэтому мы и установили опцию, заставляющую программу найти минимальный набор предикторов, объясняющий значительную долю вариации отклика. Программа последовательно пробует предикторы один за другим и вставляет их в уравнение. Иногда добавление какой-то независимой переменной приводит к тому, что ранее включенный в модель предиктор теряет свою предсказательную силу. В этом случае программа исключает его из уравнения. Весь процесс продолжается до тех пор, пока не останется ни одного предиктора, который стоит включить в уравнение или исключить из него. Ниже прведена последовательность формирования оптимального уравнения:

Step MultR Rsq F(Eqn) SigF Variable BetaIn

1 ,4269 ,1822 5,125 ,033 In: E.A1 ,4269

2 ,6216 ,3864 6,927 ,005 In: B.A1 -,4535

Как видите, всего программе понадобилось два шага, чтобы построить наилучшее уравнение. Для характеристики каждого шага выводится множественный коэффициент корреляции, достигнутый на нем, его квадрат, F-статистика и ее значимость для проверки гипотезы о равенстве нулю множественного коэффициента корреляции. В конце приведена информация о том, какие переменные были добавлены (IN) или (Out) исключены.

Затем идет блок, уже знакомый вам по предыдущей работе: оценка качества подбора модели.

Multiple R ,62162

R Square ,38641

Adjusted R Square ,33063

Standard Error 1,30392

Analysis of Variance

DF Sum of Squares Mean Square

Regression 2 23,55559 11,77779

Residual 22 37,40441 1,70020

F = 6,92730 Signif F = ,0046

В данном случае надо брать величину, обозначенную на распечатке Adjusted R Square — "скорректированный" квадрат множественной корреляции. Коррекция производится по количеству предикторов, отобранных в конечную, оптимальную модель. Как видите, в этом примере удалось объяснить вариацию в оценке зависимой переменной значениями предикторов на 33%. Судя по значимости F, эта величина скорее всего указывает на то, что и в генеральной совокупности она имеет место.

Следующий блок описывает коэффициенты модели для двух предикторов, их стандартизованные значения и уровень значимости. Величина коэффициента при каждой независимой переменной отражает степень ее влияния на зависимую.

------------------ Variables in the Equation ------------------

Variable B SE B Beta T Sig T

E.A1 ,020716 ,007468 ,464933 2,774 ,0111

B.A1 -,347187 ,128312 -,453480 -2,706 ,0129

(Constant) 4,865158 1,388524 3,504 ,0020

Последняя порция информации содержится в таблице данных. Мы заказали сохранение нестандартизованных предсказанных значений для всех наблюдений. Эти данные сохраняются в новых переменных с префиксом PRE_. Мы сохраняли в таблице еще два дополнительных признака, представляющих особый интерес. Расстояние Махаланобиса — показывает, насколько отклоняется конкретное наблюдение от среднего значения по всем предикторам одновременно, т.е. это мера уникальности наблюдения по сочетанию значений по всем предикторам. Расстояние Кука — это мера влиятельности данного наблюдения. Дело в том, что некоторые наблюдения могут искажать уравнение регрессии, оттягивая на себя ее линию. Обнаружить это легче всего по значениям расстояния Кука.

Задание для самостоятельной работы:

1. Постройте несколько уравнений множественной регрессии и объясните их содержательно.

2. Сравните их по точности, количеству независимых переменных и вкладу каждой из них в модель.

3. Обоснуйте оптимальность одного из уравнений.

5.3 Нелинейная регрессионная модель

Мы познакомились с линейной регрессией. Однако этот метод не является универсальным. В частности, если зависимая переменная является дихотомической (т.е. может принимать только два значения), линейная регрессия неприменима. Между тем дихотомический критерий представляет значительный интерес как при проведении научных исследований, так и в практическом плане. Кроме того, между исходными показателями может существовать нелинейная связь, поэтому необходимо построить нелинейное уравнение регрессии. В этих случаях может использоваться такой малоизвестный у нас метод, как логистическая регрессия. Он обладает следующими достоинствами:

• с его помощью можно оценивать вероятность того, что событие наступит для конкретного испытуемого

• в качестве предикторов допускается использование всех типов переменных, в том числе категориальных.

• модель является нелинейной, в нее можно включать взаимодействия предикторов

Уравнение логистической регрессии имеет следующий вид:

• запись Prob(event) означает "вероятность наступления события".

• e — основание натуральных логарифмов 2.71...

• параметр Z = B₀+B₁*X₁+B₂*X₂+... +B_n*X_n

Зависимость, связывающая вероятность события и величину Z, показана на следующем рисунке:

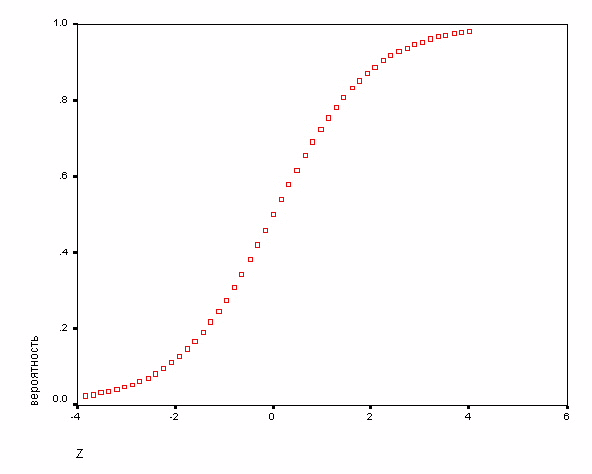
Рисунок 15. Накопленная вероятность наступления события.

Как видите, эта зависимость носит нелинейный характер, причем P не может выходить за пределы диапазона 0 — 1.

Построение модели. В главном меню выберите команду Statistics | Regression | Logistic. На экране появится следующее диалоговое окно (рис. 16).

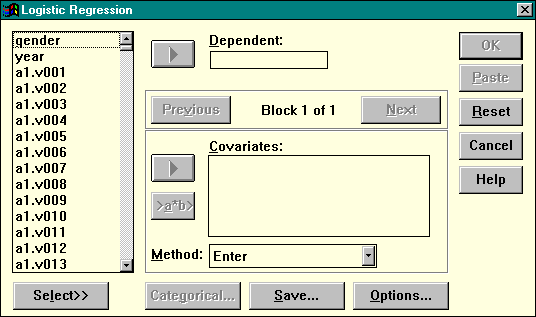
Рисунок 16. Диалоговое окно нелинейной логистической регрессии

Перенесите в поле Dependent дихотомическую переменную, для которой необходимо построить модель предсказания. В список Covariates перенесите независимые переменные (предикторы) кнопкой переноса с треугольной стрелкой. Если вас интересуют взаимодействия предикторов в их влиянии на зависимую переменную, выделите их в левом списке и добавьте в список Covariates с помощью кнопки переноса >a*b>. Если предикторов много, и вас интересует построение оптимального уравнения регрессии, в выпадающем списке Method установите любое значение, отличное от Enter.

Лабораторная работа №6

Кластерный анализ

В данной работе мы рассмотрим метод, с помощью которого исследователь может обнаруживать и описывать реально существующие группы сходных между собой объектов. Рассмотрим простой пример, который поможет нам разобрать понятие сходства и особенности процедуры быстрого кластерного анализа. Например, когда мы строили диаграммы рассеивания, то иногда получается, что совокупность наблюдений распадается на три хорошо различимых группы (кластеры"):

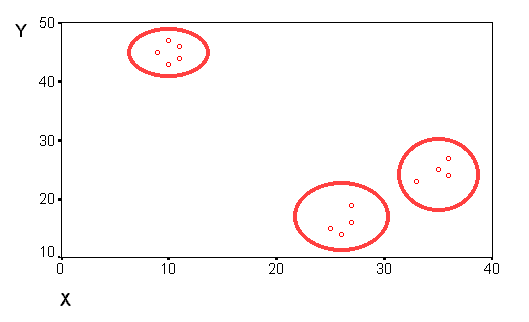
Рисунок 17. Группировка наблюдений на диаграмме рассеяния

Объекты внутри кластера более "похожи" друг на друга, чем на объекты из других групп. На графике точки, обозначающие объекты кластера, находятся на плоскости в непосредственной близости друг от друга, рядом. Таким образом, понятия "сходства" и "пространственной близости" оказываются в каком-то смысле тождественными. Сходство между объектами можно "определить", измеряя расстояние между точками на графике. Известен способ вычисления евклидова расстояния между двумя точками i и j на плоскости, когда известны их координаты X и Y:

Таким образом, чтобы узнать расстояние между двумя точками, надо взять разницу их координат по каждой оси, возвести ее в квадрат, сложить полученные значения для всех осей и извлечь квадратный корень из суммы. Этот способ годится не только для измерения расстояния на плоскости, но и в том случае, когда осей больше: сумма квадратов разниц координат состоит из стольких слагаемых, сколько осей (измерений) в нашем пространстве. Если измеряется сходство объектов по трем признакам, мы имеем дело с трехмерным пространством (его легко представить), если шесть — с шестимерным пространством (которое представить себе гораздо сложнее).

Увидеть группировку объектов в пространстве двух или трех признаков не сложно, гораздо труднее это сделать в том случае, когда признаков и групп много, а расстояния между группами невелико. Тогда на помощь исследователю приходят специальные алгоритмы обнаружения кластеров.