
- •Основы цифровой электроники
- •1.1. Логические функции
- •1.1.1Аксиомы и теоремы алгебры логики
- •1.1.2Операция сумма по модулю два
- •1.2. Логические элементы
- •Комбинационные схемы
- •1.3. Некоторые системы счисления
- •1.4. Дешифратор
- •1.5. Шифратор
- •1.6. Демультиплексор
- •1.7. Увеличение разрядности дешифраторов и демультиплексоров
- •1.8. Мультиплексор
- •1.9. Преобразователи кода
- •1.10. Сумматоры
- •Последовательностные схемы
- •1.11. Триггеры
- •1.11.1Асинхронный rs-триггер
- •1.11.2Синхронный rs-триггер
- •1.11.4Синхронный (динамический) d-триггер
- •1.11.5Универсальный jk-триггер
- •1.11.7Взаимные преобразования триггеров
- •1.12. Счетчики
- •1.13. Регистры
1.1.2Операция сумма по модулю два
Кроме основных операций алгебры логики, определяемых аксиомами (1.2)‑(1.5), целесообразно пользоваться более сложными операциями, такими как И-НЕ (1.13), ИЛИ-НЕ и сумма по модулю два.
Операция сумма по модулю два (исключающее ИЛИ, логическая неравнозначность) обозначается символом и определяется соотношением
![]() . (1.18)
. (1.18)
На основании аксиом алгебры логики можно показать, что
00=11=0, 01=10=1. (1.19)
Из данных соотношений следует, что значение ху совпадает со значением младшего разряда суммы двух двоичных чисел, где х и у – значения младших разрядов этих чисел. Соответственно этому значение i-го разряда суммы двух двоичных чисел будет определяться значением хiyizi, где хi и yi – значения i-х разрядов двоичных чисел, а zi – перенос в i-й разряд из предыдущего i–1-го разряда.
С точки зрения приоритетности выполнения операция исключающее ИЛИ занимает промежуточное положение между операциями И и ИЛИ.
1.2. Логические элементы
Физическое устройство, реализующую одну из основных операций алгебры логики, Называется логическим элементом (ЛЭ). Схема, составленная из конечного числа ЛЭ по определенным правилам, соответствующим заданной логической функции, называется логической схемой (ЛС). Построение ЛС основано на следующих правилах:
выход ЛЭ можно подсоединять ко входам нескольких ЛЭ;
на входы ЛЭ можно подавать сигналы, представляющие собой константы 0 и 1;
выходы ЛЭ нельзя соединять вместе (кроме так называемых ЛЭ с открытым коллекторным выходом);
выходы ЛЭ нельзя напрямую подключать к собственным входам.
ЛЭ может иметь любое число обратных связей, по которым выходные сигналы некоторых ЛЭ возвращаются на собственные входы, предварительно пройдя через некоторое число других ЛЭ.
Логические элементы выпускаются в виде интегральных схем. На рисунке представлены условные графические обозначения (УГО) таких элементов, выполненные в соответствии с требованиями ЕСКД:
![]() Элемент
НЕ (NOT,
Inverter).
Функция
Элемент
НЕ (NOT,
Inverter).
Функция
![]() .
.
![]() Элемент
И (AND).
Функция
Элемент
И (AND).
Функция
![]() .
.
![]() Элемент
И-НЕ (NAND).
Функция
Элемент
И-НЕ (NAND).
Функция
![]() .
.
![]() Элемент
ИЛИ (OR).
Функция
Элемент
ИЛИ (OR).
Функция
![]() .
.
![]() Элемент
ИЛИ-НЕ (NOR).
Функция
Элемент
ИЛИ-НЕ (NOR).
Функция
![]() .
.
![]() Элемент
исключающее ИЛИ (ХOR).
Функция
Элемент
исключающее ИЛИ (ХOR).
Функция
![]() .
.
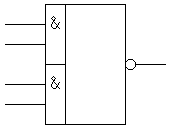 Элемент
И-ИЛИ-НЕ (AND-NOR).
Функция
Элемент
И-ИЛИ-НЕ (AND-NOR).
Функция
![]() .
.
Ряд ЛЭ может быть реализован на ЛЭ других типов. Например, ЛЭ «исключающее ИЛИ» можно реализовать на ЛЭ типа 2И-НЕ:

Действительно, логическая функция для элемента «исключающее ИЛИ» задается выражением (1.18). Приведенная схема реализует функцию
![]()
что соответствует функции «исключающее ИЛИ».
Комбинационные схемы
В комбинационных схемах логическая функция зависит только от комбинации значений входных переменных.
При описании многих цифровых устройств невозможно обойтись без упорядоченных двоичных наборов входных и выходных сигналов. Эти наборы удобно представлять в тех или иных системах счисления (СС).
1.3. Некоторые системы счисления
В позиционных СС "вес" каждого разряда зависит от его позиции в числе. К числу непозиционных относится "римская" СС, например число XVII.
Любое целое неотрицательное n-разрядное целое число в позиционной системе счисления может быть представлено в виде:
D = Cn-1*bn-1+ Cn-2*bn-2d + ... + C1*b1 + C0*b0, (2.1)
где D – десятичный эквивалент числа, С – значение i-гo разряда, b – основание системы счисления, b в степени i – вес (весовой коэффициент) i-гo разряда.
В цифровой и вычислительной технике наиболее распространены двоичная (BIN), десятичная (DEC), шестнадцатеричная (HEX) и непозиционная двоично-десятичная (BCD) системы счисления. В BCD системе вес каждого i-гo десятичного разряда равен 10 в степени i, как в десятичной системе, а каждая цифра i-гo разряда кодируется 4-мя двоичными цифрами. Восьмиричная СС (ОСТ) применяется реже. В 16-ной системе счисления цифры от 0 до 9 совпадают с десятичными, а для ЦИФР больше 9 используются буквы латинского алфавита : А(а) = цифра 10, В(b)=11, С(с)=12, D(d)=13, Е(е)=14, F(f)=15. Двоичное число преобразуется в десятичное беззнаковое число по формуле (2.1), например
10010011 = 1*27 + 1*24 + 1*21 + 1*20 = 147 (DEC).
Для перевода числа из двоичной системы в 16-ную, его необходимо разбить, начиная справа, на группы по 4 двоичных цифры и в каждой четверке просуммировать веса (8,4,2,1), соответствующие единичным значениям С. Для обратного перевода каждая HEX цифра заменяется четверкой двоичных, незначащие нули слева, если они есть, отбрасываются.
Примеры преобразований:
Найдите десятичное число без знака, соответствующее двоичному числу 00111011.
Пояснение: |
Номер разряда |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
Вес разряда |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
Значение разряда |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
ОТВЕТ: |
Десятичный эквивалент |
0 + |
0 + |
32+ |
16+ |
8 + |
0+ |
2 + |
1 = |
59(DEC) |
Найти (HEX)16-ный код приведенного выше двоичного числа 00111011.
Пояснение: |
Номер разряда |
3 |
2 |
1 |
0 |
|
3 |
2 |
1 |
0 |
|
|
|
Вес разряда |
8 |
4 |
2 |
1 |
|
8 |
4 |
2 |
1 |
|
|
|
Значение разряда |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
|
ОТВЕТ: |
16-ный эквивалент |
0 + |
0 + |
2+ |
1 |
(3) |
8 + |
0+ |
2 + |
1 = |
(11) |
3В(HEX) |
так как в HEX коде цифра 11 записывается посредством буквы В. |
||||||||||||
Двоично-десятичное число также, как и шестнадцатеричное, записывается четверками двоичных, но вес каждой четверки не 16i, а 10i. Двоично-десятичное число (BCD) можно записывать и десятичными цифрами, например 1998, и двоичными – 0001 1001 1001 1000 = 1*103 + 9*102 + 9101 + 8*100. Каждое десятичное число можно представить в виде BCD, например 19(DEC) = 19(BCD), но их двоичные представления не равны: 10011 (19DEC) не равно 1 1001(19BCD). He каждая запись из нулей и единиц является двоично-десятичным числом. Например, 11001001(BIN) = [C9(HEX), 201(DEC)] = ?9(BCD), т.к. десятичной цифры 1100=12 не существует.
