6.2. Локальная и интегральная теоремы Лапласа

Выше мы рассмотрели формулу Бернулли, которая позволяет находить вероятность появления события в испытанияхраз. Эту формулу удобно использовать в тех случаях, когда число испытанийневелико. Если же, например, надо найтиP₅₀(30), то в этом случае сталкиваемся с вычислением. Но даже не все современные калькуляторы могут вычислить это значение. При использовании стандартной записи числа приходится делать округления, отбрасывая значащие цифры, что приводит в процессе вычислений к накоплению погрешностей.

Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно kраз вnиспытаниях, если число испытаний достаточно велико.

Заметим, что для частного случая, а именно для p=1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольногоp, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь иногда называют теоремой Муавра – Лапласа.

Мы приведем только формулировку этой теоремы, опуская ее доказательство.

Теорема 6.1 (локальная теорема Лапласа).

Если вероятность pпоявления событияAв каждом испытании постоянно и отличается от нуля и единицы, то вероятностьP_n(k) того, что событиеAпоявится вnиспытаниях ровноkраз, приближенно равна (тем точнее, чем большеn):

, где. (6.2)

Функция называется малой функций Лапласа. Значения функции(x), соответствующие положительному значению аргумента, определяется из соответствующей таблицы. Для отрицательных значений аргумента пользуются той же таблицей, так как(x) четная функция, т.е. .

Вновь предположим, что производится испытаний, в каждом из которых вероятность появления событияпостоянна и равна. Как вычислить вероятностьтого, что событиепоявится вnиспытаниях не менееи не болеераз (для краткости будем говорить «отдораз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим, опустив доказательство.

Теорема 6.2 (интегральная теорема Лапласа).

Если вероятность появления событияв каждом испытании постоянно и отличается от нуля и единицы, то вероятностьтого, что событиепоявится вnиспытаниях отдораз, приближенно равна:

, где. (6.3)

Функция 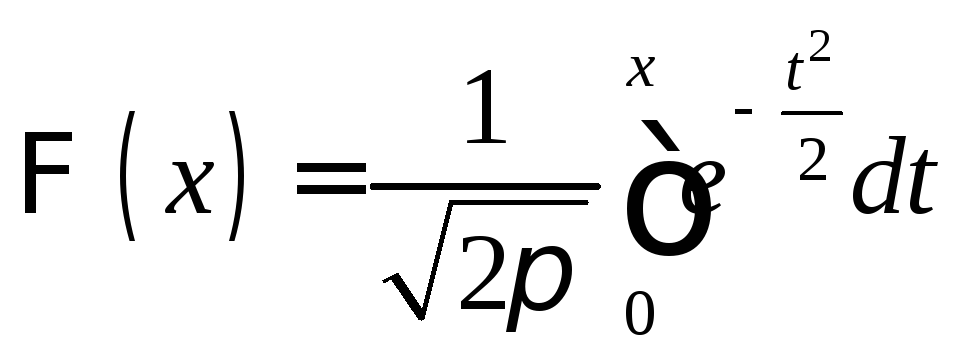называется функций Лапласа. Значения функции(x), соответствующие положительному значению аргументаи, определяется из соответствующей таблицы. Для отрицательных значений аргумента можно пользоваться той же таблицей, так как(x) нечетная функция, т.е.. В таблице приводятся значения лишь до. Приможно принять.

Замечание. Локальной и интегральной теоремами Лапласа на практике удобно пользоваться в случае, если npq>10. Если же npq<10, то эти формулы приводят к большим погрешностям.

Пример 6.4.Вероятность появления событияAв каждом из 900 независимых испытаний равнаp=0,8. Найти вероятность того, что событиеAпроизойдет:

а) 750 раз;

б) не менее 710 раз и не более 740 раз.

Решение.а) Из условия следует, чтоn=900,k=750,p=0,8, поэтомуq=0,2. Посколькуnpq=9000,80,2=144>10, то можно воспользоваться локальной теоремой Лапласа.

Находим x:

.

По таблице значений функции находим (2,5)=0,0175.

Согласно локальной теореме Лапласа получаем искомую вероятность:

.

б) Из условия следует, что n=900,k₁=710,k₂=740,p=0,8, поэтомуq=0,2. Находимx₁иx₂:

;

.

По таблице значений функции Лапласа, учитывая нечетность функции, определяем

(x₁)=(0,83)=0,2967;

(x₂)=(1,67)=0,4525.

Согласно интегральной теореме Лапласа получаем искомую вероятность:

. 