4. Теоремы сложения и умножения

ВЕРОЯТНОСТЕЙ

4.1. Теорема сложения вероятностей

Теорема 4.1.Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

. (4.1)

Следствие.Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

.

Теорема 4.2.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

. (4.2)

Теорема 4.3.Сумма вероятностей противоположных событий равна единице:

. (4.3)

Пример 4.1.На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы два учебника окажется в переплете;

Решение.1) ПустьA– событие, заключающееся в том, что хотя бы два учебника из трех отобранных будет в переплете. СобытиеAбудет состоять из двух несовместных событий:A₁– событие, состоящее в том, что из трех отобранных учебников два в переплете, а один – нет;A₂– событие, состоящее в том, что из трех отобранных учебников все три в переплете. Тогда.

Поскольку события A₁иA₂несовместны, то по теореме 4.1. получаем

.

Вероятности событий A₁иA₁находим, используя классическое определение вероятностей.

.



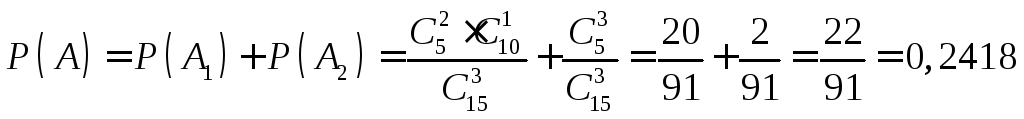4.2. Теорема умножение вероятностей

Пусть при выполнении некоторого комплекса условий могут произойти случайные события AиB. Их вероятность соответственно обозначим черезP(A) иP(B). Допустим, что стало известно о наступлении событияA, а относительно событияBданных не получено. Таким образом, комплекс условий для наступления событияBизменился, вероятность наступления событияBможет стать другой, отличной отP(B). Если, например, при бросании игральной кости вероятность выпадения единицы равна 1/6, то после того, как стало известно, что выпало нечетное число очков, эта вероятность стала равна 1/3.

Событие, состоящее в том, что случится событие B, когда известно, что произошло событиеA, будем обозначать символомB/A. Соответствующая вероятностьP(B/A) называетсяусловной вероятностьюсобытияBпри условии, что событиеAпроизошло.

В следующей теореме мы введем формулу для вычисления условной вероятности. Теорему примем без доказательства.

Теорема 4.4.

. (4.4)

Аналогично

. (4.5)

Теорема 4.5(теорема умножения вероятностей).

Вероятность совместного наступления двух событий (вероятность произведения двух событий) равна произведению вероятности одного из них на условную вероятность другого при условии, что первое уже произошло:

. (4.6)

Пример 4.2.Из урны, в которойmчерных иnбелых шаров, извлекают два шара. Чему равна вероятность того, что:

а) оба шара белых;

б) шары разного цвета.

Решение.а) ПустьA₁– событие, состоящее в том, что первый шар белый,A₂– событие, состоящее в том, что второй шар белый. Тогда

.

б) Пусть A₁B₂– событие, состоящее в том, что первый шар белый, а второй – черный,B₁A₂– событие, состоящее в том, первый шар черный, а второй – белый. Тогда



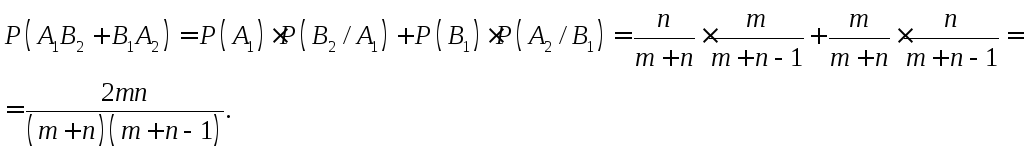
Теорему умножения вероятностей легко распространить на случай, когда событий больше двух.

Следствие.Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

,

где – вероятность событияA_n, вычисленная в предположении, что событияA₁,A₂, …,A_n-1наступили.

В частности для трех событий будем иметь: .

Заметим, что порядок, в котором расположены события, может быть выбран любым. Безразлично, какое событие считать первым, вторым и т.д.

Определение 4.1.Два события называютсянезависимыми, если вероятность одного из них не зависит от появления или не появления другого, т.е.

или.

Два события называются зависимыми, если вероятность появления одного из них зависит от наступления или не наступления другого события.

Теорема умножения вероятностей, которая была доказана выше, рассматривалась для зависимых событий. Сформулируем теорему умножения вероятностей (без доказательства) для независимых событий.

Теорема 4.6.Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

. (4.7)

Пример 4.3.Студент может уехать в университет или автобусом, который ходит через каждые 20 мин, или маршрутным такси, которое ходит через каждые 10 мин. Какова вероятность того, что студент, подошедший к остановке, уедет в течение ближайших пяти минут?

Решение.ПустьA– событие, заключающееся в том, что студент, подошедший к остановке, уедет в течение ближайших пяти минут. СобытиеAбудет состоять из двух совместных событий:A₁– событие, состоящее в том, что студент в течение пяти минут уедет автобусом;A₂– событие, состоящее в том, что студент в течение пяти минут уедет маршрутным такси. Совместность этих событий заключается в том, что к остановке одновременно может подойти как автобус, так и маршрутное такси. Но эти события независимые. Поэтому по т.4.2. и по т.4.6. имеем

.



Пусть в результате испытания может появиться nсобытий независимых в совокупности, либо некоторые их них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема 4.7.Вероятность появления хотя бы одного из событийA₁,A₂, …,A_n, независящих в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:

. (4.8)

Пример 4.4(Условие примера4.1.). На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете;

Решение.1) ПустьA– событие, заключающееся в том, что хотя бы один из трех отобранных учебников будет в переплете. Рассмотрим противоположное событие- состоящее в том, что ни один из трех взятых учебников не будет в переплете. СобытияAиобразуют полную группу событий. Значит,. Тогда

.



Пример 4.5.Вероятности попадания в цель при стрельбе из трех орудий таковы:p₁=0,8,p₂=0,7,p₃=0,9. Найти вероятность:

а) только одного попадания при одном залпе из всех орудий;

б) хотя бы одного попадания при одном залпе из всех орудий.

Решение.а) ПустьA– событие, состоящее в том, что при одном залпе из всех орудий было только одно попадание. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий. СобытиеAвозможно при появлении одного из попарно несовместных событийA₁, илиA₂, илиA₃.

A₁– событие, состоящее в том, что произошло попадание в цель первым орудием, т.е. первое орудие попало, второе и третье – нет, значит,

;

A₂– событие, состоящее в том, что произошло попадание в цель вторым орудием, т.е. второе орудие попало, а первое и третье – нет,

;

A₃– событие, состоящее в том, что произошло попадание в цель третьим орудием, т.е. третье орудие попало, а первое и второе – нет,

.

Таким образом, получаем .

События B₁,B₂,B₃независимы. Используя теоремы сложения и умножения вероятностей, получаем:

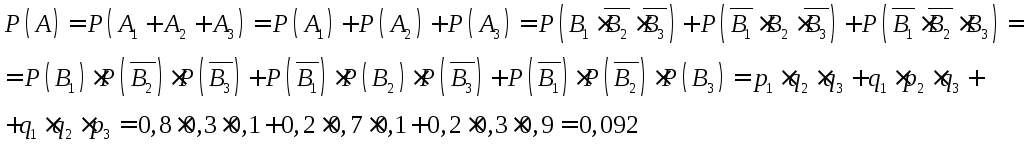гдеq₁,q₂,q₃– соответствующие вероятности промаха каждым орудием.

б) Пусть C– событие, состоящее в том, что при одном залпе из всех орудий было хотя бы одно попадание. Рассмотри противоположное событие, состоящее в том, что при одном залпе не было ни одного попадания, т.е.. СобытияCиобразуют полную группу, поэтому сумма их вероятностей равна единице. Следовательно, получаем

.



Теоремы сложения и умножения вероятностей широко используются при расчете вероятности безотказной работы или вероятности разрыва электрической цепи, если даны, например, вероятности отказа каждого узла, входящего в электрическую схему. Как известно, соединения приборов в электрической цепи возможно двумя способами: параллельномилипоследовательном.

Пусть два прибора Z₁иZ₂соединены последовательно. Вероятность отказа каждого прибора соответственно равноp₁иp₂. Поставим вопрос: какова вероятность того, что электрическая схема выйдет из строя? Какова вероятность того, что электрическая схема будет работать некоторое время безотказно?

Вероятности безотказной работы каждого прибора в течение некоторого времени будут равны .

Пусть A– событие, состоящее в том, что схема выйдет из строя,- событие, состоящее в том, что схема будет работать безотказно. Тогда

Пусть два прибора Z₁иZ₂соединены параллельно. Вероятность отказа каждого прибора соответственно равноp₁иp₂. Поставим вопрос: какова вероятность того, что электрическая схема выйдет из строя? Какова вероятность того, что электрическая схема будет работать некоторое время безотказно?

Вероятности безотказной работы каждого прибора в течение некоторого времени будут равны .

Пусть A– событие, состоящее в том, что схема выйдет из строя,- событие, состоящее в том, что схема будет работать безотказно. Тогда

Пример 4.6.Дана электрическая схема, в которой вероятность отказов узлов, за времяTравнаp₁=0,2;p₂=0,1;p₃=0,2;p₄=0,4. Схема выходит из строя, если цепь разомкнута. Определить вероятность того, что цепь не пропустит электрический ток.

Решение.Пустьсобытие, заключающееся в том, что в цепи тока нет. Цепь разобьем на два участка:и, которые соединены последовательно.

, гдеивероятность того, что ток есть.

Тогда

.

Участок разбиваем на два участка:и, которые соединены параллельно. Пустьсобытие, заключающееся в том, что на этом участке ток есть. Тогда

,

где вероятность того, что на участкетока нет,вероятность того, что на участкетока нет.

По условию p₁=0,2. Участокесть последовательное соединение двух элементови. Тогда

.

Далее

.

Следовательно,

.

