3.2.4. Дифференцирование обратной функции

Теорема 3.6 (о производной обратной функции). Пусть функция непрерывна и строго возрастает (убывает) в некоторой окрестности точки , дифференцируема в точке и производная в этой точке отлична от нуля: . Тогда существует обратная функция , которая в некоторой окрестности точки непрерывна и строго возрастает (убывает), дифференцируема в точке и имеет в этой точке производную, равную обратной величине производной данной функции:

, или кратко (3.9)

Пример 3.12. Найти производную функции , используя теорему 3.6 о производной обратной функции.

□ Функции и являются взаимно обратными, при этом Перепишем формулу (3.9) в виде Откуда при получим: .■

3.2.5. Логарифмическое дифференцирование. Темп роста и эластичность функции

Рассмотрим функцию принимающую положительное значение в точке и дифференцируемую в этой точке. Логарифмической производной функции в точке называют производную натурального логарифма этой функции, которую вычисляют по правилу дифференцирования сложной функции:

.

Отсюда следует, что связь между производной функции и ее логарифмической производной выражается формулой:

(3.10)

Использование логарифмической производной упрощает процесс дифференцирования следующих функций:

а) сложно-степенной функции ,

б) громоздкого произведения

в) громоздкого частного

Алгоритм применения логарифмической производной

1. Найти натуральный логарифм заданной положительной функции и упростить его при помощи свойств логарифма.

2. Найти логарифмическую производную .

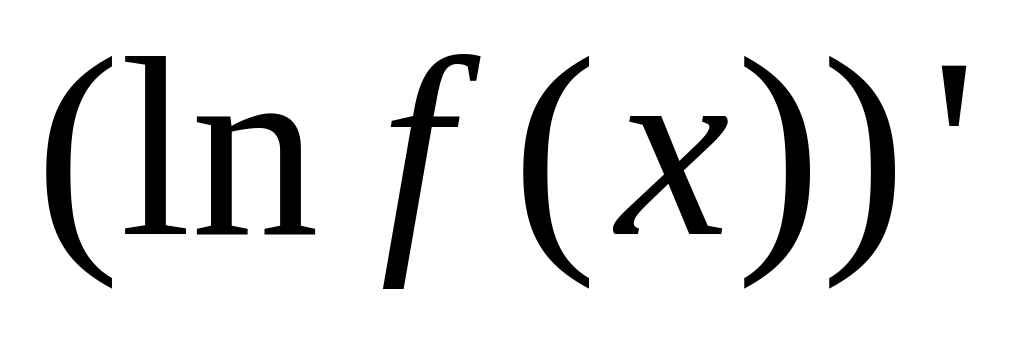3. Найти производную по формуле (3.10).

Пример 3.13. Найти производную функции

□ Функция является сложно-степенной. Она определена и принимает положительные значения при любых значениях Согласно рекомендации производную ищем с использованием логарифмической производной.

1. Логарифмируем функцию: . Упрощаем правую часть:

2. Дифференцируем обе части полученного логаифмического равенства по переменной , при этом используем правило дифференцирования сложной функции и таблицу производных:

3. Находим производную ■

В экономической теории [21, 47] логарифмическая производная используется при вычислении темпа роста и эластичности функции .

Темп роста функции равен

(3.11)

Используя логарифмическую производную, формулу (3.11) можно переписать так:

(3.12)

Эластичность функции в точке равна:

где − относительное изменение функции при абсолютном изменении

аргумента , равном − относительное изменение аргумента в точке . Из определения следует, что эластичность приближенно равна процентному изменению функции в точке при процентном изменении аргумента в этой точке на 1%.

При произвольном значении х формуле для вычисления можно придать вид:

, или (3.13)

Связь темпа роста функции с эластичностью выражается соотношением:

При анализе функции с использованием эластичности применяют следующую классификацию типов эластичности [Кремер]:

при функцию называют эластичной по

при эластичность функции называют единичной,

при функцию называют неэластичной по

при говорят, что возникает кризисная ситуация в экономике.

Пример 3.14. Найти темп роста объема выпуска для производственной функции при

□ Воспользуемся формулой (3.12):

1. Упростим выражение в скобке:

2. Найдем темп роста как производную полученного выражения:

3. Вычислим значение при ■

Пример 3.15. Найти эластичность функции спроса, заданной соотношением , в точке Указать тип эластичности в этой точке.

□ Выразим через Тогда при имеем Используем формулу (3.13) и получим:

При Спрос − эластичный, так как . ■