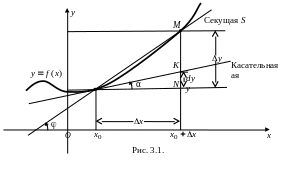
3.1.2. Смысл производной и дифференциала

Геометрический смысл производной и дифференциала

Конечная производная. Рассмотрим функцию , непрерывную в некоторой окрестности точки и имеющую конечную производную в этой точке. Возьмем на графике функции две точки: и и проведем через них прямую – секущую графика функции.

Эта прямая образует некоторый угол с положительным направлением оси Проведем через точку прямую, параллельную оси Точку пересечения этой прямой с вертикалью обозначим Угол между секущей и осью равен углу Очевидно, что для рассматриваемой возрастающей функции приращение функции равно длине отрезка а приращение аргумента – длине отрезка

При точка перемещается вдоль заданной кривой и неограниченно приближается к точке При этом секущая поворачивается вокруг точки и стремится к предельному положению, называемому касательной к кривой в точке Эта прямая образует угол с положительным направлением оси абсцисс.

Угловой коэффициент секущей равен тангенсу угла где Угловой коэффициент касательной получим при помощи предельного перехода по формуле:

(3.6)

Отсюда следует геометрический смысл производной: значение производной равно угловому коэффициенту касательной.

Касательная пересекает вертикаль в точке Абсцисса этой точки равна ордината , где Так как производная конечна, то и угловой коэффициент конечен и . Отсюда следует геометрический смысл дифференциала: значение дифференциала функции в точке , соответствующего приращению аргумента равно приращению ординаты касательной, проведенной к графику функции в точке

Е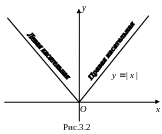 сли функция непрерывна в точке , не дифференцируема в этой точке, но имеет неравные конечные односторонние производные в этой точке, то через точку можно провести две односторонних касательных с угловыми коэффициентами, равными . Односторонние (левосторонняя и правосторонняя) касательные изображаются полупрямыми, ведущими с той или иной стороны (левой или правой) к точке и имеющими указанные угловые коэффициенты.

У функции в точке нет производной, но существуют односторонние производные Ветви графика являются одновременно односторонними касательными к графику в начале координат (см. рис. 3.2).

П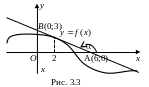 ример 3.6. Найти значение производной функции если касательная, проведенная к графику функции в точке , пересекает координатные оси в точках (см. рис. 3.3).

□ Значение равно угловому коэффициенту касательной. Касательная − прямая линия, проходящая через точки . По формуле (1.8) угловой коэффициент прямой, проходящей через две заданные точки , равен ■

Бесконечная производная. Рассмотрим функцию , непрерывную на отрезке и имеющую бесконечные производные в точках . В этом случае вертикальные прямые, уравнения которых , являются касательными к графику функции в точках

На рис. 3.4 приведены вертикальные касательные в этих точках, соответствующие следующим сочетаниям значений односторонних производных:

а) б) в)

г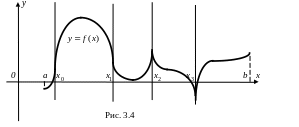 ) Подчеркнем, что во всех четырех случаях .

В примерах 3.4 и 3.5 рассмотрены функции с бесконечными производными в точке В обоих случаях через одну и ту же точку проходит вертикальная касательная, совпадаюшая с осью ординат. Принципиальное различие состоит в том, что одна функция − − непрерывна в точке , а другая − − терпит разрыв 1-го рода в точке . На рис. 3.5 приведены графики обеих функций вместе с касательными, проходящими через точку

Т аким образом, непрерывность функции в точке является необходимым условием существования только конечной производной. В случае бесконечной производной функция может быть как непрерывной, так и разрывной в соответствующей точке.

Механический смысл производной и дифференциала

Пусть − время, − путь, пройденный материальной точкой при прямолинейном движении за время . Среднюю скорость движения на временном отрезке определяют так: где Скорость (мгновенную скорость) движения в момент времени определяют при помощи операции предельного перехода: Значит, скорость движения равна производной от пройденного пути по времени t.

Дифференциал равен пути, пройденному с момента по момент времени , при движении с постоянной скоростью, равной

Пусть − независимая переменная, − некоторая функция, определенная на промежутке . По аналогии с задачей о движении точки средней скоростью изменения функции на отрезке назовем . Тогда скорость изменения функции в точке определяется при помощи операции предельного перехода и равна значению производной функции в точке : .

В механике при изучении прямолинейного движения точки наряду со скоростью используют понятие ускорения , которое определяют как скорость изменения скорости движения, т.е.

Пример 3.5. Найти скорость прямолинейного движения точки, если зависимость пройденного пути от времени имеет вид: , при

□ Искомая скорость равна значению производной Производная Эту соотношение можно вывести, используя определение производной или применяя правила дифференцирования, изложенные далее. Тогда ■

Экономический смысл производной и дифференциала

В экономике производные применяют для получения предельных издержек производства или хранения, предельной выручки от продаж, предельной прибыли и т.п.

Если функция есть функция издержек (затрат) при производстве количества однородной продукции, то называют средним приращением издержек производства. Значение равно приращению издержек производства на единицу приращения количества продукции.

Производную называют предельными издержками производства.

Аналогично, если выручка от продажи единиц товара, то производную называют предельной выручкой.

Если функция описывает зависимость цены некоторого товара (продукта) от времени , то производная равна скорости изменения цены в выбранный момент времени и ее называют тенденцией формирования цены товара.

Дифференциал функции издержек вычисляется по формуле: . При получаем и по формуле (3.4) для приближенного вычисления приращения функции имеем . Величине производной можно дать следующий экономический смысл: если произведено изделий, то дополнительные издержки по производству -го изделия приближенно равны предельным издержкам [21].

Пример 3.6. Издержки производства зависят от объема продукции по формуле Определить предельные издержки, если объем продукции составляет 5 единиц. Найти дополнительные издержки по производству шестого изделия.

□ Имеем При Дополнительные издержки по производству шестого изделия приближенно равны ■