3.4.3. Формулы Маклорена для некоторых элементарных функций

Формула Маклорена для функции, раз дифференцируемой в окрестности точки , имеет вид:

(3.24)

где

Ниже приведены формулы Маклорена для некоторых элементарных функций:

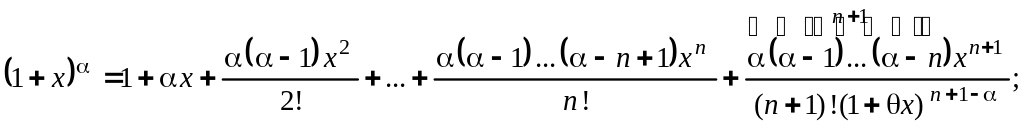
Разложение функции по формуле Тейлора (Маклорена) можно осуществлять разными способами. Учитывая единственность разложения, целесообразно сочетать разные приемы:

1. использование основных разложений по степеням x функций ;

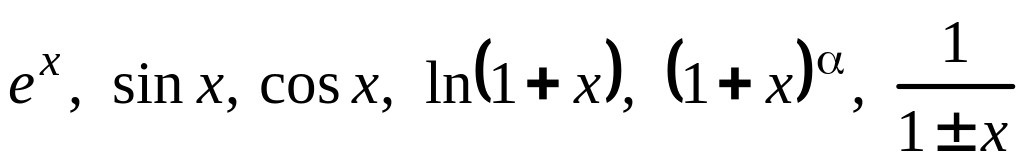2. замену переменной;

3. арифметические операции над формулами Тейлора для отдельных компонент заданной функции;

4. почленное дифференцирование и интегрирование формул Тейлора.

Пример 3.23. Разложить функцию по степеням включительно.

□ Заданная функция удовлетворяет условиям теоремы Тейлора на промежутке разложение единственно и значения коэффициентов не зависят от способа их нахождения. Решим пример двумя способами: сначала непосредственно по формулам (3.22), (3.23), затем используем сочетание разных приемов.

1. Первый способ. Общий вид разложения: Найдем все производные функции до четвертого порядка включительно:

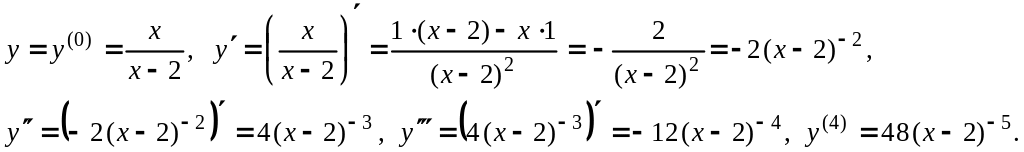
Вычислим коэффициенты по формулам (3.23) и найдем остаточный член в форме Лагранжа:

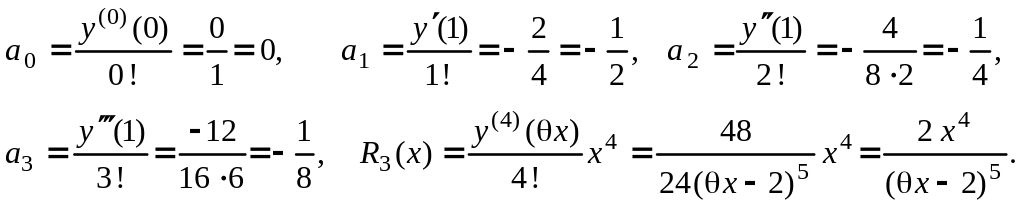
Подставим найденные коэффициенты в разложение (3.22) и получим

Если запишем остаточный член в форме Пеано: то разложение примет вид:

2. Второй способ. Перепишем функцию в виде произведения:

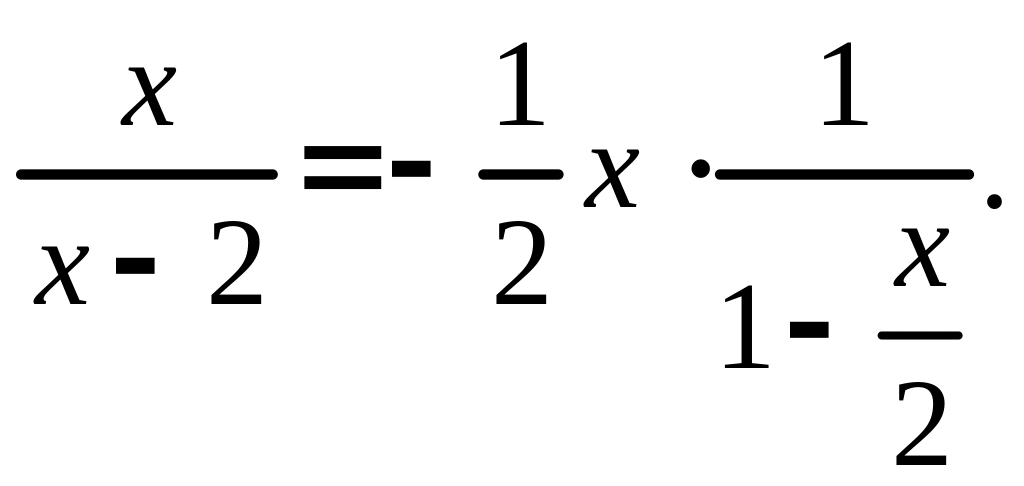
Правый множитель разложим по степеням , используя формулу Маклорена 2-го порядка для функции в сочетании с заменой переменной, взяв вместо :

=

Тогда

В ходе разложения были использованы такие свойства бесконечно малых 1) 2) , которые легко проверить, используя определение. Как видим, получено одно и тоже разложение. ■

Задачи для самостоятельного решения

1.Запишите многочлен в виде многочлена по степеням

1) 2) 3) 4)

Ответы: 1) 2) 3) 4) .

2. Разложите функцию по степеням включительно:

1) 2) 3) 4)

Ответы: 1) 2)

3) 4) .

3.5. Приложения дифференциального исчисления

3.5.1 Приближенные вычисления значений функции

В практических задачах часто возникает необходимость вычисления приближенного значения функции в некоторой точке Абсолютной погрешностью называют абсолютную величину разности между точным и приближенным значением функции в точке Величина погрешности определяет точность вычислений: чем меньше погрешность, тем точнее вычислено значение функции. Рассмотрим некоторые алгоритмы, которые позволяют найти приближенное значении функции, и сопоставим их.

Использование первого дифференциала

При вычислении приближенного значения дифференцируемой функции применима формула (3.4): которой можно придать вид:

(3. 26)

Эта формула проста в применении, но обладает существенным недостатком − нельзя заранее оценить погрешность вычислений.

Использование формулы конечных приращений

Формула конечных приращений (3.21) может быть переписана в виде:

где (3.27)

При малых приращениях аргумента полагают при этом абсолютная погрешность