Асимптоты графика функции
Асимптотой графика функции
называют такую линию на плоскости, что
расстояние от точки
до этой линии стремится к нулю при
неограниченном удалении точки графика
от начала координат.
Ограничимся рассмотрением прямых линий в качестве асимптот. График функции может иметь вертикальные, горизонтальные и наклонные асимптоты.
Вертикальная прямая
называется вертикальной асимптотой
графика функции
,
если хотя бы один односторонний предел
при
равен бесконечности:
или
Существование вертикальной асимптоты
графика функции
означает, что при
(или при
)
функция стремится к бесконечности
монотонно, если в соответствующей
односторонней окрестности точки
производная функции не меняет знак.
Говорят, что график функции неограниченно
приближается к вертикальной прямой
.
Вертикальные асимптоты проходят через точки разрыва второго рода или граничные точки области определения, в которых хотя бы односторонний предел при равен бесконечности.
Если функция
определена для всех
и существует конечный предел
то
горизонтальная прямая
называется горизонтальной асимптотой
при
,
или правосторонней (правой) горизонтальной
асимптотой. Аналогично определяется
горизонтальная асимптота при
.
Существование горизонтальной асимптоты
означает, что при
(или при
)
функция
ведет себя «почти как» постоянная
с точностью до бесконечно малой.
Если функция
определена для всех
и представима в виде
при
,
где слагаемое
является бесконечно малой величиной
высшего порядка малости относительно
,
то наклонная прямая
называется
наклонной асимптотой при
,
или правосторонней (правой)
наклонной асимптотой. Аналогично
определяют наклонную асимптоту при
.
Если существует наклонная асимптота
при
(или при
),
то график функции при
(или
при
)
ведет себя «почти как» наклонная прямая
с точностью до бесконечно малой.
Теорема 3.22. Пусть функция
определена для всех
.
Чтобы прямая
была наклонной асимптотой графика
функции при
необходимо и достаточно, чтобы существовали
конечные пределы:
и
Аналогично
находят наклонную асимптоту при
Пример
3.44. Найти асимптоты графика функции
□ Функция
определена
и непрерывна на всей числовой оси,
следовательно, не имеет точек разрыва
и поэтому у нее нет вертикальных асимптот.
Н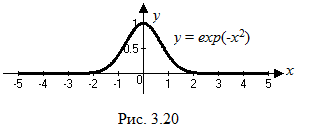
айдем
предел:
Отсюда следует, что
является правой горизонтальной асимптотой
заданной кривой. С учетом четности
функции
ясно,
что ось абсцисс является одновременно
и левосторонней, и правосторонней
горизонтальной асимптотой. При больших
по абсолютной величине значениях
график функции слабо отклоняется от
оси абсцисс (см. рис.3.20). ■
Пример 3.45. Найти асимптоты графика
функции
□
Функция
определена и непрерывна при
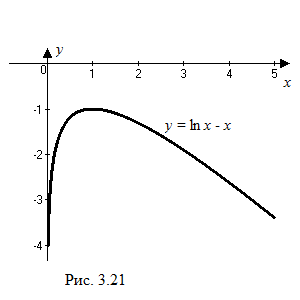
График функции имеет вертикальную
асимптоту
,
проходящую через граничную точку области
определения
,
так как
(см. рис. 3.21).
График не имеет правосторонней
горизонтальной асимптоты, так как
(см. пример 3.32).
Чтобы выяснить, имеет ли график правостороннюю наклонную асимптоту, вычислим пределы:
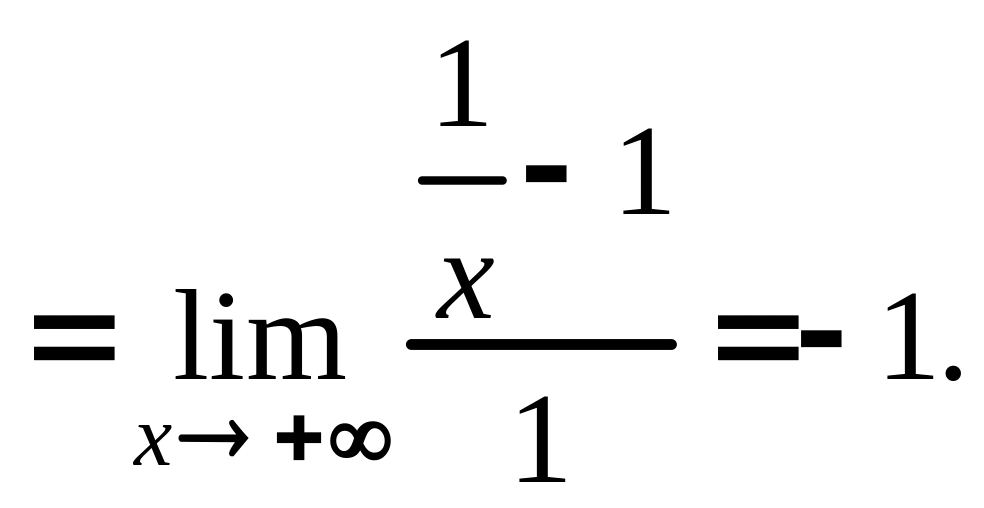
Второй предел не является конечным.
Вывод: нет наклонной асимптоты.■
Пример 3.46. Найти асимптоты графика
функции
□ Функция
определена и непрерывна при
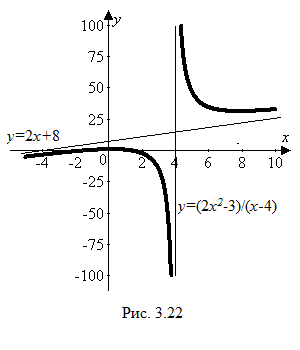
Точка
является точкой разрыва 2-го рода:
.
Следовательно,
− вертикальная асимптота (см. рис. 3.22).
График
не имеет горизонтальных асимптот, так
как
При вычислении предела использовано второе правило Лопиталя.
Наклонная асимптота
существует и является одновременно и
левосторонней, и правосторонней
асимптотой.
Действительно,
■