3.6.4. Общая схема исследования функции и построения графика

Пусть задана функция Исследование свойств функции и построение графика функции целесообразно проводить в следующей последовательности, называемой общей схемой исследования функции:

1. найти область определения функции ;

2. найти точки пересечения графика с координатными осями и промежутки знакопостоянства функции;

3. исследовать функцию на четность-нечетность и периодичность;

4. исследовать функцию на непрерывность, найти точки разрыва и вертикальные асимптоты;

5. исследовать поведение функции на бесконечности, найти горизонтальные и наклонные асимптоты;

6. найти промежутки монотонности и точки экстремума;

7. найти промежутки выпуклости и точки перегиба;

8. составить таблицу значений функции и ее первых двух производных;

9. построить график.

Под построением графика понимается построение эскиза графика функции, который в полной мере отражает свойства функции, полученные в ходе ее исследования.

Пример 3.47. Исследовать функцию: .

□ 1) Область определения:

2. Точки пересечения с осью

или точка .

Точки пересечения с осью

Исследуем знак

–

+

–

+

−1

0

1

2. Область симметрична, исследуем на четность и нечетность.

т. е. − нечетная функция, следовательно, ее график имеет симметрию относительно начала координат и достаточно выполнить исследование функции при

Периодичность: при не является периодической.

2. Функция является элементарной функцией. Поэтому область определения

одновременно является областью непрерывности. Точки являются точками разрыва , так как в них не определена. Вычислим в этих точках односторонние пределы:

точки являются точками разрыва второго рода, а прямые являются для графика вертикальными асимптотами.

5) Найдем предельные значения функции на границах области определения: ;

аналогично Отсюда следует, что у графика нет горизонтальных асимптот.

В силу нечетности функции ограничимся поиском асимптоты при Наклонную асимптоту ищем в виде

,

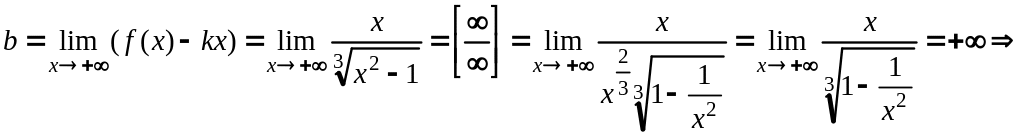нет правой асимптоты. Вместе с ней нет и левой наклонной асимптоты.

6) =

;

; изучим знак

max

min

В

­−1

1

ывод: максимум в точке , так как знак первой производной меняется с положительного на отрицательный, минимум в точке , так как знак первой производной меняется с отрицательного на положительный. Соответствующие значения функции: .

7) .

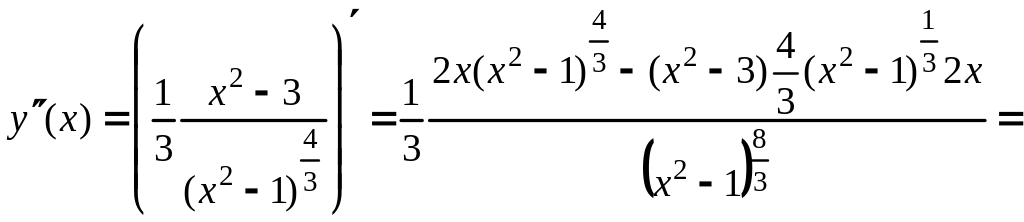
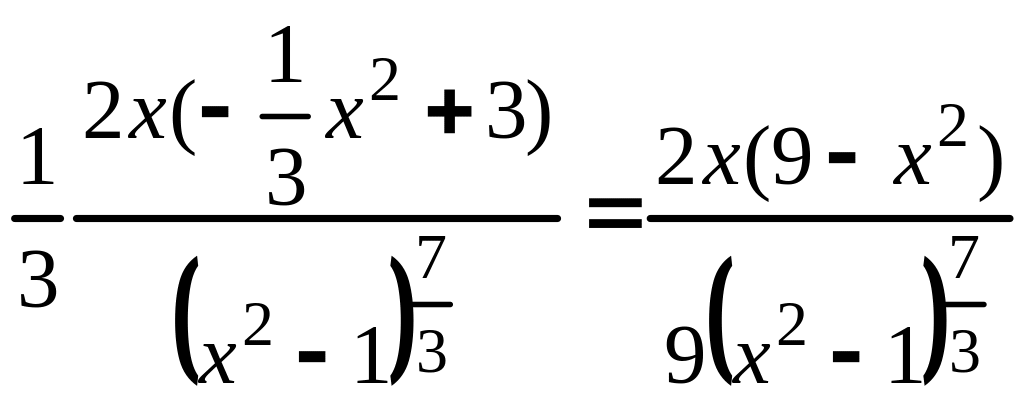Исследуем знак где

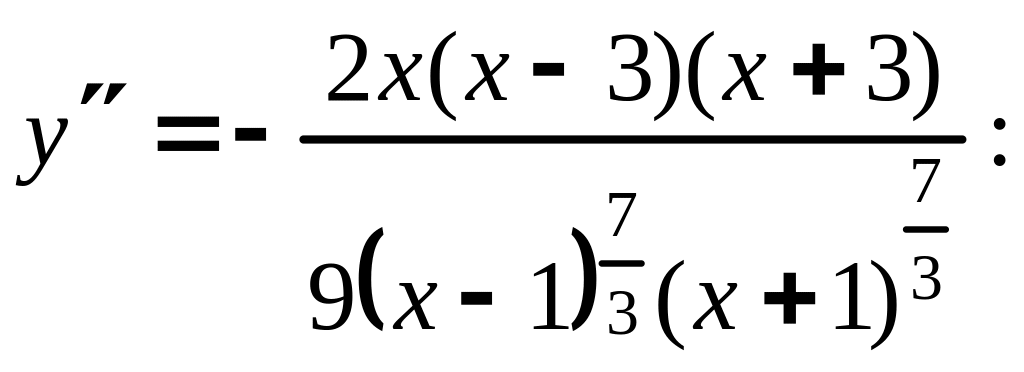
-1

0

1

3

-3

-1

0

1

т.п.

т.п.

т.п.

−3

−1

0

1

3

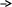
Точки являются точками перегиба, поскольку знаки второй производной слева и справа от них различны; точки поэтому не могут быть точками перегиба. Найдем точки перегиба графика функции, соответствующие точкам перегиба:

точка перегиба графика

точка перегиба графика точка перегиба графика

8) Для данной функции таблицу достаточно сделать только для , так как нечетная. Для функции общего вида таблица делается на всей области определения. В заголовок таблицы заносятся все характерные точки функции точки разрыва, критические точки 1-го и 2-го рода и промежутки между ними.

Табл. 3.4

			1				3
	−	−		−	0	+	+	+
	0	−		+	+	+	0	−
	т. п. 0				min		т. п. 1,5

Г

рафик функции изображен на рис. 3.23. Очевидно, что множество значений ■

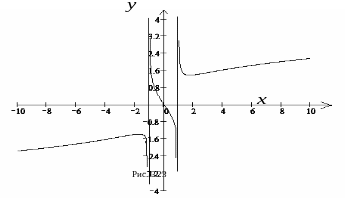
З а м е ч а н и е. При построении графика следует учитывать, что если в точке экстремума то касательная к графику параллельна оси Оx, а если то касательная к графику параллельна оси Oy (вертикальная прямая).

Пример 3.48. Исследовать функцию и построить ее график.

□ 1) Область определения

2) Точки пересечения с осью Oy: точка (0;0).

Точки пересечения с осью Ox: так как точка (0;0).

И

0 x

сследуем знак учитывая, что при любых

3) Область определения симметрична, вычислим . т. е. − функция общего вида.

Периодичность: при , т.е. функция не периодическая.

4) определена и непрерывна на нет вертикальных асимптот.

2. Исследуем поведение функции при и при

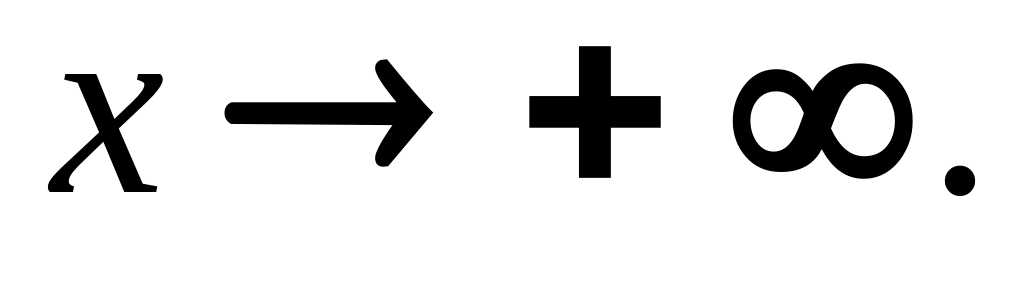
нет левой горизонтальной асимптоты.

Попробуем найти левую наклонную асимптоту в виде . Ищем угловой коэффициент k: нет левой наклонной асимптоты.

Здесь при вычислении предела применено правило Лопиталя. Отсюда следует, что − правая горизонтальная асимптота.

6) Исследуем функцию при помощи первой производной:

И

сследуем знак

1

max

1

х

точка − точка максимума, так как производная меняет знак с положительного на отрицательный.

7) Исследуем функцию при помощи второй производной:

Исследуем знак

точка − точка перегиба, так как знаки второй производной слева и справа от нее различны.

8) Заполним таблицу.

Таблица 3.5

		1		2
	+	0	−	−	−
	−	−	−	0	+
				т. п.

График функции изображен на рис. 3.24. Очевидно, что область значений .

З

-1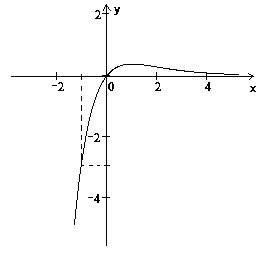

аметим, что при построении графика взята еще одна точка:

■

Рис. 3.24