3.6.2. Промежутки выпуклости вверх и вниз и точки перегиба

Рассмотрим функцию, дифференцируемую на некотором промежутке. Функцию называют выпуклой вниз (вверх) на этом промежутке, если ее график расположен не ниже (не выше) касательной, проведенной в произвольной точке этого промежутка. Соответственно график называют выпуклым вниз (вверх) на этом промежутке.

На рис. 3.16 приведен график функции , выпуклой вниз на промежутках и выпуклой вверх на промежутках

Согласно определению, о направлении выпуклости судят по расположению графика относительно касательной. На рис. 3.16 нанесены касательные, проведенные в точках с абсциссами меньшими Как видно, график функции лежит под обеими касательными и на промежутке является выпуклым вверх. Аналогичным способом можно обосновать наличие остальных промежутков выпуклости вверх или вниз.

Точкой перегиба функции называют точку , принадлежащую области определения, при переходе через которую меняется направление выпуклости функции. Соответствующую точку графика функции называют точкой перегиба графика функции. В точке перегиба графика изменяется направление выпуклости: при переходе подвижной точки вдоль кривой, описываемой функцией, график из выпуклого вниз становится выпуклым вверх, и наоборот. Говорят, что в точке перегиба график переходит с одной стороной касательной на другую.

Для функции , приведенной на рис. 3.16, точки являются точками перегиба функции, так как при переходе через эти точки меняется направление выпуклости. При переходе через точку также меняется направление выпуклости, но эта точка не принадлежит области определения, и поэтому не является точкой перегиба.

Чтобы найти промежутки выпуклости и точки перегиба, используют теоремы, приведенные ниже.

Теорема 3.19 (достаточное условие выпуклости функции на промежутке). Если вторая производная функции положительна (отрицательна) на некотором промежутке, то функция выпукла вниз (вверх) на этом промежутке.

В частности, если в каждой точке некоторого интервала , то выпукла вниз на этом интервале. Если то выпукла вверх на этом интервале.

Сформулированное правило можно назвать правилом «улыбки», ассоциируя знак «+» второй производной с хорошим настроением и улыбкой ( ), а знак «−» с плохим настроением и грустной гримасой ( ).

Теорема 3.20 (необходимое условие перегиба). Если − точка перегиба функции , то вторая производная в точке перегиба равна нулю или конечная вторая производная не существует:

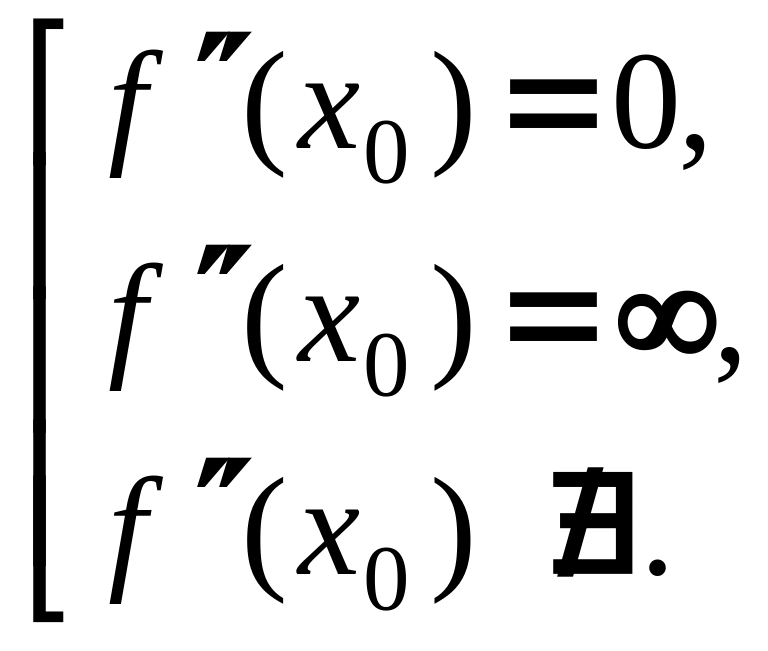(3.37)

Точки, принадлежащие области определения функции и удовлетворяющие совокупности (3.37), называют критическими точками второго рода функции (критическими точками функции по второй производной). В этих точках возможен перегиб графика. Среди критических точек 2-го рода нужно делать отбор при помощи достаточных условий перегиба.

Теорема 3.21 (достаточное условие перегиба). Если вторая производная меняет знак при переходе через критическую точку 2-го рода функции , то эта точка является точкой перегиба функции.

Заметим, что есть еще одно правило выделения точек перегиба из множества критических точек 2-го рода. Оно сформулировано в теореме 3.18. Из этой теоремы следует, что если стационарная точка функции не является точкой экстремума, то эта точка есть точка перегиба.

Алгоритм исследования функции на выпуклость

и точки перегиба

1. Найти область определения функции .

2. Найти вторую производную .

3. Найти критические точки 2-го рода из условий 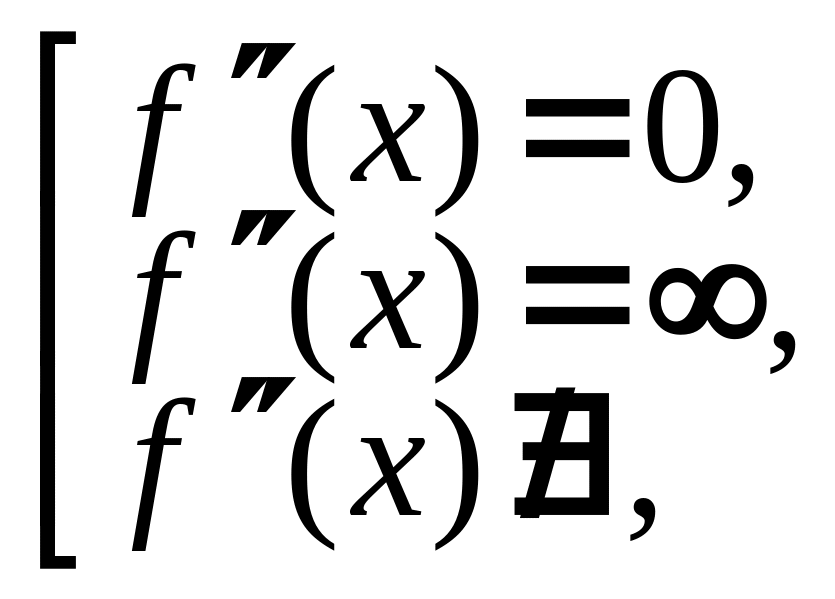и .

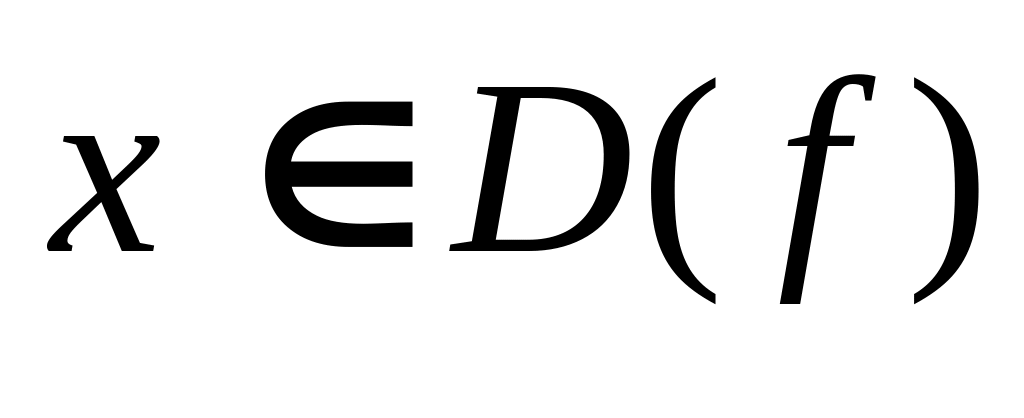4. Исследовать знак второй производной 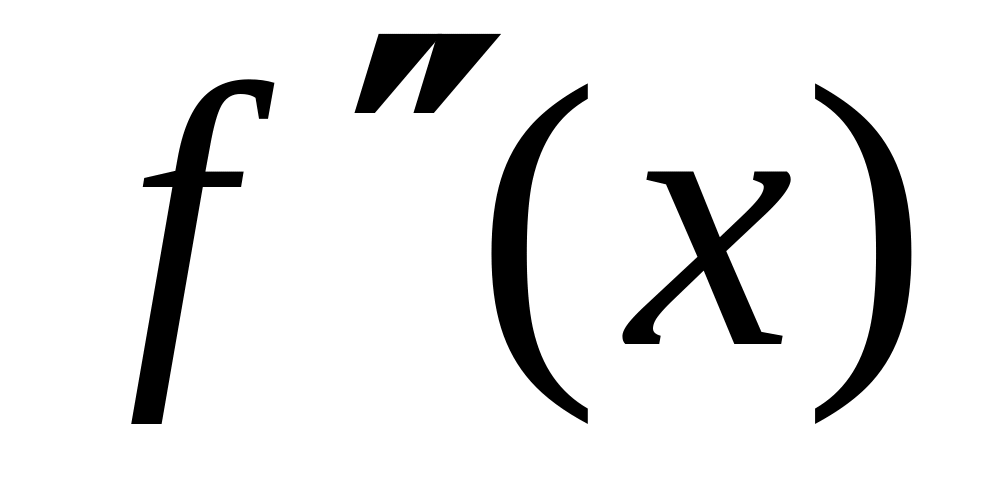по обе стороны от каждой критической точки и сделать вывод о промежутках выпуклости и точках перегиба.

5. Найти значения функции в точках перегиба и точки перегиба графика.

Ниже приведены примеры, в которых продолжены исследования функций, рассмотренных в примерах (3.35)−(3.39).

Пример 3.40. Найти промежутки выпуклости и точки перегиба функции

□ 1. Область определения .

2. Найдем вторую производную:

3 . Найдем критические точки 2-го рода:

4. Исследуем знак второй производной. Так как при , то функция выпукла вниз на этих промежутках. Так как при , то функция выпукла вверх на этом отрезке. При переходе через точки вторая производная меняет знак. Поэтому эти точки являются точками перегиба функции.

Н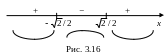 а рис. 3.16 указываем направления выпуклости графика. Обе критические точки являются точками перегиба, так как они разделяют интервалы, в которых функция выпукла вниз и вверх.

5. Вычисляем значения функции в точках перегиба: Точки перегиба графика: ■

Пример 3.41. Найти промежутки выпуклости и точки перегиба функции

□ 1. Область определения .

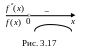2. Найдем вторую производную:

3. В области определения критических точек

2-го рода нет, так как при .

4. Знак второй производной отрицательный во всей области определения. Следовательно, функция выпукла вверх во всей области определения . Точек перегиба нет.

5. − ■

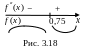Пример 3.42. Найти промежутки выпуклости и точки перегиба функции

□ 1. 2.

3.

4. Определим знаки второй производной:

(см. рис.3.18).

Функция выпукла вниз при выпукла вверх при Точка − точка перегиба функции.

5. Точка перегиба графика имеет координаты ■

Пример 3.43. Найти промежутки выпуклости и точки перегиба функции

□ 1. Область определения

2. Найдем вторую производную:

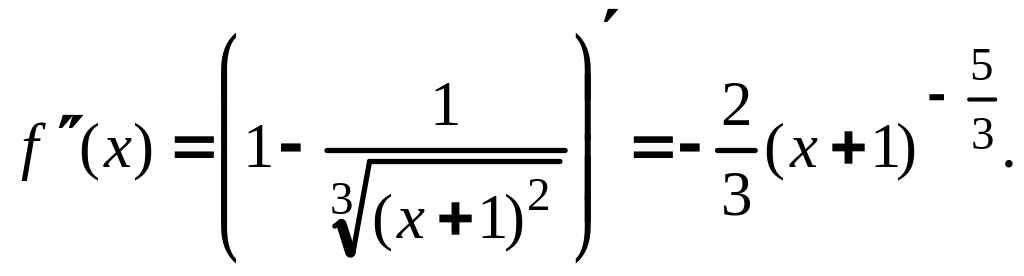
3. Критическая точка 2-го рода находится из условия: Отсюда − критическая точка 2-го рода.

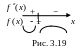4. Исследуем знаки второй производной и получим: Следовательно, функция выпукла вниз на промежутке и выпукла вверх на промежутке Точка является точкой перегиба.

5. Точка перегиба графика имеет координаты ■