
- •Предисловие
- •Глава 1 принципы построения систем
- •1.1. Преобразование сигналов в цифровых системах передачи
- •1.2. Импульсная модуляция
- •1.3. Принципы временного разделения каналов
- •1.4. Принципы построения радиосистем с врк
- •Глава 2 цифровые виды модуляции
- •2.1. Импульсно-кодовая модуляция
- •2.2. Дифференциальная импульсно-кодовая модуляция
- •2.3. Дельта-модуляция
- •2.4. Дельта-модуляция с компандированием
- •Глава 3 аппаратура оконечной станции икм-врк
- •3.1. Основы построения оконечной станции икм-врк и временного цикла передачи
- •3.2. Амплитудно-импульсные модуляторы и временные селекторы
- •3.3. Кодеры и декодеры с линейной шкалой квантования
- •3.4. Кодеры и декодеры с нелинейной шкалой квантования
- •3.5. Генераторное оборудование
- •3.6. Тактовая синхронизация. Выделение тактовой частоты
- •3.7. Цикловая синхронизация
- •3.8. Принципы организации каналов передачи сув
- •Глава 4 линейный тракт цсп
- •4.1. Особенности передачи цифровых сигналов по линейным трактам. Линейные коды цсп
- •4.2. Регенераторы цифровых сигналов
- •4.3. Накопление помех в цифровом линейном тракте
- •Глава 5 объединение и разделение цифровых потоков
- •5.1. Стандартизация цифровых систем передачи
- •5.2. Временное объединение цифровых потоков
- •5.3. Оборудование временного группообразования асинхронных цифровых потоков
- •5.4. Оборудование асинхронного объединения цифровых потоков
- •5.5. Оборудование временного группообразования синхронных цифровых потоков
- •5.6. Выделение цифровых потоков
- •5.7. Ввод дискретной информации в групповой цифровой поток
- •Г л а в а 6 первичные цифровые системы передачи икм-30 и икм-зос
- •6.1. Общие сведения о икм-30
- •6.2. Аналого-цифровое оборудование икм-30
- •6.3. Линейное оборудование оконечной станции
- •6.4. Линейный тракт. Регенераторы
- •6.5. Система телеконтроля работы линейного тракта
- •6.6. Система передачи икм-зос
- •Глава 7 система передачи икм-15
- •7.1. Общие сведения
- •7.3. Оборудование линейного тракта
- •7.4. Система передачи «зона-15»
- •Глава 8 система передачи икм-120
- •8.1. Общие сведения
- •8.2. Оборудование ацо-чд-60
- •8.3. Оборудование вторичного временного группообразования
- •8.4. Оборудование линейного тракта
- •Г л а в а 9 цифровые системы передачи внутризоновых и магистральных сетей связи
- •9.1. Система передачи икм-480
- •9.2. Система передачи икм-1920
- •Глава 10 проектирование каналов тч цифровых систем передачи
- •10.1 Принципы проектирования линейных трактов цсп
- •10.2. Проектирование дсп на местных сетях
- •10.3. Проектирование цсп на зоновых и магистральных сетях
- •Глава 11 техническое обслуживание дсп
- •11.1. Параметры каналов и трактов цсп
- •11.2. Измерения параметров каналов цсп
- •11.3. Настройка и эксплуатация цсп
1.2. Импульсная модуляция
Теорема
Котелынкова.
Возможность
передачи непрерывного сигнала его
дискретными отсчетами была обоснована
В. А. Котельниковым в
1933
г. В соответствии с его теоремой любой
непрерывный сигнал, ограниченный по
спектру верхней частотой
FB,
полностью
определяется последовательностью своих
дискретных отсчетов, взятых через
промежуток времени
Tд![]() 1/2FB.
1/2FB.
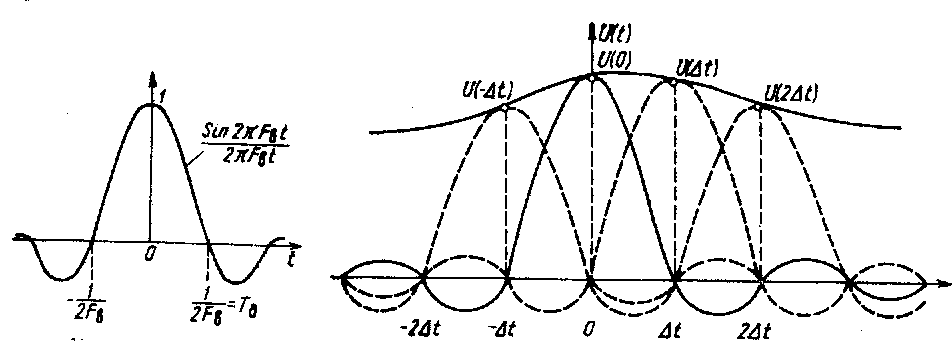
Рис. 1.6 Отклик ФНЧ на Рис. 1.7. Формирование непрерывного сигнала
короткий прямоугольный фильтром нижних частот
импульс
Таким
образом, если требуется передать
непрерывный сигнал U
(г)
с ограниченным спектром, то не обязательно
передавать весь сигнал, а достаточно
передать лишь его мгновенные значения,
отсчитанные через интервалы времени
7Д
(см. рис.
1.1).
В соответствии с этим частота
следования дискретных отсчетов сигнала,
т. е.
частота
дискретизации
Fд![]() 2FB.
2FB.
Для восстановления непрерывного сигнала из последовательности его дискретных отсчетов в пункте приема используется фильтр нижних частот (ФНЧ) с частотой среза, равной Fa.
Как известно, отклик идеального ФНЧ с граничной частотой среза FB на очень короткий прямоугольный импульс, поданный на его вход, имеет вид, изображенный на рис. 1.6.
Если на вход такого фильтра поступает последовательность коротких импульсов, соответствующих дискретным отсчетам непрерывного сигнала (рис. 1.7), то на выходе фильтра в результате суммирования отдельных откликов переданный непрерывный сигнал вновь восстанавливается.
Параметры импульсной последовательности. Последовательность прямоугольных импульсов одного знака (рис. 1.8, а) характеризуется следующими параметрами: амплитудой U, длительность импульса Ти, периодом следования Тс, частотой следования Fc — 1/Тс, круговой частотой следования ωс= 2nFc — 2л/Тс, скважностью <Q = Tc/τн.
Частотный спектр такой последовательности импульсов при постоянных параметрах является дискретным, т. е. состоящим из отдельных частот, кратных частоте следования импульсов (рис. 1.8, б), а также содержит постоянную составляющую, значение которой зависит от скважности Q и амплитуды импульсов U и определяется как U0= Uτн/Тс.
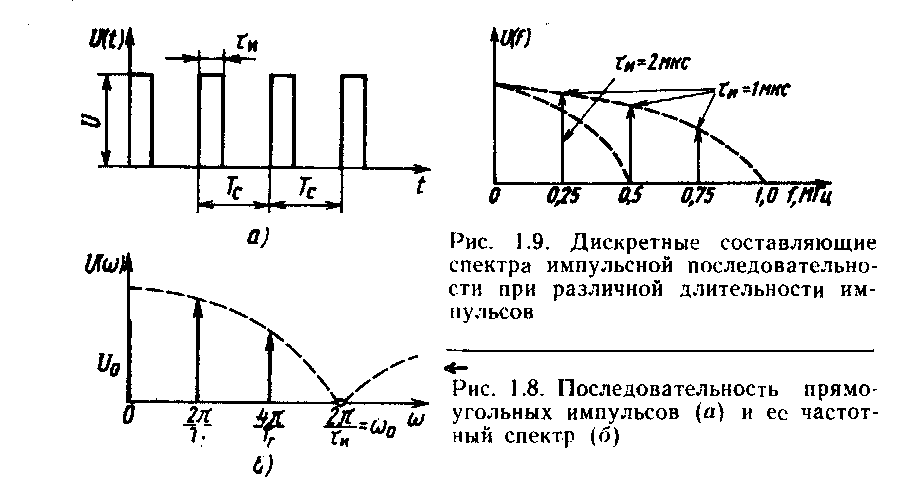
Ширина частотного спектра импульсной последовательности при допустимых искажениях их формы может быть ограничена частотой, зависящей от длительности импульса ω0 = 2π/τи или ƒо=l/τи. Таким образом, чем короче импульс, т. е. чем меньше его длительность, тем шире его частотный спектр и тем больше гармоник частоты следования содержится в его спектре.
Амплитуда частоты следования или ее гармоник может быть определена из формулы
![]()
Пример. Задана импульсная последовательность с параметрами τи = 1 мкс, τс=4 мкс, l/0 = 4 В. Определить: частоту следования Fc; ширину спектра Δ.F= ƒ0; постоянную составляющую U0; дискретные составляющие спектра. Нарисовать частотный спектр последовательности и частотный спектр, если ти=2мкс.
По приведенным выше формулам находим: Fc = 1/T с =250 кГц; ΔF = l/τи = МГц; Uo=Uτn/Tc=1 В; дискретные составляющие спектра Fс = 250кГц, 2FC=500 кГц; 3Fc=750 кГц (рис. 1.9). При τн=2 мкс, ΔF1 = 500 кГц и Fc = 250 кГц (см. рис. 1.9).
Амплитудно-импульсная модуляцияю. При изменении амплитуды, длительности, частоты следования или положения каждого импульса во времени по отношению к моментам отсчета (дискретизации) получают тот или иной вид импульсной модуляции. При амплитудно-импульсной модуляции (АИМ) по закону модулирующего сигнала изменяется амплитуда импульсов, а длительность и частота следования остаются постоянными.
Различают АИМ первого и второго рода (АИМ-1, АИМ-2). При АИМ-1 амплитуда импульса изменяется в пределах его дли-
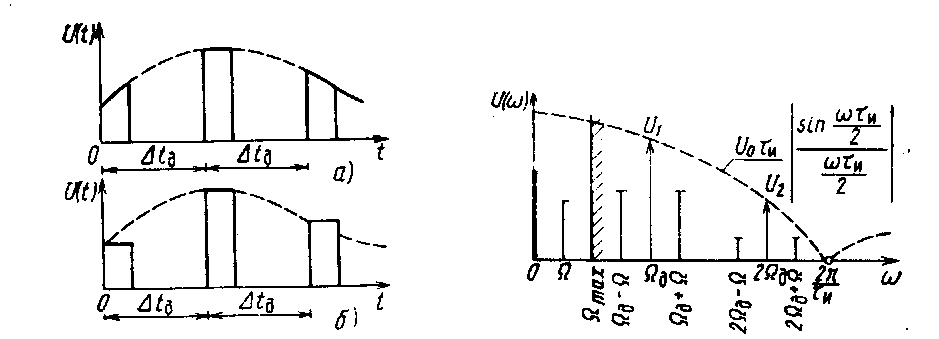 Рис.
1.10.
Форма сигнала при АИМ-1 Рис.
1.11.
Частотный спектр АИМ при (а) и АИМ-2 (б)
гармоническом
модулирующем сигна-
Рис.
1.10.
Форма сигнала при АИМ-1 Рис.
1.11.
Частотный спектр АИМ при (а) и АИМ-2 (б)
гармоническом
модулирующем сигна-
ле
тельности в соответствии с огибающей непрерывного сигнала (рис. 1.10, а). При АИМ-2 амплитуда импульса в пределах его длительности постоянна и соответствует значению модулирующего сигнала в момент начала отсчета (рис. 1.10, б). Частотный спектр АИМ-1 для однополярных прямоугольных импульсов длительностью ти, модулированных синусоидальным сигналом с частотой QM, показан на рис. 1.11. Как видно, в отличие от немодулирован-ной импульсной последовательности (см. рис. 1.8,6), в спектре появляются боковые частоты около частоты дискретизации и ее гармоник, а также спектр модулирующего сигнала. Таким образом, задача восстановления непрерывного сигнала из последовательности его дискретных отсчетов заключается в фильтрации спектра модулирующего сигнала Qc с помощью ФНЧ с частотой среза
При дискретизации сложного сигнала со сплошным спектром частотные спектры сигналов АИМ-1, АИМ-2 (рис. 1.12) будут содержать все составляющие модулирующего сигнала и боковые полосы частот около частоты дискретизации и ее гармоник. При этом следует обратить внимание на различие частотных спектров АИМ-1 и АИМ-2. Спектральный состав сигналов АИМ-2 по своей
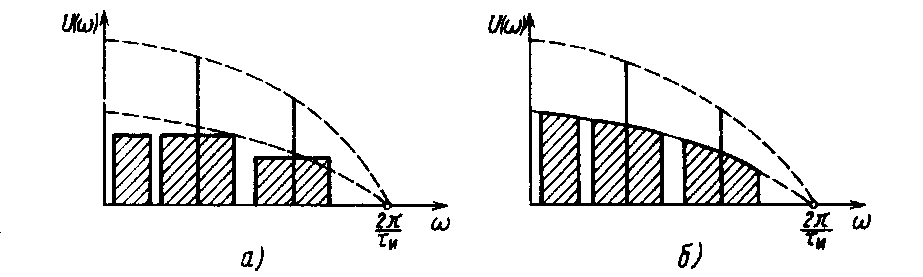
Рис. 1.12. Частотные спектры сигналов АИМ-1 (а) и АИМ-2 (б)
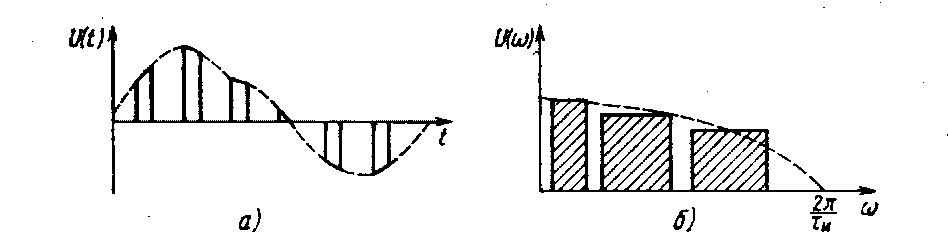
Рис. 1.13. Амплитудно-импульсная модуляция разнополярных отсчетов (а) и ее частотный спектр (б)
структуре (рис. 1.12,6) не отличается от структуры спектра сигналов АИМ-1 (рис. 1.12, а), однако при АИМ-2 изменение спектральных составляющих модулирующего сигнала и боковых полос зависит от длительности импульса ти, что в принципе приводит к амплитудно-частотным искажениям демодулированного из АИМ-2 сигнала при ти>0,27,д. В реальных ЦСП ти<0,17,д и спектры совпадают практически полностью, а амплитудно-частотные искажения при демодуляции сигналов АИМ-2 незначительны.
При дискретизации сигналов телефонных сообщений и сигналов вещания дискретные отсчеты представляют собой последовательности разнополярных импульсов переменной амплитуды (рис. 1.13,а). При таком виде АИМ сигналов в их спектре отсутствуют составляющие частоты дискретизации и ее гармоник (рис. 1.13,6).
Выбор частоты дискретизации. На основании теоремы Котель-никова F^2FB. Если выбрать Fa=2FB, то, как видно из рис. 1.14, а, нижняя боковая частота, определяемая из условия Рл—FB = 2Fb— —FB = FB, совпадает с верхней частотой спектра модулирующего сигнала и для восстановления непрерывного сигнала из последовательности его дискретных отсчетов необходимо использовать идеальный ФНЧ с частотой среза FQ = FB. В реальных системах частоту дискретизации выбирают из условия Fz>2FB. Обычно Fa = (2,3...2,4)74. Так, при дискретизации телефонных сигналов с диапазоном частот 0,3...3,4 кГц частота дискретизации равна 8 кГц.
Как видно из рис. 1.14,6, в данном случае упрощаются требования к параметрам ФНЧ, так как при этом образуется достаточ
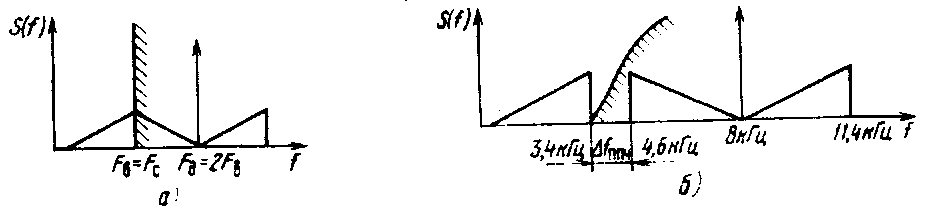
Рнс. 1.14. Выбор частоты дискретизации 10
но широкая (1,2 кГц) переходная полоса частот Д/ппч для рас-фильтровки, которая позволяет использовать простые ФНЧ на приеме для восстановления непрерывного сигнала из последовательности его дискретных отсчетов.
Пример. Выбрать частоту дискретизации и определить переходную полосу частот для ФНЧ при дискретизации сигналов вещания первого класса с диапазоном частот 0,05 ... 10 кГц.
На основании теоремы Котельникова F^^2Fe, следовательно, в нашем случае F„>20 кГц. Для телефонного сигнала стандартная частота дискретизации Fa=8 кГц. При организации канала вещания (вместо трех телефонных каналов) частота дискретизации сигналов вещания должна быть кратна частоте дискретизации телефонного канала и равна 8X3 = 24 кГц. Переходная полоса частот для ФНЧ Д/ппч = 4 кГц.
Выбор частоты дискретизации группового сигнала. При построении систем ИКМ—ЧРК осуществляется дискретизация сигналов, диапазон частот которых соответствует диапазону частот стандартных групп в системах с ЧРК.
Рассмотрим вопросы выбора частоты дискретизации первичной стандартной 12-канальной группы со спектром частот 60... 108 кГц. Диапазон частот группы ограничен не только сверху, но и снизу. Поэтому частоту дискретизации в этом случае выбирают так, чтобы в спектре АИМ сигнала спектр дискретизируемо-го сигнала не перекрывался с боковыми спектрами около частоты дискретизации и ее гармоник (рис. 1.15). Для сигнала первичной стандартной 12-канальной группы при Fa=ll0 кГц (рис. 1.15) спектр АИМ сигнала содержит спектр дискретизируемого сигнала в диапазоне частот 60...108 кГц, нижнюю боковую полосу около частоты дискретизации, определяемую из условия AF„6i=FA— (/=,H...FB) = 110 кГц — (60...108) кГц=(2...50) кГц, верхнюю боковую полосу около частоты дискретизации АРвы=Рд+ (FH...FB) = = 110 кГц+(60...108) кГц= (170...218) кГц, нижнюю боковую полосу второй гармоники частоты дискретизации AFn62 = 2FM—
— (F„...FB)=220 кГц-(60...108) кГц= (112...160) кГц, верхнюю боковую полосу второй гармоники частоты дискретизации AF„62 = =2F«-r-(F„...FB)=220 кГц+(60...108) кГц= (280...328) кГц.
Как видно из рис. 1.15, спектр полезного сигнала и спектры около частоты дискретизации и ее гармоник не перекрываются.
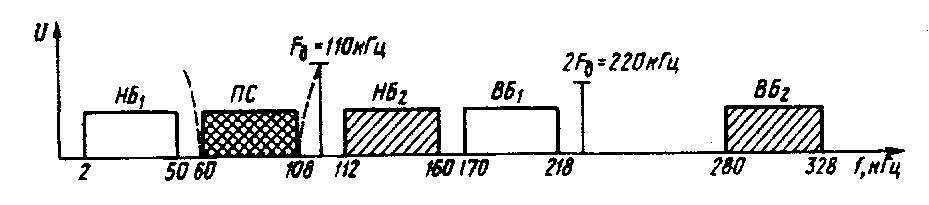
Рис. 1.15. Составляющие спектра сигнала при дискретизации первичной 12-канальной группы
При таком выборе частоты дискретизации можно осуществить Восстановление без искажений информационного сигнала из последовательности его отсчетов с помощью полосового фильтра ПФ с полосой пропускания 60... 108 кГц.
Увеличение частоты дискретизации приводит к росту верхней частоты нижней боковой полосы НБ1 и в пределе, при отсутствии перекрытия спектров НБ1 и информационного сигнала, верхняя частота нижней боковой полосы равна 60 кГц. Из этого следует, что при дискретизации групповых сигналов, ширина спектра которых &F<iFn (48<60 кГц для 12-канальной группы), частота дискретизации выбирается из условия FB<.Fg,-<.2FH. Для упрощения реализации ПФ, восстанавливающих непрерывный сигнал, Fa выбирается в середине диапазона 108... 120 кГц для первичной стандартной 12-канальной группы.
Если ширина спектра группового сигнала AF>FH, как, например, для третичной стандартной 300-канальной группы со спектром частот 812...2044 кГц, то частоту дискретизации можно выбрать из условия Fa>2FB, однако при этом не используется нижняя часть полосы частот до 812 кГц, что приводит к дополнительному расширению спектре АИМ сигнала. Для того чтобы исключить такое расширение спектра, вводят дополнительную ступень преобразования, с помощью которой спектр сигнала 300-канальной группы смещается вниз по оси частот в диапазон 60... 1292 кГц. Это дает возможность снизить частоту дискретизации и выбрать ее из условия /7Д>2584 кГц.
Пример. Рассчитать частоту дискретизации группового сигнала вторичной стандартной 60-канальной группы.
Ширина спектра частот группы 312 ... 552 кГц, Af=240 кГц, FH = 312 кГц, FB = 552 кГц. Из условия FB<Fn<2F„ находим, что Fa = 600 кГц.
Широтно- и временная импульсная модуляции. В системах связи с ВРК кроме АИМ используются и другие виды импульсной модуляции. При широтно-импульсной модуляции (ШИМ) длительность импульсов изменяется пропорционально величине модулирующего сигнала, а их амплитуда и положение по отношению к тактовым точкам остаются постоянными (рис. 1.16).
Различают одностороннюю и двустороннюю ШИМ. При односторонней ШИМ длительность импульса относительно тактового момента изменяется из-за перемещения одного из его фронтов (см. рис. 1.16, а). При двусторонней ШИМ относительно тактовых точек перемещаются оба фронта импульса (см. рис. 1.16,6).
Частотный спектр ШИМ сигнала при модуляции гармоническим сигналом содержит полезный сигнал и ряд нижних и верхних боковых частот около Fn и ее гармоник (рис. 1.17). Так же как и при АИМ, восстановление (демодуляция) непрерывного первичного сигнала при ШИМ осуществляется ФНЧ с частотой среза Qc. Однако в этом случае из-за наличия ряда нижних боковых составляющих (шд—Qc; о>д—2йс; о>д—Зйс, ... и т. д.) некоторые боковые составляющие, например шд—3QC, могут попадать в полосу пропускания ФНЧ, что приводит к комбинационным искажениям демодулированного сигнала
12
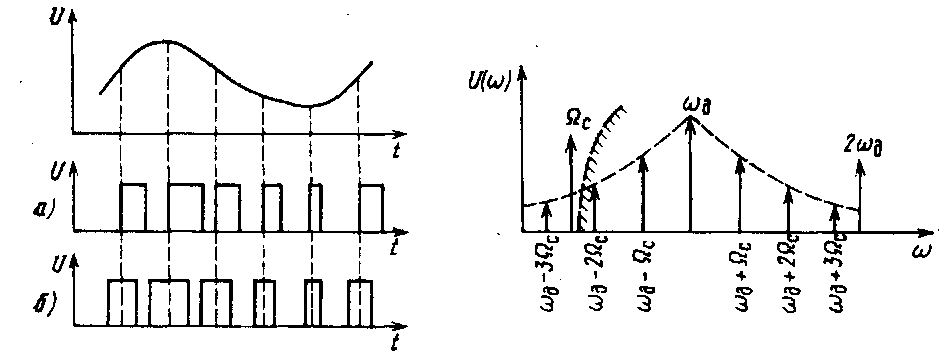
Рис. 1.16. Широтно-импульсная мо- Рис. 1.17. Спектр ШИМ
модуляция:
а — односторонняя; б — двусторонняя
.
При временной импульсной модуляции (ВИМ) под воздействием модулирующего напряжения изменяется временное положение импульсов относительно тактовых точек, но их амплитуда и длительность остаются неизменными. Разновидностями ВИМ являются фазово-импульсная (ФИМ) и частотно-импульсная (ЧИМ) модуляция.
По своему частотному составу спектры ШИМ, ФИМ и ЧИМ аналогичны, поэтому для всех видов импульсной модуляции при восстановлении (демодуляции) непрерывного сигнала с помощью ФНЧ характерно наличие комбинационных искажений.
