Расстояние от точки до плоскости

9. Расстояние от точки до плоскости с нормальным вектором вычисляется по формуле: .

Различные виды уравнений прямой в пространстве

10. Общие уравнения прямой: где и – плоскости с нормальными векторами и .

11. Канонические уравнения прямой: , где вектор – направляющий вектор прямой, – произвольная точка прямой.

12. Уравнения прямой, проходящей через две данные точки и : .

13. Параметрические уравнения прямой: 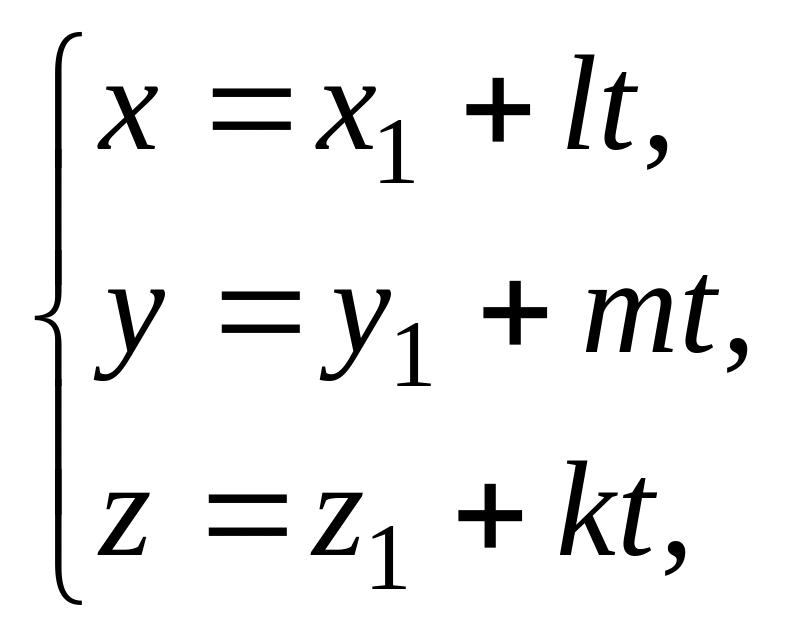где – параметр, – направляющий вектор прямой, – произвольная точка прямой.

Взаимное расположение двух прямых в пространстве

14. Угол между прямой с направляющим вектором и прямой с направляющим вектором вычисляется по формуле: .

15. Условие параллельности двух прямых в пространстве: прямая с направляющим вектором и прямая с направляющим вектором параллельны тогда и только тогда, когда .

16. Условие перпендикулярности двух прямых в пространстве: прямая с направляющим вектором и прямая с направляющим вектором перпендикулярны тогда и только тогда, когда .

Взаимное расположение прямой с плоскостью

17. Угол между прямой с направляющим вектором и плоскостью с нормальным вектором вычисляется по формуле .

18. Условие параллельности прямой и плоскости: прямая с направляющим вектором и плоскость с нормальным вектором параллельны тогда и только тогда, когда .

19. Условие перпендикулярности прямой и плоскости: прямая с направляющим вектором и плоскость с нормальным вектором перпендикулярны тогда и только тогда, когда .

20. Условие принадлежности двух прямых одной плоскости: прямые с направляющим вектором и с направляющим вектором принадлежат плоскости тогда и только тогда, когда . Если при этом нарушается хотя бы одна из пропорций , то прямые пересекаются. В противном случае эти прямые параллельны.

21. Условия принадлежности прямой к плоскости: прямая с направляющим вектором принадлежит плоскости с нормальным вектором тогда и только тогда, когда выполняются равенства и .

1.3. Образец решения контрольной работы № 1.

Задание 1. Даны вершины А(–1; 0), В(5; 2), С(2; 4) треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А. Сделать чертеж.

Р ешение. Изобразим заданный треугольник в декартовой системе координат Oxy.

1) Длину стороны АВ найдем, используя формулу расстояния между двумя точками на плоскости: .

Подставляя в нее координаты точек А(–1; 0) и В(5; 2), получим:  (ед.).

2) По определению медианы точка М медианы CМ делит сторону АВ пополам. Следовательно, ее координаты определяются по формулам деления отрезка пополам:

, .

Таким образом, найдена точка М(2; 1).

Уравнение медианы CМ найдем как уравнение прямой, проходящей через две заданные точки C и М, по формуле: или , или .

По свойству пропорции отсюда следует уравнение CМ:

или .

3) Уравнение высоты СH как прямой, проходящей через точку С перпендикулярно стороне АВ, будем искать в виде , где угловой коэффициент найдем из условия перпендикулярности прямых СH и АВ: .

Угловой коэффициент определим, используя формулу углового коэффициента прямой: . Следовательно, .

Уравнение высоты примет теперь вид: или .

4) Аналогично, уравнение прямой L, проходящей через вершину С параллельно стороне АВ, будем искать в виде: , где угловой коэффициент прямой L найдем из условия параллельности прямых L и AB: .

Уравнение прямой L примет вид: или .

5) Длину высоты СН найдем, используя формулу расстояния от точки С до прямой АВ: , где есть общее уравнение стороны АВ.

Найдем уравнение стороны АВ: или , или .

Подставляя в найденное уравнение координаты точки С, получим:  (ед.).

6) Из рисунка видно, что внутренний угол А треугольника АВС есть угол, на который нужно повернуть сторону АВ в положительном направлении (т. е. против часовой стрелки) до совмещения ее со стороной АС. Поэтому тангенс угла А найдем по формуле: .

Угловой коэффициент (найден в п. 3). Аналогично найдем . Следовательно, , тогда  (рад.).

Ответ: 1) длина стороны АВ:  ед.; 2) уравнение медианы CМ: ; 3) уравнение высоты СН: ; 4) уравнение прямой L: ; 5) длина высоты СН:  ед.; 6) величина внутреннего угла А:  рад.

Задание 2. Составить уравнение и построить линию, для каждой точки которой выполняется следующее условие: отношение расстояний до точки F(–1; 0) и прямой равно .

Решение. Сделаем схематический чертеж по условию задачи.

1) Предположим, что М(x; y) – текущая точка искомой линии. Тогда точка N(–4; y) является ее проекцией на прямой x = –4.

2) По условию задачи выполняется следующее отношение расстояний: или .

3) Используя формулу расстояния между двумя точками, выразим полученное буквенное равенство в координатной форме и преобразуем его к виду канонического уравнения одной из кривых второго порядка (окружности, эллипса, гиперболы или параболы):

или , или .

Получили каноническое уравнение эллипса: , у которого полуоси есть и .

4) Построим линию по ее уравнению.

Ответ:  эллипс.

Задание 3. Написать разложение вектора по векторам , , .

Решение. Требуется представить вектор в виде , где ,  и  – неизвестные числа. Согласно определения произведения вектора на число и суммы векторов имеем: , , и . Применяя определение равенства двух векторов получим линейную систему трех уравнений относительно неизвестных , , : которую решим по формулам Крамера. Для этого составим четыре определителя 3-го порядка и вычислим их по правилу треугольников:

.

Т. к. , то система имеет единственное решение.

.

.

.

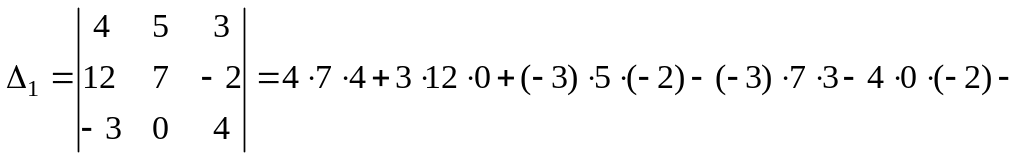
Т. о., по формулам Крамера: , , .

Ответ:  .

Задание 4. Даны вершины A₁(1; –1; 2), A₂(2; 1; 2), A₃(1; 1; 4), A₄(6; –3; 8) пирамиды A₁A₂A₃A₄. Найти: 1) величину угла между ребрами A₁A₃ и A₁A₄; 2) площадь грани A₁A₂A₃; 3) уравнение плоскости, содержащей грань A₁A₂A₃; 4) уравнение высоты пирамиды, проведенной через вершину A₄. Сделать схематический чертеж.

Р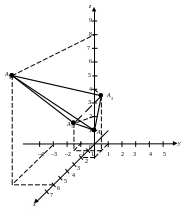 ешение. Сделаем схематический чертеж.

1) Найдем векторы и , проходящие через 2 заданные точки:

,

.

Находим косинус угла между векторами по формуле:

. Следовательно,  (рад.).

2) Гранью A₁A₂A₃ пирамиды A₁A₂A₃A₄ является треугольник A₁A₂A₃, площадь которого определим по формуле: .

Координаты вектора (см. п. 1). Аналогично найдем координаты вектора .

Вычислим теперь векторное произведение векторов и :

.

Тогда длина векторного произведения равна:

.

Т. о., получим:  (кв. ед.).

3) Уравнение искомой плоскости составим как уравнение плоскости, проходящей через три данные точки A₁, A₂, A₃ в форме определителя 3-го порядка: или , или 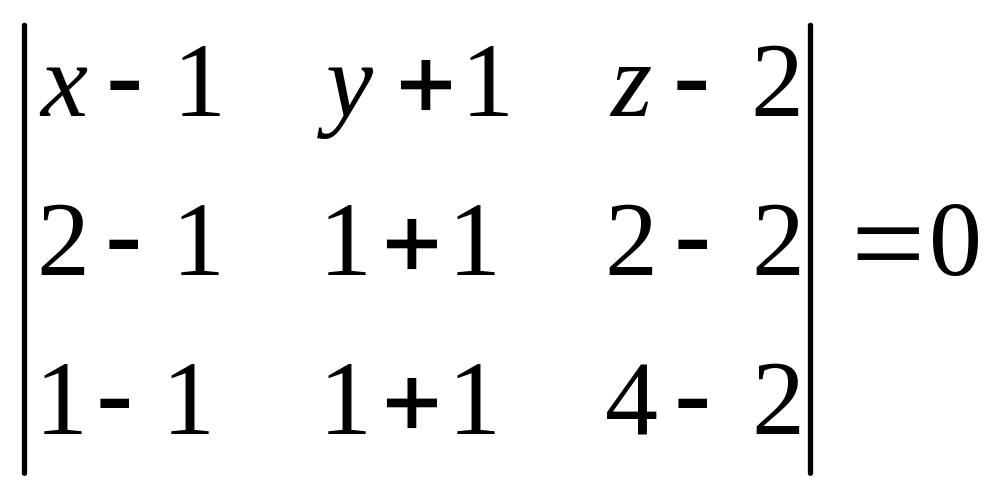, или

, или , или .

4) Уравнение высоты, опущенной из точки А₄ на грань А₁А₂А₃ найдем как прямую, проходящую через точку А₄ перпендикулярно плоскости А₁А₂А₃ в форме канонических уравнений прямой , где вектор является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А₁А₂А₃: , следовательно, ее нормальным вектором является вектор . Т. к. вектор коллинеарен высоте, то его можно выбрать в качестве направляющего вектора прямой. Следовательно, искомое уравнение высоты имеет вид: .

Ответ: 1) величина угла между ребрами A₁A₃ и A₁A₄:  рад.; 2) площадь грани A₁A₂A₃:  кв. ед.; 3) уравнение плоскости A₁A₂A₃: ; 4) уравнение высоты из вершины A₄: .