3. Дифференциальное исчисление функций нескольких переменных Явное задание функции

1. Если , а и , то . В частности, если , а совпадает с одним из аргументов, например, , то .

2. Если , а и , то и . Структура этих формул сохраняется и при большем числе переменных.

Неявное задание функции

3. Если уравнение задает неявно функцию , то и , где . В частности, если уравнение неявно определяет функцию , то .

Касательная плоскость и нормаль к поверхности

4. Частные производные , функции двух переменных находятся по обычным правилам и формулам дифференцирования по каждой из переменной при фиксированном значении второй переменной. Например: ; .

5. Если поверхность задана явно функцией , то уравнение касательной плоскости в точке : ; уравнение нормали в точке : .

6. Если поверхность задана неявно уравнением , то уравнение касательной плоскости в точке : уравнение нормали в точке : .

7. Полный дифференциал функции находится по формуле: . Дифференциал второго порядка равен: .

8. Если дифференциалы и независимых переменных достаточно малы, дифференциал функции приближенно равен ее приращению: . Отсюда следует, что приближенное значение в точке можно найти по формуле: , где , , а значения частных производных вычисляются в точке . Если обозначить через , то абсолютная погрешность , относительная погрешность .

9. Производная функции по направлению вектора вычисляется по формуле: .

10. Градиент функции есть вектор с координатами .

Экстремум функции двух переменных

11. Необходимые условия экстремума функции :

12. Достаточные условия экстремума функции :

а) если и , то – точка максимума;

б) если и , то – точка минимума;

в) если , то не является точкой экстремума;

г) если , то может быть или не быть точкой экстремума, поэтому требуется дополнительное исследование.

Здесь , где , , .

13. Для нахождения наибольшего и наименьшего значения функции в замкнутой области, ограниченной данными линиями, надо сначала найти критические точки этой функции, расположенные внутри данной области. Для этого надо решить систему и выбрать среди решений те точки, которые лежат внутри области. Затем надо исследовать поведение функции на границе области. На каждом отрезке границы (не обязательно прямолинейной) можно выразить одну из независимых переменных через другую и, подставив то выражение в функцию , получить как функцию одной переменной. Найдя все критические точки на границе области, сравниваем значения функции во всех критических точках (внутри и на границы области) и в угловых точках границы. Выбираем из этих значений наибольшее и наименьшее.

2.3. Образец решения контрольной работы № 2.

Задание 1. Найти пределы функций.

1)

2) ; 3) .

Решение. 1) Данный предел в зависимости от значений вычисляется разными способами.

а)  . Найдем значения функций, стоящих в числителе и в знаменателе дроби, в точке : . Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке: ;

б)  . Найдем новые значения и в точке : . Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке является неопределенностью вида и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель , создающий неопределенность вида при . С этой целью найдем корни уравнений и , затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):

;

в)  . При имеем и , т. е. заданное отношение при является неопределенностью вида и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной . В данном случае это есть . После сокращения дроби на критический множитель применим теорему о пределе частного и следующие равенства, известные из теории пределов: , , .

Получим:

.

2) Найдем значения функций и , стоящих в числителе и знаменателе дроби, в точке : , . Следовательно, заданное отношение при является неопределенностью вида . Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель , создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю и используем формулу сокращенного умножения разности квадратов: :

.

По теореме о пределе корня , получим:

.

3)  . Найдем значения функций и в точке : и . Следовательно, заданное отношение представляет собой при неопределенность вида . Вычислим этот предел, применяя формулу первого замечательного предела: и равенство , вытекающее из непрерывности в точке функции . С этой целью преобразуем заданный предел следующим образом:

.

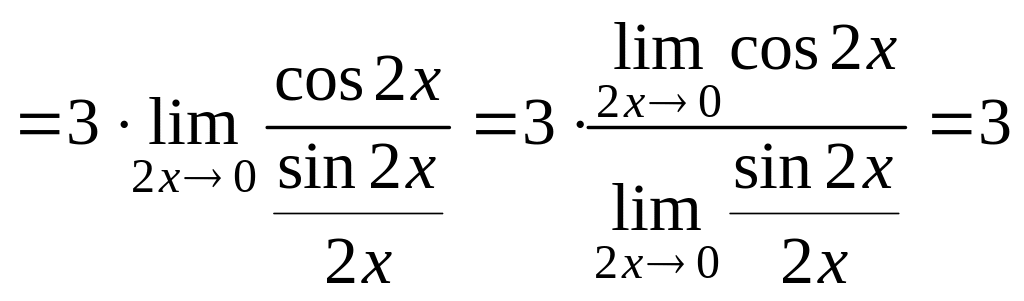Ответ: 1), а) ; б) ; в) . 2)  . 3) 3.

Задание 2. Найти производные заданных функций.

1) ; 2) ;

3) .

Решение. 1) .

Используем правило дифференцирование суммы и правила дифференцирования сложной функции вида , где , а также таблицу производных. Получим:

.

2)  .

Используем правило дифференцирование суммы и правила дифференцирования сложных функций вида

,

где , а также таблицу производных. Получим:

.

3)  .

Используем правило дифференцирования суммы , правило дифференцирования произведения и правила дифференцирования сложных функций вида

,

где , а также таблицу производных. Получим:

.

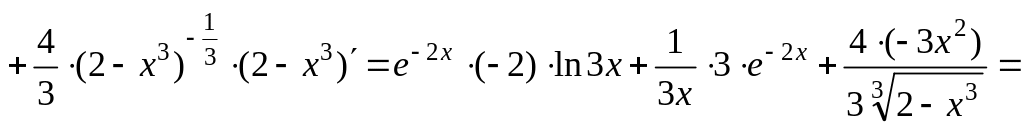
Ответ: 1)  ; 2)  ; 3)  .

Задание 3. Провести полное исследование функции и построить ее график.

Решение. 1) Найдем область определения, интервалы непрерывности и точки разрыва функции.

Функция определена на всей числовой оси, кроме точки , т. е. . В каждой точке области определения функция непрерывна. Точка есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.

2) Выясним четность, нечетность и периодичность функции.

, т. е. . Следовательно, функция не является ни четной, ни нечетной.

Функция непериодична, т. к. , где Т – некоторое действительное число.

3) Найдем асимптоты графика функции (вертикальные, горизонтальные и наклонные).

а

) Вертикальные асимптоты.

Так как точка оси Ox есть точка разрыва функции, то прямая линия , перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки близкое значение, например, и вычислим в нем значение функции и ее знак:

.

Так как это значение отрицательно, и функция слева от точки непрерывна, то она сохраняет знак и .

Теперь возьмем справа от точки близкое значение, например, :

.

Так как это значение положительно, и функция справа от точки непрерывна, то при переходе к пределу функция сохраняет знак и .

Таким образом, слева от точки функция отрицательна, а справа от точки – положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции).

б) Горизонтальные асимптоты.

Для нахождения горизонтальной асимптоты нужно найти предел функции при , раскрывая неопределенность вида . Если существует конечный предел , то прямая, определяемая уравнением , есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:

.

Предел равен бесконечности, значит горизонтальной асимптоты нет.

в) Наклонные асимптоты.

Наклонная асимптота имеет уравнение прямой линии с угловым коэффициентом вида , где , . Если , то наклонной асимптоты не существует.

Найдем оба указанных предела для заданной функции:

,

.

Таким образом, график имеет наклонную асимптоту .

4) Найдем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции.

Находим сначала первую производную функции:

.

Так как точка , в которой не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых или , т. е. .

Критические точки и точка разрыва разбивают ось Ox на 4 интервала монотонности функции. По знаку производной в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.

Таблица 1.

						1
	+	0	–	не сущ.	–	0	+
		–8 max		не сущ.		0 min	

5) Найдем интервалы выпуклости и вогнутости графика функции, точки перегиба.

Находим сначала вторую производную функции:

.

Так как точка не принадлежит области определения функции и , то критических точек второго рода нет.

Точка разрыва разбивают числовую ось Ox на 2 интервала, в которых по знаку второй производной определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.

Таблица 2.

	–	не сущ.	+
	 выпуклый	не сущ.	 вогнутый

6) Находим точки пересечения графика функции с осями координат, решая две системы уравнений.

С осью Ox:

А(1; 0) – точка пересечения графика с осью Ox.

С осью Oy:

В(0; 1) – точка пересечения графика с осью Oу.

7) Используя результаты исследования, строим график функции в такой последовательности: а) рисуем вертикальную асимптоту и наклонную асимптоту , подписываем их; б) изображаем максимум функции в точке и минимум в точке ; в) наносим на осях точки А(1; 0) и В(0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот.

Задание 4. Доказать, что функция удовлетворяет уравнению .

Решение. По определению частной производной находим , считая переменную y фиксированной постоянной величиной:

Аналогично находим частную производную считая переменную x фиксированной постоянной величиной:

Находим смешанную частную производную 2-го порядка, используя правило дифференцирования произведения двух функций:

Подставляем найденные частные производные в данное уравнение:

.

Ответ: что и требовалось доказать.