
- •Методические указания для студентов экономической специальности заочной и ускоренной форм обучения
- •Содержание
- •Часть 1. Программа курса
- •1. Элементы векторной алгебры и аналитической геометрии.
- •2. Введение в анализ. Дифференциальное исчисление.
- •3. Функции нескольких переменных.
- •4. Интегральное исчисление.
- •5. Дифференциальные уравнения.
- •6. Ряды.
- •7. Теория вероятностей.
- •8. Рекомендуемая литература.
- •Часть 2. Методические указания по самостоятельной работе
- •1. Чтение учебника.
- •2. Решение задач.
- •3. Самопроверка.
- •4. Консультации.
- •5. Контрольные работы.
- •6. Лекции и практические занятия.
- •7. Зачеты и экзамены.
- •Часть 3. Требования к оформлению контрольной работы
- •Часть 4. Контрольные задания
- •1.1. Контрольная работа № 1. «Аналитическая геометрия и векторная алгебра».
- •1.2. Основные теоретические сведения.
- •1. Аналитическая геометрия на плоскости. Простейшие задачи на плоскости
- •Различные виды уравнения прямой на плоскости
- •Расстояние от точки до прямой
- •Взаимное расположение двух прямых на плоскости
- •Кривые второго порядка
- •2. Элементы векторной алгебры.
- •3. Аналитическая геометрия в пространстве. Различные виды уравнения плоскости
- •Взаимное расположение двух плоскостей
- •Расстояние от точки до плоскости
- •Различные виды уравнений прямой в пространстве
- •Взаимное расположение двух прямых в пространстве
- •Взаимное расположение прямой с плоскостью
- •1.3. Образец решения контрольной работы № 1.
- •2.1. Контрольная работа № 2. «Введение в анализ. Дифференциальное исчисление».
- •2.2. Основные теоретические сведения.
- •1. Теория пределов Основные понятия
- •Основные теоремы о действиях над функциями, имеющими конечный предел
- •Важные исключения из теоремы
- •Замечательные пределы
- •2. Дифференциальное исчисление функций одной переменной
- •Основные правила дифференцирования
- •Геометрический смысл производной
- •Механический смысл производной
- •Применение производной
- •3. Дифференциальное исчисление функций нескольких переменных Явное задание функции
- •Неявное задание функции
- •Касательная плоскость и нормаль к поверхности
- •Экстремум функции двух переменных
- •2.3. Образец решения контрольной работы № 2.
- •3.1. Контрольная работа № 3. «Интегральное исчисление».
- •3.2. Основные теоретические сведения.
- •1. Неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •2. Определенный интеграл
- •Приложения определенного интеграла в геометрии
- •3.3. Образец решения контрольной работы № 3.
- •4.1. Контрольная работа № 4. «Дифференциальные уравнения. Ряды».
- •4.2. Основные теоретические сведения.
- •1. Дифференциальные уравнения
- •2. Ряды Числовые ряды Основные понятия
- •Положительные числовые ряды
- •Знакопеременные и знакочередующиеся ряды
- •Функциональные ряды Основные понятия
- •4.3. Образец решения контрольной работы № 4.
- •5.1. Контрольная работа № 5. «Теория вероятностей».
- •5.2. Основные теоретические сведения.
- •1. Случайные события
- •Операции над событиями
- •Элементы комбинаторики
- •Аксиомы теории вероятностей
- •Свойства вероятности
- •2. Случайные величины Дискретные случайные величины
- •Законы распределения дискретной случайной величины
- •Числовые характеристики дискретной случайной величины
- •Непрерывные случайные величины
- •Числовые характеристики непрерывной случайной величины
- •Законы распределения непрерывной случайной величины
- •5.3. Образец решения контрольной работы № 5.
- •Список литературы
4.1. Контрольная работа № 4. «Дифференциальные уравнения. Ряды».
1. Найти общее решение линейного дифференциального уравнения и частное решение, удовлетворяющее начальному условию y(x0) = y0.
1. ![]() ,
,
![]() .
2.
.
2. ![]() ,
,
![]() .
.
3. ![]() ,
y(0) = 5.
4.
,
y(0) = 5.
4. ![]() ,
y(–2) = 5.
,
y(–2) = 5.
5. ![]() ,
y(0) = 2.
6.
,
y(0) = 2.
6. ![]() ,
y(1) = e.
,
y(1) = e.
7. ![]() ,
y(3) = 1.
8.
,
y(3) = 1.
8. ![]() ,
y(0) = 2.
,
y(0) = 2.
9. ![]() ,
y(1) = 0.
10.
,
y(1) = 0.
10. ![]() ,
y(0) = 3.
,
y(0) = 3.
2. Найти
общее решение линейного неоднородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами с правой
частью специального вида и частное
решение, удовлетворяющее начальным
условиям y(x0) = y0
и
![]()
1. ![]() ,
y(0) = –2,
,
y(0) = –2,
![]() .
.
2. ![]() ,
y(0) = 3,
,
y(0) = 3,
![]() .
.
3. ![]() ,
y(0) = –3,
,
y(0) = –3,
![]() .
.
4. ![]() ,
y(0) = –1,
,
y(0) = –1,
![]() .
.
5. ![]() ,
y(0) = 1,
,
y(0) = 1,
![]() .
.
6. ![]() ,
y(0) = 2,
,
y(0) = 2,
![]() .
.
7. ![]() ,
y(0) = 2,
,
y(0) = 2,
![]() .
.
8. ![]() ,
y(0) = 3,
,
y(0) = 3,
![]() .
.
9. ![]() ,
y(0) = 0,
,
y(0) = 0,
![]() .
.
10. ![]() ,
y(0) = 0,
,
y(0) = 0,
![]() .
.
3. Написать три первых члена степенного ряда, найти его область абсолютной сходимости.
1. ![]() .
2.
.
2. ![]() .
3.
.
3. ![]() .
.
4. ![]() .
5.
.
5. ![]() .
6.
.
6. ![]() .
.
7. ![]() .
8.
.
8. ![]() .
9.
.
9. ![]() .
.
10. ![]() .
.
4. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
1. ![]() .
2.
.
2. ![]() .
3.
.
3. ![]() .
.
4. 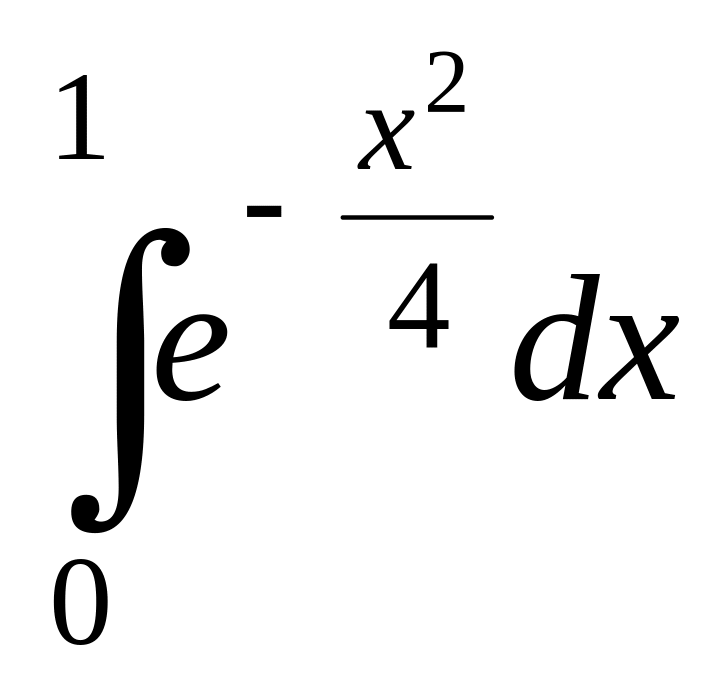 .
5.
.
5. ![]() .
6.
.
6. ![]() .
.
7. ![]() .
8.
.
8. ![]() .
9.
.
9. ![]() .
.
10. ![]() .
.
4.2. Основные теоретические сведения.
1. Дифференциальные уравнения
1. Равенство
вида
![]() ,
содержащее независимую переменную x,
искомую функцию y = y(x)
и ее производные какого-либо порядка,
называется дифференциальным
уравнением.
,
содержащее независимую переменную x,
искомую функцию y = y(x)
и ее производные какого-либо порядка,
называется дифференциальным
уравнением.
2. Натуральное число n, являющееся порядком старшей производной, называется порядком дифференциального уравнения.
3. Дифференциальным
уравнением 1-го порядка называется
уравнение вида
![]() или в дифференциалах
или в дифференциалах
![]() .
Если эти равенства можно разрешить
относительно производной, то их записывают
в виде
.
Если эти равенства можно разрешить
относительно производной, то их записывают
в виде
![]() или
или
![]() .
.
4. Решением
дифференциального уравнения 1-го порядка
называется функция y = (x),
имеющая непрерывную производную
![]() на некотором интервале (a; b)
и обращающая уравнение в верное числовое
равенство.
на некотором интервале (a; b)
и обращающая уравнение в верное числовое
равенство.
5. Задача Коши для дифференциального уравнения 1-го порядка: требуется найти решение y = (x) уравнения, удовлетворяющее начальному условию y = y0 при x = x0.
6. Общим решением дифференциального уравнения 1-го порядка называется функция y = (x; С), содержащая произвольную постоянную С и удовлетворяющая условиям: 1) при любых начальных условиях (x0; y0) уравнение y0 = (x0; С) должно быть разрешимо относительно С так, что С = (x0; y0); 2) при всех значениях постоянной С = (x0; y0) функция y = (x; (x0; y0)) должна удовлетворять дифференциальному уравнению.
7. Всякое решение, получаемое из общего при фиксированном значении постоянной С называется частным решением дифференциального уравнения.
8. Уравнение
вида
![]() или
или
![]() называется дифференциальным уравнением
с разделяющимися
переменными.
Приводятся к виду
называется дифференциальным уравнением
с разделяющимися
переменными.
Приводятся к виду
![]() или
или
![]() путем разделения переменных x
и y
и затем почленно интегрируются.
путем разделения переменных x
и y
и затем почленно интегрируются.
9. Уравнение
вида
![]() называется однородным
дифференциальным уравнением. Используется
замена:
называется однородным
дифференциальным уравнением. Используется
замена:
![]() или
или
![]() ,
где
,
где
![]() – новая неизвестная функция, тогда
– новая неизвестная функция, тогда
![]() .
Сводится к дифференциальному уравнению
с разделяющимися переменными относительно
новой функции, для которого находят
общее решение. Записывают общее решение
исходного уравнения по формуле
.
.
Сводится к дифференциальному уравнению
с разделяющимися переменными относительно
новой функции, для которого находят
общее решение. Записывают общее решение
исходного уравнения по формуле
.
10. Уравнение
вида
![]() называется линейным
дифференциальным уравнением. Используется
метод Бернулли:
называется линейным
дифференциальным уравнением. Используется
метод Бернулли:
![]() ,
где
,
,
где
,
![]() – новые неизвестные функции, тогда
– новые неизвестные функции, тогда
![]() .
Получаем:
.
Получаем:
![]() или
или
![]() .
Подберем функцию v
так, чтобы выражение в скобках было
равно нулю, тогда получаем
.
Подберем функцию v
так, чтобы выражение в скобках было
равно нулю, тогда получаем
![]() Первое уравнение – ДУ с разделяющимися
переменными, находим его частное решение
при С = 0.
Найденное частное решение подставляем
во второе уравнение, являющееся тоже
ДУ с разделяющимися переменными и
находим его общее решение. Записываем
общее решение исходного уравнения по
формуле
.
Первое уравнение – ДУ с разделяющимися
переменными, находим его частное решение
при С = 0.
Найденное частное решение подставляем
во второе уравнение, являющееся тоже
ДУ с разделяющимися переменными и
находим его общее решение. Записываем
общее решение исходного уравнения по
формуле
.
11. Уравнение
вида
![]() ,
где
,
где
![]() называется дифференциальным уравнением
Бернулли.
Используется метод Бернулли:
.
называется дифференциальным уравнением
Бернулли.
Используется метод Бернулли:
.
12. Дифференциальным
уравнением 2-го порядка называется
уравнение вида
![]() .
Если уравнение можно разрешить
относительно
.
Если уравнение можно разрешить
относительно
![]() ,
то его записывают в виде
,
то его записывают в виде
![]() .
.
13. Решением
дифференциального уравнения 2-го порядка
называется функция y = (x),
имеющая непрерывные производные
,
![]() на
некотором интервале (a; b)
и обращающая уравнение в верное числовое
равенство.
на
некотором интервале (a; b)
и обращающая уравнение в верное числовое
равенство.
14. Задача
Коши для
дифференциального уравнения 2-го порядка:
требуется найти решение y = (x)
уравнения, удовлетворяющее начальным
условиям y = y0,
![]() при x = x0.
при x = x0.
15. Общим
решением
дифференциального уравнения 2-го порядка
называется функция y = (x; С1; С2),
содержащая две произвольные постоянные
С1,
С2
и удовлетворяющая условиям: 1) при
любых начальных условиях
![]() система уравнений
система уравнений
 должна быть разрешима относительно
постоянных С1,
С2
так, что
должна быть разрешима относительно
постоянных С1,
С2
так, что
 2) при
всех значениях этих постоянных С1,
С2
функция y = (x; C1; C2)
обращает дифференциальное уравнение
в верное числовое равенство.
2) при
всех значениях этих постоянных С1,
С2
функция y = (x; C1; C2)
обращает дифференциальное уравнение
в верное числовое равенство.
16. Всякое решение, получаемое из общего при фиксированных значениях постоянных С1, С2 называется частным решением дифференциального уравнения.
17. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка:
а) ![]() решается повторным интегрированием.
решается повторным интегрированием.
б) ![]() ,
явно не содержащее искомой функции
,
явно не содержащее искомой функции
![]() .
Используется замена:
.
Используется замена:
![]() ,
где
,
где
![]() – новая неизвестная функция, тогда
– новая неизвестная функция, тогда
![]() .
Для нового уравнения относительно
функции p
находим общее решение и подставляем
его в формулу
.
Получаем ДУ с разделяющимися переменными
относительно функции y,
находим его общее решение.
.
Для нового уравнения относительно
функции p
находим общее решение и подставляем
его в формулу
.
Получаем ДУ с разделяющимися переменными
относительно функции y,
находим его общее решение.
в) ![]() ,
явно не содержащее независимой переменной
.
Замена:
,
где
,
явно не содержащее независимой переменной
.
Замена:
,
где
![]() ,
тогда
,
тогда
![]() .
Для нового уравнения относительно
функции p
находим общее решение и подставляем
его в формулу
.
Получаем ДУ с разделяющимися переменными
относительно функции y,
находим его общее решение.
.
Для нового уравнения относительно
функции p
находим общее решение и подставляем
его в формулу
.
Получаем ДУ с разделяющимися переменными
относительно функции y,
находим его общее решение.
18. Линейным
однородным дифференциальным уравнением
2-го порядка с постоянными коэффициентами
называется уравнение вида
![]() .
Составляется характеристическое
уравнение
.
Составляется характеристическое
уравнение
![]() .
.
Если
![]() ,
то
,
то
![]() и общее решение исходного уравнения
имеет вид:
и общее решение исходного уравнения
имеет вид:
![]() .
.
Если
![]() ,
то
,
то
![]() и
и
![]() .
.
Если
![]() ,
то
,
то
![]() и
и
![]() .
.
19. Линейным
неоднородным дифференциальным уравнением
2-го порядка с постоянными коэффициентами
с правой частью специального вида
называется уравнение вида
![]() .
Его общее решение ищется в виде
.
Его общее решение ищется в виде
![]() ,
где
,
где
![]() – общее решение соответствующего
линейного однородного дифференциального
уравнения 2-го порядка с постоянными
коэффициентами:
,
а
– общее решение соответствующего
линейного однородного дифференциального
уравнения 2-го порядка с постоянными
коэффициентами:
,
а
![]() – какое-либо частное решение исходного
уравнения.
– какое-либо частное решение исходного
уравнения.
Если
![]() ,
где
– некоторое число, Pn(x)
– многочлен степени n,
то
,
где
– некоторое число, Pn(x)
– многочлен степени n,
то
![]() ,
где
,
где
![]() – многочлен степени
– многочлен степени
![]() с неопределенными коэффициентами,
с неопределенными коэффициентами,
![]() – число, равное кратности
как корня характеристического уравнения
соответствующего линейного однородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами
.
– число, равное кратности
как корня характеристического уравнения
соответствующего линейного однородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами
.
Если
![]() ,
где ,
– некоторые числа, Pn(x),
Qm(x)
– многочлены степени n
и m
соответственно, то
,
где ,
– некоторые числа, Pn(x),
Qm(x)
– многочлены степени n
и m
соответственно, то
![]() ,
где
,
где
![]() – многочлены степени
– многочлены степени
![]() с неопределенными коэффициентами,
с неопределенными коэффициентами,
![]() ,
– число, равное кратности
,
– число, равное кратности
![]() как корня характеристического уравнения
соответствующего линейного однородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами
.
как корня характеристического уравнения
соответствующего линейного однородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами
.
