Числовые характеристики непрерывной случайной величины

17. Математическим ожиданием непрерывной случайной величины называется число .

18. Дисперсией называется число или .

19. Средним квадратическим отклонением называется число .

Законы распределения непрерывной случайной величины

20. Равномерное распределение: , , .

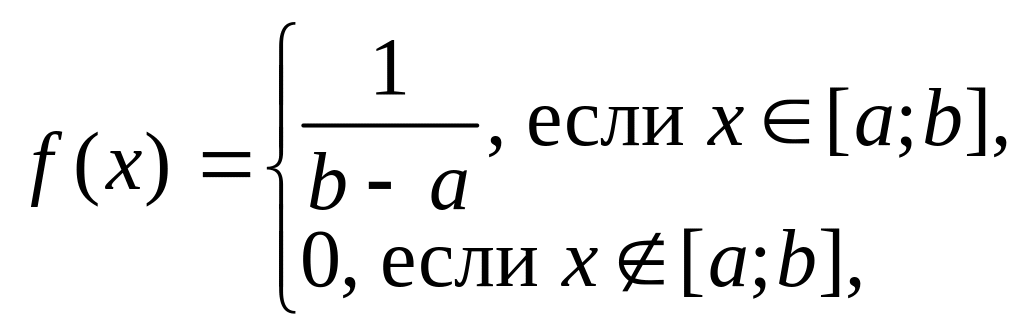
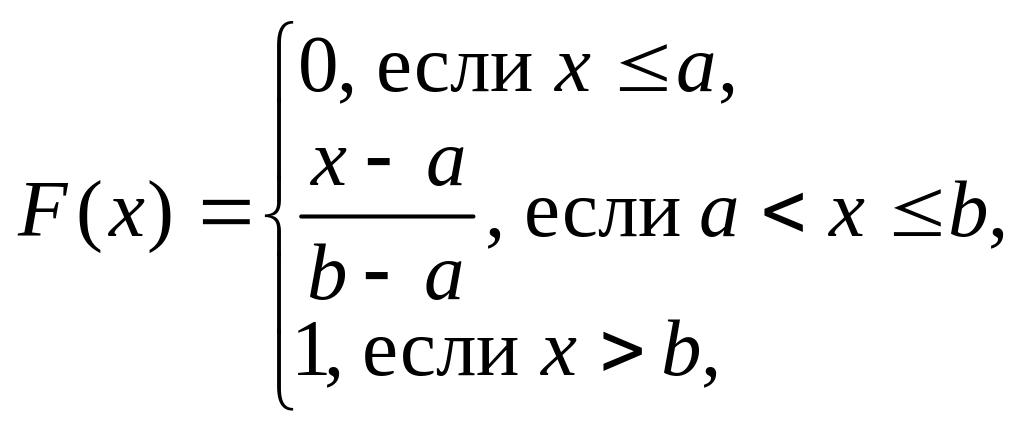
21. Показательное распределение: , .

22. Нормальное распределени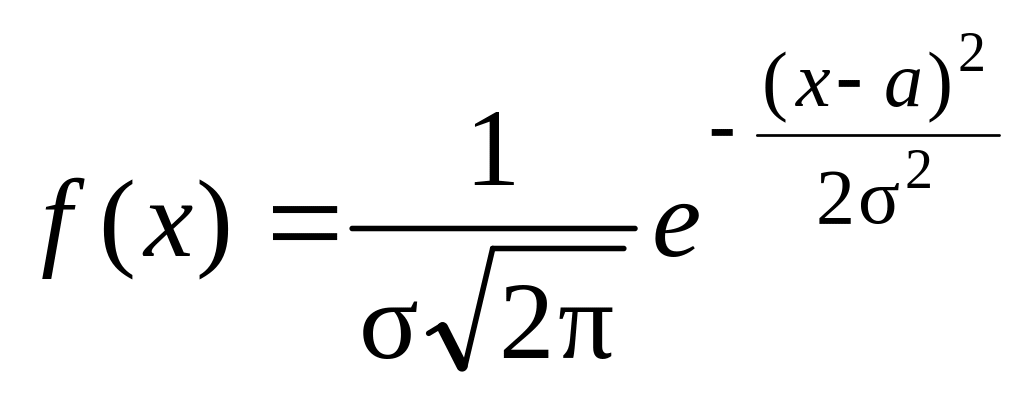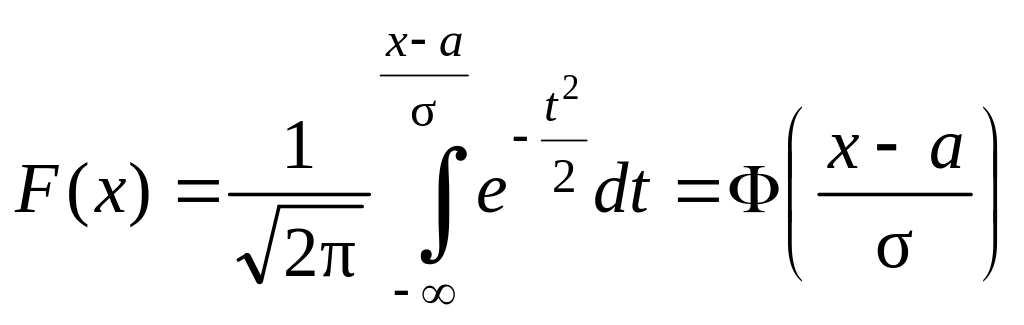е: , , где – функция Лапласа, , , .

5.3. Образец решения контрольной работы № 5.

Задание 1. На заочном отделении 80% всех студентов работают по специальности. Какова вероятность того, что из трёх отобранных случайным образом студентов по специальности работают: а) один; б) два; в) все; г) никто; д) хотя бы один студент?

Решение. Вероятность выбрать студента, работающего по специальности, равна p = 0,8, а вероятность выбрать неработающего студента равна q = 1 – p = 0,2. Так как отбирают 3 студентов, то n = 3.

а) Пусть событие А – «среди 3-х отобранных студентов только один работает по специальности», тогда вероятность этого события по формуле Бернулли равна .

б) По формуле Бернулли вероятность события В – «среди 3-х отобранных студентов два студента работают по специальности» равна .

в) Вероятность события С – «все трое отобранные студенты работают по специальности» равна .

г) Событие D – среди 3-х отобранных студентов никто не работает по специальности имеет вероятность .

д) Вероятность события Е – среди 3-х отобранных студентов работает по специальности хотя бы один студент вычислим по формуле , где противоположное событие – никто из 3-х отобранных студентов не работает по специальности. Так как (см. г)), то получим .

Ответ: а) 0,096; б) 0,384; в) 0,512; г) 0,008; д) 0,992.

Задание 2. Электролампы изготавливают на трех заводах. Первый завод производит 35 % общего количества электроламп, второй – 50 % и третий – 15 %. Продукция первого завода содержит 70 % стандартных ламп, второго – 80 % и третьего – 90 %. В магазин поступает продукция всех трех заводов. Какова вероятность того, что а) наудачу взятая лампа является стандартной; б) стандартная электролампа изготовлена на втором заводе?

Решение. Пусть событие А – купленная в магазине лампа является стандартной. Введем гипотезы: Н₁ – наудачу взятая лампа изготовлена на первом заводе, Н₂ – наудачу взятая лампа изготовлена на втором заводе и Н₃ – наудачу взятая лампа изготовлена на третьем заводе. Вероятности гипотез по условию равны: P(H₁)=0,35, P(H₂)=0,5 и P(H₃)=0,15. События Н₁, Н₂, Н₃ являются несовместимыми и образуют полную группу, сумма их вероятностей равна единице: 0,35+0,5+0,15=1. Из условия следует, что , и .

а) Согласно формулы полной вероятности, вероятность искомого события А равна .

б) Переоценим гипотезу Н₂ по формуле Байеса после того, как стало известно, что событие А произошло: .

Ответ: а) 0,78; б)  .

Задание 3. Каждый из трех клиентов, взявший кредит в банке, может вернуть его раньше срока с вероятностью 0,4. 1) Составить закон распределения дискретной случайной величины Х – числа клиентов, вернувших кредит в банк раньше срока; 2) построить многоугольник распределения вероятностей; 3) найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х.

Решение. Испытание состоит в попытке возвращения кредита раньше срока. В испытании может произойти или не произойти событие А – возвращение кредита раньше срока. Вероятность наступления события А равна P(A) = 0,4, тогда вероятность не наступления этого события равна q = 1 – 0,4 = 0,6. Рассматриваемая случайная величина Х в результате испытания может принять одно из следующих значений: 0, 1, 2 или 3.

Вероятности этих значений вычислим по формуле Бернулли:

;

;

;

.

1) Таким образом, случайная величина Х имеет следующий закон распределения вероятностей:

Х	0	1	2	3
Р	0,216	0,432	0,288	0,064

Контроль: 0,216 + 0,432 + 0,288 + 0,064 = 1.

2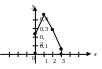 ) Строим многоугольник распределения вероятностей.

3) Определим математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х:

М(Х) = np = 30,4 = 1,2;

D(X) = npq = 30,40,6 = 0,72;

.

Ответ:	1)	Х	0	1	2	3	3)	M(X) = 1,2; D(X) = 0,72;
		Р	0,216	0,432	0,288	0,064

.

Задание 4. Непрерывная случайная величина X задана функцией распределения 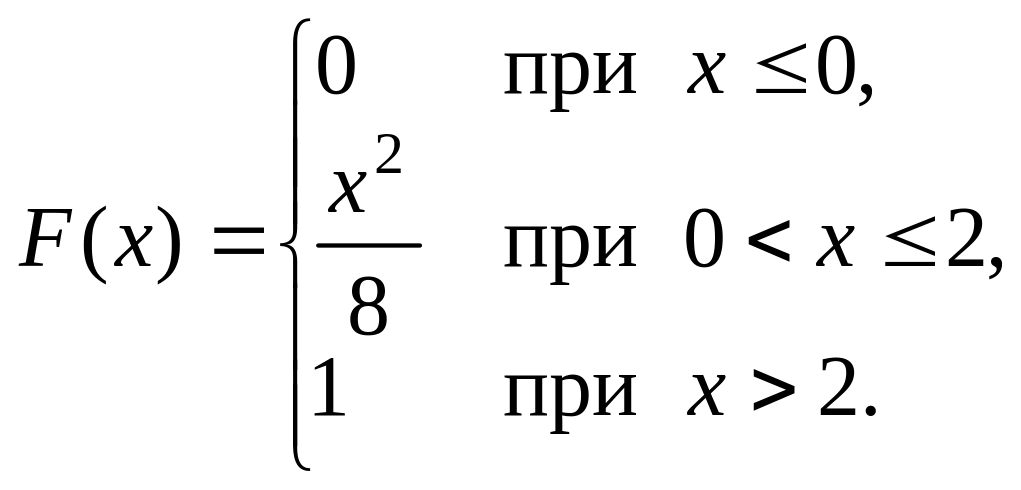Найти: 1) плотность распределения f(х); 2) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X; 3) построить графики функций F(x) и f(х).

Решение. 

1) Воспользуемся определением дифференциальной функции. При x  0 и при x > 2 имеем . При 0 < x  2 . Таким образом, величина Х имеет следующую дифференциальную функцию:

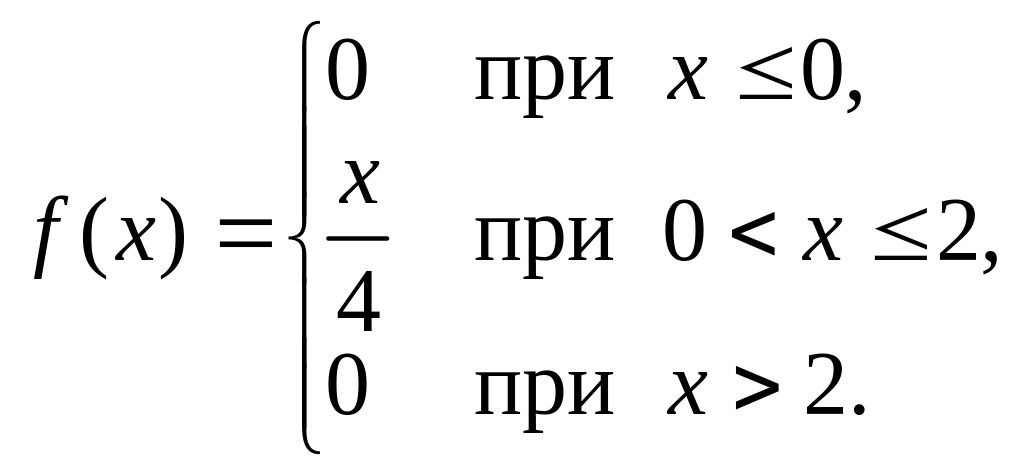
2) Найдем числовые характеристики случайной величины Х. Математическое ожидание равно: .

Дисперсия равна .

Среднее квадратическое отклонение равно .

3) Строим графики функций F(x) и f(х):

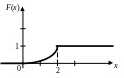
Ответ: 1) 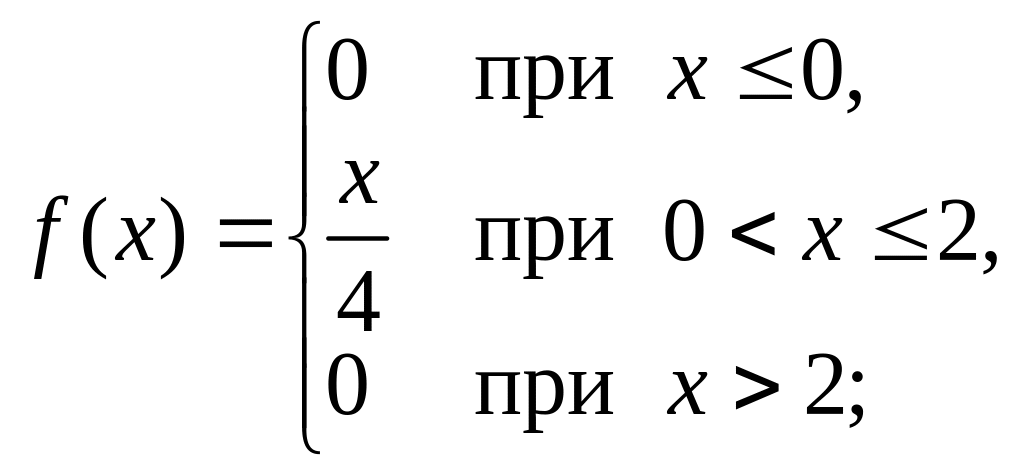 2)  , , .

5. Задана плотность распределения непрерывной случайной величины Х: Найти неизвестный параметр С.

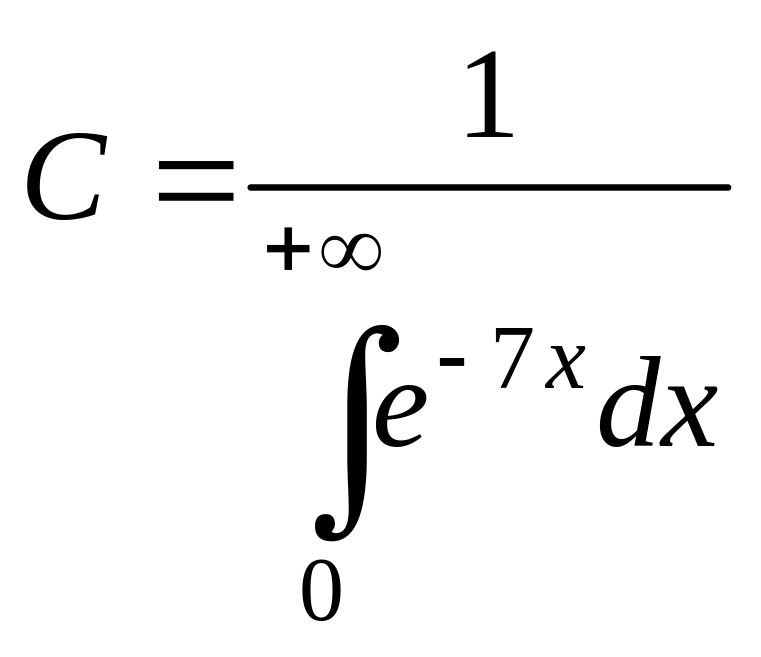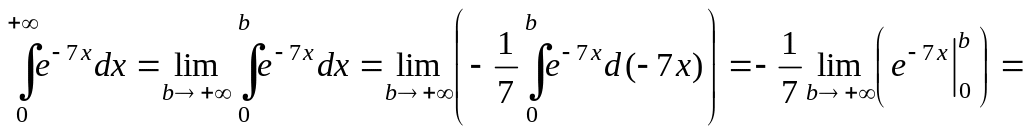
Решение. Для определения неизвестного коэффициента С воспользуемся свойством плотности распределения вероятности : , откуда . Так как , то .

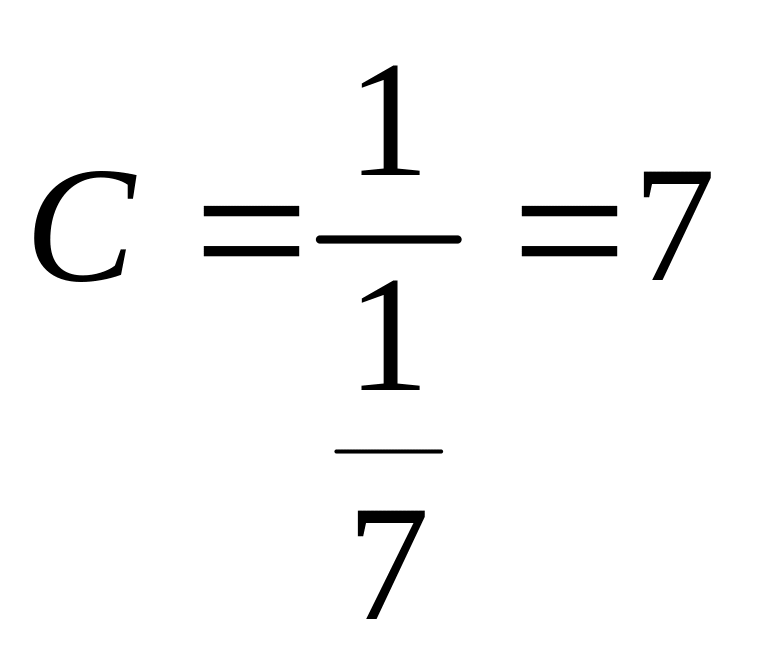Ответ: С = 7.