Приложения определенного интеграла в геометрии

5. Площадь криволинейной трапеции в декартовой прямоугольной системе координат (рис. 8) вычисляется по формуле: . Если на (график функции лежит ниже оси ), то .

6. Если криволинейная трапеция ограничена сверху кривой, заданной параметрически то площадь фигуры равна: , где и соответствуют значениям и .

7. Площадь криволинейного сектора, ограниченного кривой и двумя лучами и в полярных координатах (рис. 9) вычисляется по формуле: .

8. Если кривая задана уравнением в декартовой прямоугольной системе координат, то длина этой кривой от точки до точки вычисляется по формуле: . Если кривая определяется уравнением , то .

9. Если кривая задана параметрически , то длина кривой вычисляется по формуле: , где и соответствуют значениям и .

10. Если кривая задана уравнением в полярных координатах, то ее длина между лучами и равна: .

11. Объем тела, образованного вращением вокруг оси криволинейной трапеции (рис. 8), вычисляется по формуле: . Если эту криволинейную трапецию вращать вокруг оси , то объем тела вращения равен , причем .

12. Если криволинейная трапеция ограничена кривой ( ), осью и прямыми и (рис. 10), то объем полученного тела вращения вокруг оси равен: .

Рис. 10

13. Если дуга кривой, заданная в декартовых прямоугольных координатах , где , вращается вокруг оси , то площадь поверхности вращения вычисляется по формуле: .

14. Если дуга кривой , где вращается вокруг оси , то площадь поверхности вращения вычисляется по формуле: .

15. Если дуга кривой задана параметрически где , то площадь поверхности вращения вокруг оси равна: .

16. Если дуга задана в полярных координатах , где , то .

3.3. Образец решения контрольной работы № 3.

Задание 1. Найти неопределенные интегралы. Результаты проверить дифференцированием.

1)  ; 2)  ;

3)  ; 4)  .

Решение. 1) Интеграл преобразуем к табличному методом замены переменной. Так как , то, вводя новую переменную находим интеграл:

.

Проверка. Покажем, что производная от найденного неопределённого интеграла равна подынтегральной функции. По свойству неопределённого интеграла это означает, что интеграл найден верно.

. Интеграл найден верно.

2) Преобразуем интеграл к виду :

. Учитывая, что

, то после введения новой переменной получаем табличный интеграл:

.

Проверка.

. Интеграл найден верно.

3) Для интегрирования произведения степенной функции на трансцендентную функцию (тригонометрическую, обратно тригонометрическую, показательную или логарифмическую) применяется метод интегрирования по частям, опирающийся на использование формулу интегрирования по частям . (*)

Пусть и , тогда и .

Применяя формулу (*), находим:

.

Проверка.

. Интеграл найден верно.

4) Для нахождения неопределённого интеграла от неправильной рациональной дроби, степень числителя которой больше или равна степени знаменателя, выделим из дроби целый многочлен и правильную дробь, используя деление многочленов «уголком»:

Таким образом, имеем:

Следовательно, по свойству неопределённого интеграла

(*)

В последнем интеграле квадратный трёхчлен имеет два действительных корня, которые находим из квадратного уравнения :

После этого правильная рациональная дробь может быть разложена на сумму двух простейших элементарных дробей методом неопределённых (буквенных) коэффициентов следующим образом:

(**), где А и В – неопределённые коэффициенты.

Приводя к общему знаменателю сумму и группируя по степеням переменной х, получаем:

.

Из равенства (**) следует, что , а это возможно тогда и только тогда, когда или Решая систему двух линейных уравнений с двумя неизвестными, находим неопределенные коэффициенты: , .

Подставим найденные значения А и В в равенство (**), получим:

Следовательно,

Исходный интеграл в формуле (*) примет вид:

.

Проверка.

. Интеграл найден верно.

Ответ: 1)  ; 2)  ; 3)  ; 4)  .

Задание 2. Вычислить по формуле Ньютона-Лейбница определенный интеграл .

Решение. Формула Ньютона – Лейбница имеет вид:

Для вычисления заданного интеграла используем метод замены переменной в определённом интеграле: , , .

Найдём пределы интегрирования для новой переменной t. Если , то . Если , то . Итак, Вычисляем интеграл, переходя к новой переменной с новыми пределами интегрирования:

Ответ:  .

Задание 3. Вычислить площадь фигуры, ограниченной графиками функций и . Сделать чертеж.

Решение. Для выполнения чертежа (рисунка фигуры) найдём координаты вершины параболы и точек пересечения параболы с прямой. Вершина параболы находится в точке экстремума функции Поэтому найдём производную и приравняем её нулю.

По уравнению параболы находим Вершина параболы находится в точке , ветви параболы направлены вниз.

Для нахождения точек пересечения параболы и прямой необходимо решить систему двух уравнений:

Точками пересечения являются и Делаем чертёж фигуры.

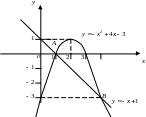
Для вычисления площади S полученной фигуры будем использовать формулу: , где – уравнение кривой, которая ограничивает фигуру сверху, а – уравнение кривой, ограничивающей фигуру снизу, и – абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае: , , и .

Вычисляем площадь фигуры:

(кв. ед.).

Ответ: 4,5 (кв. ед.).

Задание 4. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной графиками функций и .

Решение. Для выполнения чертежа фигуры найдём координаты точек пересечения параболы с прямой, решив систему двух уравнений:

Точками пересечения являются и . Делаем чертёж фигуры.

Для вычисления объема V, получаемого при вращении данной фигуры вокруг оси Ох, будем использовать формулу: , где – уравнение кривой, которая ограничивает фигуру сверху, а – уравнение кривой, ограничивающей фигуру снизу, и – абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае: , , и .

Вычисляем объем:

(куб. ед.).

Ответ:   (куб. ед.).