
- •Практичне заняття № 1
- •Хід заняття
- •І. Розв’язування вправ
- •Іі Завдання додому
- •Практичне заняття № 2
- •Хід заняття
- •І Розв’язування вправ
- •Iі Завдання додому
- •Практичне заняття № 3
- •Хід заняття
- •І. Розв’язування вправ.
- •Іі. Завдання додому.
- •1. Лінійна модель міжнародної торгівлі.
- •Практичне заняття № 4
- •Хід заняття
- •І Розв’язування вправ.
- •Iі Завдання додому
- •Практичне заняття № 5
- •Хід заняття
- •І Розв’язування вправ
- •Додатково:
- •Iі Завдання додому
- •Практичне заняття № 6 Тема: Обчислення рангу матриці. Теорема Кронекера - Капеллі
- •Хід заняття
- •І Розв’язування вправ.
- •Іi Завдання додому
- •Практичне заняття № 7
- •Хід заняття
- •І Розв’язування вправ
- •Iі Завдання додому
- •Практичне заняття № 8
- •Хід заняття
- •І Розв’язування вправ
- •Iі Завдання додому
- •Практичне заняття № 9
- •Хід заняття
- •І Розв’язування вправ
- •Iі Завдання додому
- •Практичне заняття № 10
- •Хід заняття
- •І. Актуалізація опорних знань студентів
- •Іі. Розв’язування вправ
- •Ііі Підведення підсумку заняття іv. Завдання додому
- •Практичне заняття № 11
- •Хід заняття
- •І Розв’язування вправ
- •Iі Завдання додому
- •Практичне заняття № 12
- •Хід заняття
- •І Розв’язування вправ
- •Iі Завдання додому
- •Практичне заняття № 13
- •Хід заняття
- •І Розв’язування вправ
- •II Завдання додому
- •Ііі. Підведення підсумків заняття іv. Завдання додому
- •Іі Доповнення до лекції “Частинні похідні вищого порядку”
- •Іiі Розв’язування вправ
- •Іv Завдання додому
- •Практичне заняття № 16
- •Хід заняття і. Розв`язування вправ
- •Практичне заняття № 17
- •Хід заняття
- •І Актуалізація опорних знань (фронтальне опитування).
- •Іі Розв’язування вправ.
- •Ііі Підведення підсумків заняття
- •IV Завдання додому
- •Практичне заняття № 18
- •Хід заняття
- •Правило позначення через “u” I “dv”
- •І Розв’язування вправ.
- •Iі Завдання додому
- •Практичне заняття № 19
- •Хід заняття
- •Хід заняття
- •І. Розв’язування вправ
- •Iі. Завдання додому
- •Практичне заняття № 21
- •Хід заняття і Розв’язування вправ
- •Іi Завдання додому
- •Практичне заняття № 22
- •Хід заняття
- •І. Розв’язування вправ
- •Iі. Завдання додому
- •Іiі Завдання додому
- •Іі Розв’язування вправ
- •Ііi Завдання додому
- •Іiі Завдання додому
- •Практичне заняття № 30
- •Хід заняття
- •І Розв’язування прав.
- •Iі Завдання додому
- •Задачі економічного змісту
І. Розв’язування вправ.
1) Знайти власні числа і власні вектори лінійних операторів, заданих матрицями:
а)
![]() б).
б).

Відповідь: Відповідь:


2)
Квадратичну форму
![]() записати в матричному вигляді.
записати в матричному вигляді.
Відповідь:

Знайти
 в
базисі
в
базисі
 ,
якщо
,
якщо
а)![]() ,
,
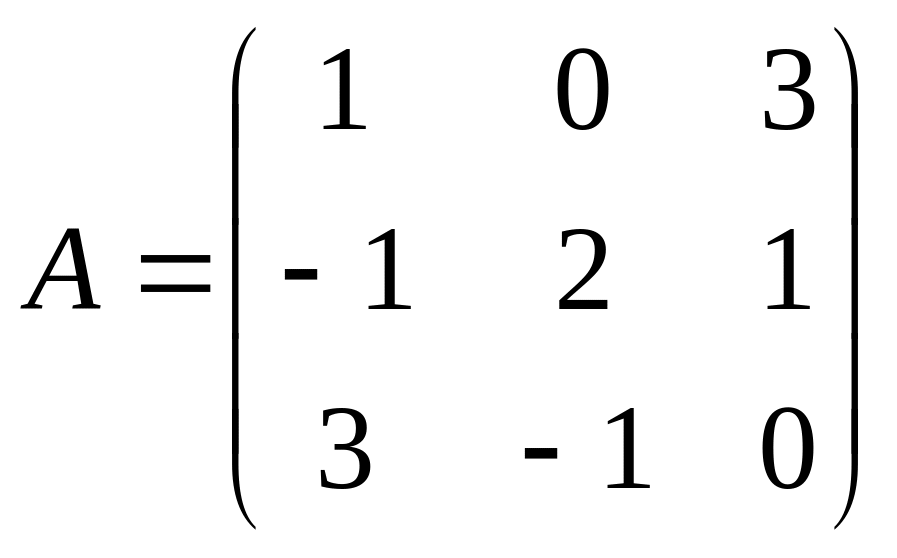
б)
![]() ,
,

Знайти власні числа і власні вектори лінійного оператора заданого матрицею.
а)
![]()
б)
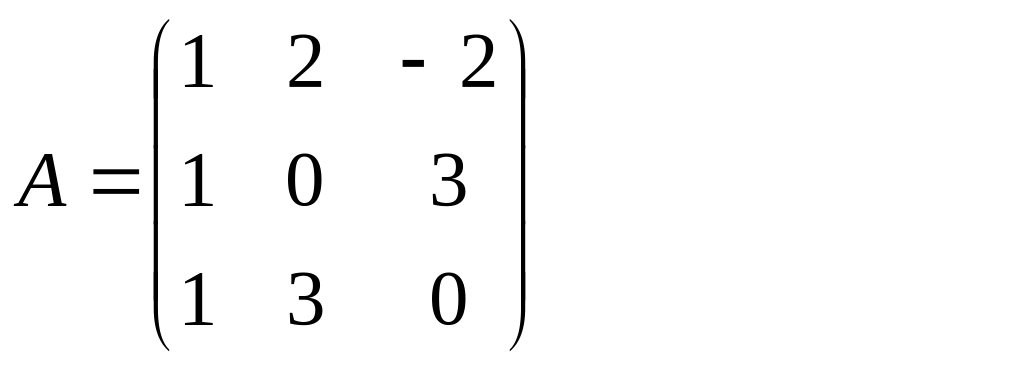
Записати в матричному вигляді квадратичну форму.
![]()
Задано квадратичну форму
 .
Знайти
.
Знайти
квадратичну
форму, що отримали із заданої лінійним
перетворенням
![]()
Квадратичну форму
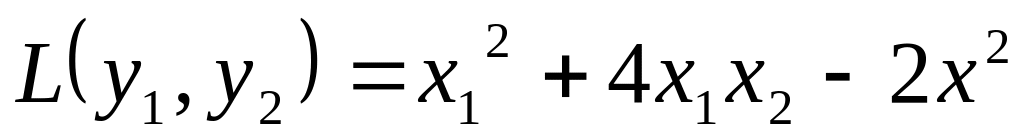 привести до канонічного
привести до канонічного
виду.
Іі. Завдання додому.
1. Лінійна модель міжнародної торгівлі.
Розглянемо торгівлю між n країнами. Їх торгівельні бюджети х1, х2,…, хn використовуються на закупівлю товарів. Нехай аіj – доля бюджету хj (j - країни) використана на закупівлю товарів у і – країни. Вважаємо, що весь бюджет j – країни використовується на закупівлю товарів як у межах країни, так і поза неї, тобто
![]() (j
=
1,2,…, n)
(j
=
1,2,…, n)
Матрицю
А =
![]() називають структурною матрицею, тому
що сума чисел в кожному стовбці дорівнює
одиниці.
називають структурною матрицею, тому
що сума чисел в кожному стовбці дорівнює
одиниці.
Умова збалансованої (бездефіцитної) торгівлі:
![]()
![]() А
А![]()
Нехай структурна матриця торгівлі для трьох країн А має вигляд
А =
 ,
,
а консолідований торговельний бюджет дорівнює х1+ х2+ х3 = 1200 у.о.
Знайти граничний розподіл торгівельних бюджетів цих країн, стан якого визначається власним вектором цієї матриці.
Повторити лекції «Визначники», «Матриці та дії з ними».
Відповідь: х1 = 400 у.о., х2 = 200 у.о., х3 = 600 у.о.
Практичне заняття № 4
Тема: Розв’язування систем лінійних рівнянь за допомогою формул Крамера
Мета: сформувати вміння та навики розв’язування систем лінійних рівнянь за
допомогою формул Крамера
Хід заняття
Системою лінійних рівнянь з невідомими називають систему, яка має вигляд
![]()
![]() ;
;
![]() , (1)
, (1)
де
![]() -
матриця розміром
на
з компонентами
-
матриця розміром
на
з компонентами
![]() ,
,
![]() - вектор-стовбець, компонентами якого
являються
- вектор-стовбець, компонентами якого
являються
![]() невідомих,
невідомих,
![]() - вектор вільних членів.
- вектор вільних членів.
За
формулами Крамера розв’язок системи
єдиний при
![]() та має вигляд
та має вигляд
![]() ,
,
де
![]() є визначник, який формується з
є визначник, який формується з
![]() заміною
стовпця на стовпець-вектор
заміною
стовпця на стовпець-вектор
![]()
![]() .
.
Формули Крамера для системи трьох лінійних рівнянь з трьома невідомими:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
І Розв’язування вправ.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8) За умовою задачі скласти систему лінійних рівнянь та розв’язати методом Крамера:
Підприємство спеціалізується на виробництві продукції трьох видів Х1, Х2, Х3 і використовує сировину трьох типів S1, S2, S3. Норми витрат кожної з них на одну одиницю виробу та обсяг витрат сировини на один день задані таблицею:
Вид сировини |
Норми витрат сировини на одиницю виробу (ум.од) |
Витрати сировини на один день (ум.од) |
||
1-й вид |
2-й вид |
3-й вид |
||
S1 |
3 |
5 |
4 |
2700 |
S2 |
2 |
1 |
6 |
1600 |
S3 |
5 |
2 |
2 |
1900 |
Визначити щоденний обсяг випуску кожного виду виробу.
