І Розв’язування вправ

1) Знайти матрицю -3А+4В, якщо

,

2) Знайти добуток матриць АВ і ВА , якщо

,

3) Знайти добуток матриць:

4) Знайти приєднану матрицю:

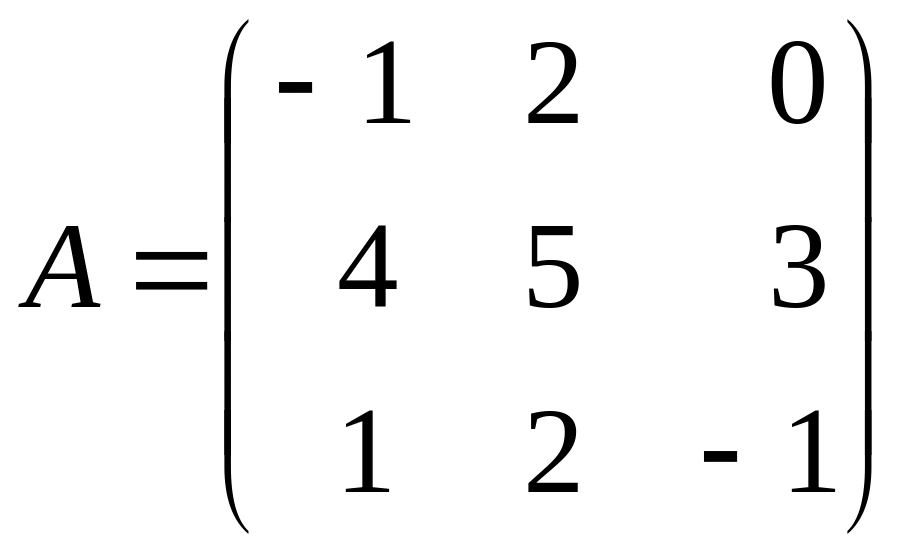
5) Додатково:

а)

б)

Iі Завдання додому

Виконати дії:

1) 3

2)

3)

4)

5) Знайти АВС:

6) Знайти D=ABC-3E:

7) Підприємство виготовляє чотири види виробів з використанням чотирьох видів сировини. Норма споживання сировини задана матрицею (сировина у кг):

Види сировини:

1 2 3 4

1 2 3 4

Види виробу

Знайти затрати сировини кожного виду при заданому плані випуску виробів відповідно 50, 40, 30, 25.

8) Нехай підприємство випускає 3 вироби, кожний з яких виготовляється з 3 видів сировини.

Таблиця Аmn включає у себе по рядках: m=1 - значення вартості однієї одиниці сировини з 3-х елементів – стовбців, відповідних видам сировини, а ; m=2 – собівартість переробки однієї одиниці сировини з трьома відповідними елементами - а ; m=3 – прибуток з використання одиниці сировини з трьома відповідними елементами - а :

А33 =

До другої таблиці В по стовбцях входять по з елементи, що дорівнюють кількості одиниць сировини кожного з з-х видів, які входять до складу кожного з з-х виробів відповідно - В (n= 1,2,3 –вид сировини, к= 1,2,3 – різновиду виробу).

Третя таблиця Сmk являється добутком перших двох: Аmn В = Сmk:

Сmk: = , де

елементами рядків є сумарна вартість сировини з-х видів, собівартість її переробки, прибуток від її реалізації для кожного з трьох різновидів виробів відповідно.

Знайти матрицю В .

Відповіді:

1)

2) ( -3 8 11 11)

3)

4) Е=

5)

6)

7) 550 кг, 245 кг, 420 кг, 545 кг.

8) В =

Практичне заняття № 3

Тема: Власні числа і власні вектори матриці. Квадратичні форми

Мета: формувати навички знаходження власних чисел і власних векторів матриці, вміння квадратичні форми записувати в матричному виді.

Хід заняття

Ненульовий вектор називається власним вектором лінійного оператора , якщо знайдеться таке число , що . Число називається власним числом або власним значенням оператора , відповідним вектору .

Власні числа оператора , якому відповідає матриця , знаходяться з матричного рівняння:

,

Нетривіальні значення для знаходимо з умови , тобто визначник матриці однорідної системи дорівнює нулю.

- характеристичне рівняння оператора (або матриці А).

Розв’язавши рівняння, знайдемо , і, підставивши в систему, знайдемо координати власного вектора.

Квадратичною формою від n змінних називається сума, кожний член якої є квадратом однієї із змінних або добутком двох різних змінних з деяким коефіцієнтом.

…