Глава 3. Смеси веществ

3.1. Способы задания состава смеси. Закон Амага.

Для проведения термодинамических расчетов систем с газовыми смесями или растворами необходимо знать их состав. Состав смеси может быть задан:

- массовыми долями , где- молярная массаi-го компонента, кг/моль;M_i– относительная молекулярная массаi-го компонента;n_i– количествоi-го вещества, моль;

для каждой фазы ;

- молярными долями , где- количество вещества смеси, моль; для каждой фазы сумма молярных долей компонентов смеси;

- объемными долями, которые равны молярным долям , где- объемi-го компонента смеси, который при температуре и давлении смеси газов называется приведенным объемом;, м³/моль – молярный объемi-го компонента смеси. В соответствии с законом Авагадро молярные объемы всех компонентов смеси газов равны и, где. Сумма приведенных объемов компонентов смеси газов равна объему смеси (закон Амага), т.е..

Состав смеси идеальных газов может быть также задан парциальными давлениями р_i, массовыми концентрациямии молярными концентрациями.

При задании состава растворов пользуются массовыми и молярными концентрациями.

Парциальное давление р_i – это давлениеi-го компонента газовой смеси при условии, что он занимает весь объем, предназначенный для смеси, при температуре смеси.

3.2. Соотношения для смесей идеальных газов. Закон Дальтона

Средняя молярная масса смеси газов определяется выражением , кг/моль, где- масса смеси;- количество вещества смеси. Тогда

.

Удельная газовая постоянная смеси газов

, Дж/(кгК),

где Дж/(мольК) – молярная газовая постоянная;- молярная масса смеси.

Закон Дальтона:

, Па,

т.е. сумма парциальных давлений отдельных газов, входящих в смесь, равна полному давлению смеси. Таким образом, каждый газ в сосуде занимает весь объем при температуре смеси, находясь под собственным парциальным давлением.

Уравнение состояния для смеси идеальных газов имеет вид:

.

Для парциального давления и для приведенного объема i-го компонента смеси уравнения состояния имеют вид:

Тогда, разделив эти уравнения почленно первое на второе, имеем

.

Разделив уравнение на уравнениепочленно, получим:

.

Глава 4. Теплоемкость

4.1. Виды теплоемкости

Теплоемкость – это свойство тел поглощать и выделять теплоту при изменении температуры на один градус в различных термодинамических процессах. Различают общую среднюю и общую истинную теплоемкости.

Общая средняя теплоемкость термодинамического процесса (ТП) – это теплоемкость тела массой m, кг за конечный отрезок ТП:

,[Дж/К].

Общая истинная теплоемкость ТП – это теплоемкость тела массой m, кг в каждый данный момент ТП:

, [Дж/К].

Рассмотрим произвольный ТП 1-2 в координатах , гдеQ– подведенная теплота в [Дж];t – температура в [⁰C]. Тогда,.

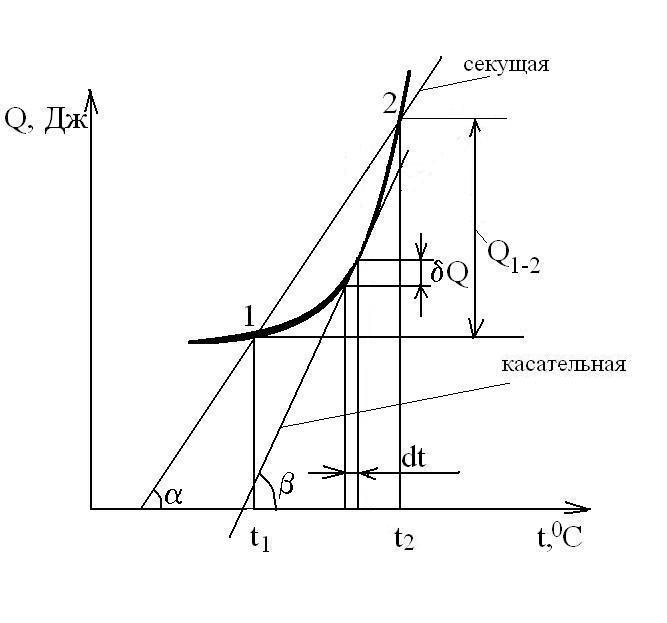
Если ТС – однородное рабочее тело, то в расчетах применяются относительные теплоемкости:

- удельная теплоемкость – теплоемкость, отнесенная к 1 кг вещества с=С/m, Дж/кгК;

- молярная теплоемкость – теплоемкость, отнесенная с 1 молю вещества , Дж/мольК;

- объемная теплоемкость – теплоемкость, отнесенная к 1м³вещества, Дж/м³К.

Теплоемкость – функция процесса и зависит от рода рабочего тела, характера процесса и параметров состояния. Так, теплоемкость в процессе с постоянным давлением называется изобарной теплоемкостью:

,

где H, Дж – энтальпия.

Теплоемкость в процессе с постоянным объемом называется изохорной теплоемкостью:

,

где U, Дж – внутренняя энергия.

Теплоемкость идеального газа не зависит от температуры и давления и зависит только от числа степеней свободы движения молекул и в соответствии с законом о равном распределении энергии по степеням свободы движения молекул теплоемкость: , где- вращательные степени свободы, равные для одноатомного газа нулю, для двухатомного газа -=2 и для трехатомных газов=3;Дж/мольК – молярная газовая постоянная. Теплоемкостьопределяется по уравнению Майера:

.

Для одноатомного газа и, для двухатомного газаи, для трех и более атомных газови.

Теплоемкость реальных газов зависит от давления и температуры. В ряде случаев можно пренебречь влиянием давления на теплоемкость и принять, что теплоемкость реальных газов зависит только от температуры: C=f(t). Эта зависимость определяется экспериментально.

Эмпирическая зависимость удельной истинной теплоемкости от температуры может быть представлена в виде многочлена:

, Дж/кгК,

где при температуреt=0⁰C. Для двухатомных газов можно ограничиться двумя слагаемыми:, или, где.

Для конечного участка процесса 1-2 количество теплоты равно:

.

Тогда средняя теплоемкость на этом участке процесса будет равна:

, Дж/кгК.

В области низких температур при Т<100К прекращается вращательное движение молекул и колебательное движение атомов, а при температуреТ→0К прекращается и поступательное движение молекул, т.е. приТ=0КС_р=C_v=0 и прекращается тепловое движение молекул (опытные данные Нернста и др., 1906-1912гг.). При температуреТ→0К свойства веществ перестают зависеть от температуры, как это иллюстрируется на приведенном графике зависимости теплоемкости от абсолютной температуры.