7.2. Характеристические функции и дифференциальные соотношения взаимности термодинамики

Характеристической функцией называется функция состояния ТС, позволяющая при соответствующем выборе независимых переменных (при определенных условиях сопряжения ТС с окружающей средой) выражать через свои производные наиболее просто и в явном виде термодинамические параметры, характеризующие свойства термодинамической системы. Построение термодинамического анализа на этих свойствах характеристических функций составляет основу метода характеристических функций.

Рассмотрим простую (ℒ=0), закрытую () термодинамическую систему. Тогда для обратимых процессов объединенные выражения 1-го и 2-го законов термодинамики будут иметь вид:

, (5)

(6)

(7)

. (8)

Каждое из уравнений (5)-(8) связывает пять переменных величин, которые зависят лишь от состояния ТС и не зависят от пути процесса. Функции U, H, F, Gявляются характеристическими только при определенном выборе независимых переменных:. Полные дифференциалы функцийU, H, F, Gимеют вид:

(9)

(10)

, (11)

. (12)

Линейным дифференциальным соотношениям (9)-(12) тождественны объединенные выражения 1-го и 2-го законов термодинамики (5)-(8). Сопоставляя уравнения (5) и (9) можно наиболее просто выразить неизвестные параметры – температуру Ти давлениер с помощью частных производных внутренней энергии по энтропииSи по объемуV:

,. (13)

По аналогии выразим неизвестные параметры в выражениях (6)-(8) с помощью частных производных (10)-(12) для функций H, FиG:

,, (14)

,, (15)

,. (16)

Согласно свойству полного дифференциала вторая смешанная производная от функции Uне зависит от порядка дифференцирования, т.е.:

, или (17)

.

По аналогии для функций H, F,Gполучим:

, дляН, (18)

, дляF, (19)

, дляG. (20)

Уравнения (17)-(20) называются дифференциальными соотношениями взаимности или уравнениями Максвелла. Они в такой же степени достоверны, как и законы термодинамики, следствием которых они являются. Уравнения (17)-(20) широко используются при термодинамическом анализе. При анализе также широко используется уравнение связи, которое выводится следующим образом. Если функция - функция состояния, то ее полный дифференциал равен:

.

Для =const. Тогда получим:

.

После деления на имеем:

. (21)

Связи частных производных одного термодинамического параметра по другому (21) справедливы при определенных условиях сопряжения ТС с окружающей средой.

Схема чередования термодинамических параметров в уравнении связи (21) имеет вид:

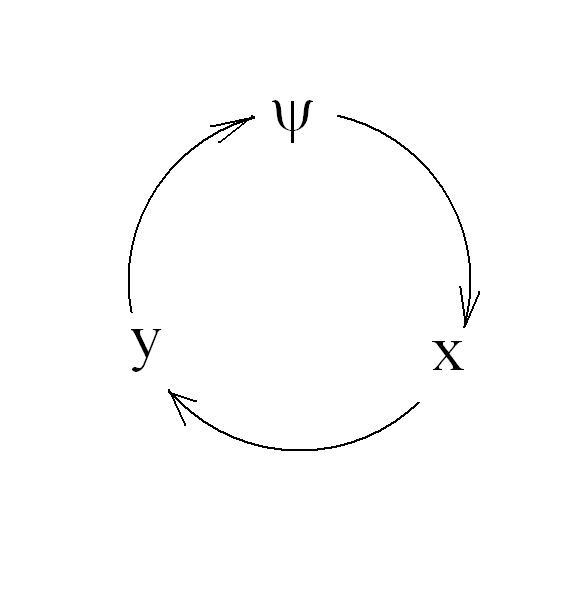
т.е. функция → аргумент → фиксированный параметр: (), (), ().

7.3. Максимальная и минимальная работы процесса. Термодинамические потенциалы

По изменению характеристических функций можно определить максимальную работу немеханического характера при соответствующих условиях сопряжения ТС с окружающей средой, т.е. при двух фиксированных независимых параметрах. Так, для сложной закрытой ТС, в которой протекают процессы с двумя фиксированными параметрами, находящимися под знаками дифференцирования в правых частях объединенных выражений 1-го и 2-го законов термодинамики (1)-(4) получим следующие соотношения:

при S, V=const ℒ_s,V , (22)

при S, p=const ℒ_s,p , (23)

при T, V=const ℒ_T,V, (24)

при T, p=const ℒ_T,p, (25)

где ℒ=- сумма работ немеханического характера. Для конечного процесса 1-2 эти выражения запишем в виде, умножив левые и правые части уравнений (22)-(25) на минус единицу (-1). Тогда:

ℒ_s,V, (26)

ℒ_s,p, (27)

ℒ_T,V, (28)

ℒ_T,p, (29)

При протекании обратимых процессов работа немеханического характера ℒ максимальна и равна уменьшению соответствующей характеристической функции, т.е.:

ℒ_{s,V max},

ℒ_{s,p max},

(30)

ℒ_{T,V max},

ℒ_{T,p max}.

При протекании необратимых процессов с максимальными потерями работоспособности ТС работа немеханического характера равна нулю, т.е.

ℒ_min=0. (31)

В общем случае при необратимых процессах часть энергии упорядоченного движения материи диссипирует (рассеивается) в энергию теплового неупорядоченного движения и работа немеханического характера ТС ℒ будет меньше максимальной работы в обратимых процессах.

В термодинамике характеристические функции: U, H, F, G, дифференциалы которых с обратным знаком равны элементарной работе немеханического характера, называют термодинамическими потенциалами:

U– изохорно-изоэнтропийный потенциал,

H– изобарно-изоэнтропийный потенциал,

F– изохорно-изотермический потенциал,

G – изобарно-изотермический потенциал.

Уменьшение термодинамических потенциалов при фиксации двух параметров в обратимых процессах равно максимальной работе ТС.

Таким образом, сумма работ немеханического характера может быть определена через изменения характеристических функций при фиксации двух независимых параметров.