7.5. Связь между изобарной и изохорной теплоемкостями в общем виде

Функция состояния ТС – энтропия может быть представлена в виде функциональной связи S=S(T,V). Дифференциал энтропии – полный дифференциал, т.е.

. (1)

Разделим уравнение (1) на dTи умножим наТприр=const. Тогда имеем:

. (2)

По определению и. После их подстановки в (2) получим:

. (3)

Производная включает калорическую величину – энтропию и неудобна при расчетах. Поэтому заменим эту производную, используя соотношения взаимности Максвелла для смешанных производных от свободной энергии Гельмгольца:

.

Тогда, используя уравнение связи в виде:

, получим:

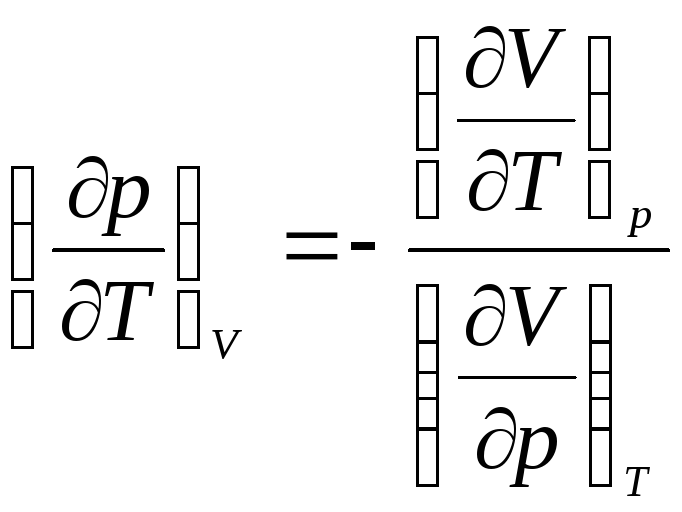. (4)

Подставим выражение (4) вместо в (3) и получим:

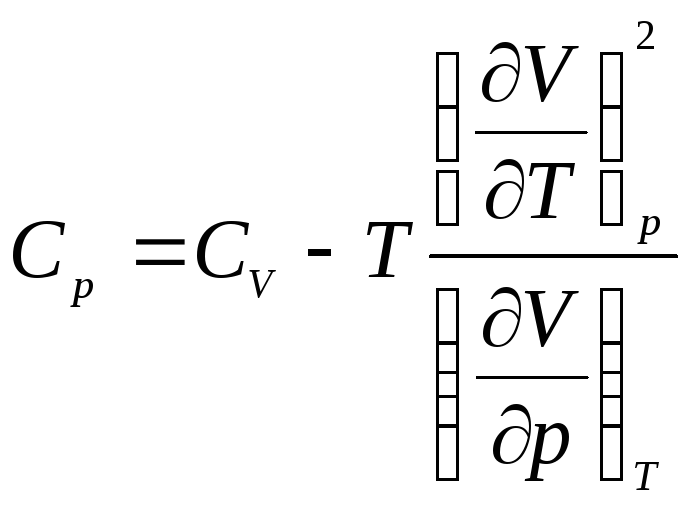. (5)

Покажем, как из уравнения (5) можно получить уравнение Майера для идеального газа, дифференцируя уравнение состояния:

. Тогдаи.

После подстановки этих производных в (5) получим:

, Дж/К.

Таким образом, получили уравнение Майера для общих теплоемкостей С_р и С_Vсистемы:

.

Получим связь между С_риC_Vв другом виде, используя производные от натуральных логарифмов параметров и учитывая, что.

Тогда получим, что

и. (6)

После подстановки выражений (6) в уравнение (5) с учетом, что , окончательно получим связь между изобарной и изохорной теплоемкостями в общем виде:

.

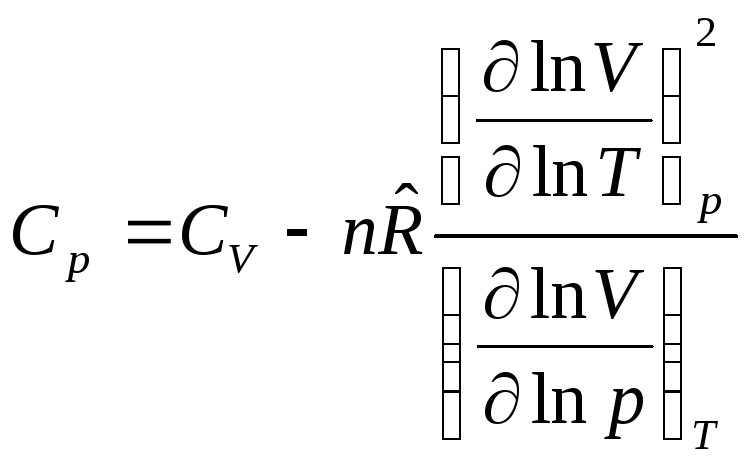7.6.Расчетные выражения для скорости звука в общем виде

По определению адиабатная скорость звука равна:

, (1)

где плотность газа и. Тогда:

. (2)

По уравнению связи частных производных одного параметра по другому имеем:

, откуда:

.

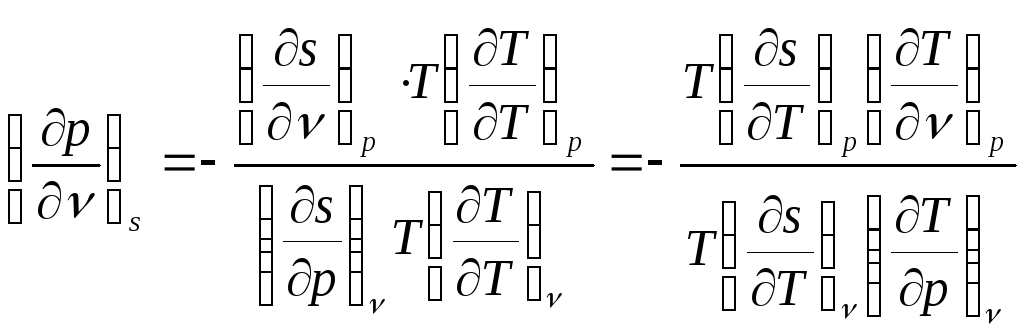По определению изобарная и изохорная удельные теплоемкости равны:

и. Тогда

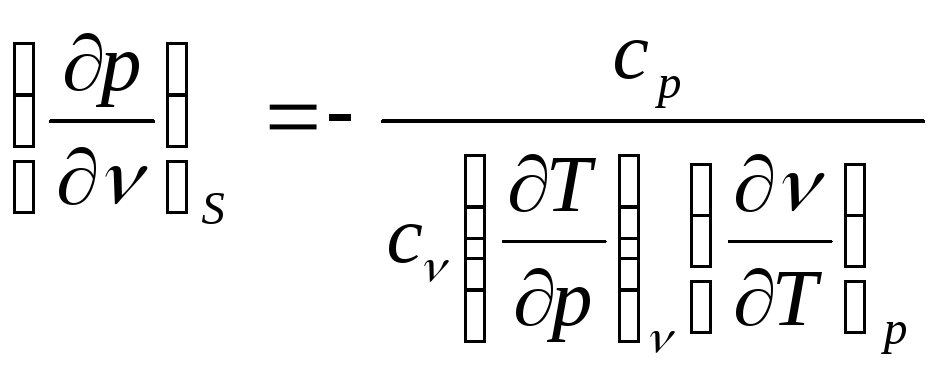. (3)

После подстановки выражения (3) в (2) имеем:

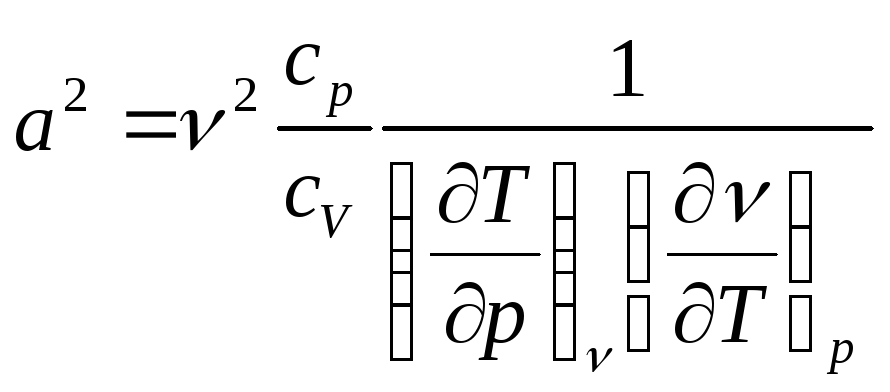. (4)

По уравнению связи:

, имеем:

. (5)

После подстановки выражения (5) в (4) окончательно имеем выражение для расчета скорости звука в общем виде:

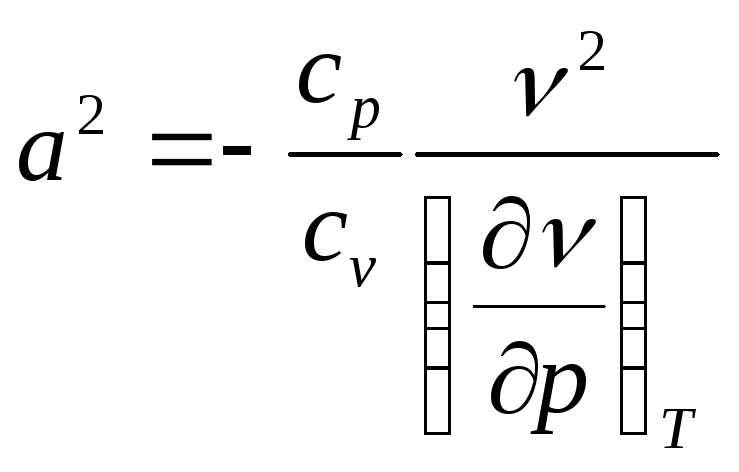. (6)

Из формулы (6) получим формулу для расчета скорости звука в идеальном газе при условии, что удельная газовая постоянная Rне зависит от давления и температуры. Тогда из уравнения состояния для 1 кг идеального газа:, имееми производную. После подстановки выражения дляв формулу (6) получим:

, где- показатель адиабаты,. Тогда:- скорость звука в идеальном газе.

7.7. Максимальная и минимальная теплоты процесса

Уравнения первого закона термодинамики в сложных закрытых ТС при двух фиксированных параметрах имеют вид:

- для изохорно-изотермического процесса (T,V=const):ℒ_Т,V ;

- для изобарно-изотермического процесса (T,p=const): ℒ_Т,р.

При написании этих уравнений использовалось правило знаков, принятое в термодинамике, т.е. , если теплота подводится к ТС, иℒ>0, если работа совершается термодинамической системой. В термохимии принято противоположное правило знаков для теплоты, т.е. теплота, (положительна), если она отводится от ТС. Тогда для конечных процессов 1-2 уравнение 1-го закона термодинамики будет иметь вид:

ℒ_Т,V, (1)

ℒ_Т,р, (2)

Соотношения (1) и (2) справедливы для любых процессов, обратимых и необратимых.

Для обратимого процесса ℒ=ℒ_max , :

ℒ_{Т,V max}, (3)

ℒ_{Т,p max}, (4)

Для максимально возможного необратимого процесса ℒ=ℒ_min=0, :

, (5)

.(6)

Соотношения (5) и (6) используются в химической термодинамике для расчета изохорного и изобарного тепловых эффектов химических реакций (ТЭХР). В этом случае работа ℒ_maxпреобразуется в тепловую энергию неупорядоченного движения частиц (в теплотуи).

В случае обратимого равновесного процесса перераспределения масс (уравнения (3) и (4)) величины и- это количества теплоты, которыми ТС обменивается с окружающей средой в процессахи.ℒ_Т,Vmaxиℒ_Т,pmax- максимальные количества работы немеханического характера, которые могут быть получены от ТС в процессахи.

В случае необратимого процесса перераспределения массы в соответствии со вторым законом термодинамики работа ℒ_maxпреобразуется в теплоту, количество которого равно изменению внутренней энергиив процессе, или изменению энтальпиив процессе, протекающем в сложных термодинамических системах.

Химические реакции, при которых теплота отводится от термодинамической системы , чтобы конечные продукты имели ту же температуру, что и начальные реагенты, называются экзотермическими химическими реакциями. Химические реакции, сопровождающиеся поглощением теплоты, приT=const, называются эндотермическими химическими реакциями.

Рассмотрим два примера: 1. разрядка химического источника электроэнергии (аккумулятор, батарея карманного фонаря) – процесс обратимый: ℒ_Т,pmax- преобразуется в электрическую энергию, а- отводится от системы. 2. Если замкнуть клеммы батареи накоротко, то получим максимально необратимый процесс:ℒ,.