1vvedenie_v_ekologicheskoe_modelirovanie

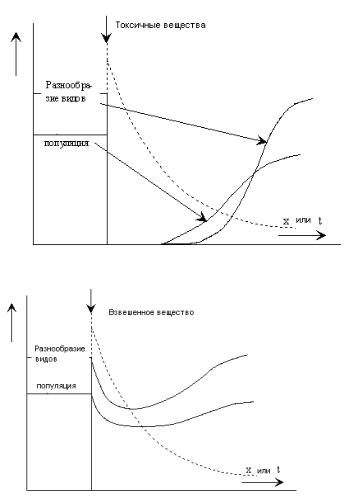
(a)

(b)

Рисунок 7.17 - Влияние а ) токсических веществ, б) взвешенных твер дых частиц на экосистему реки.

Для оценки риска загрязнения реки были разработаны различ - ные математические модели. Большинство из них показываю т отношение между органическими веществами (БПК) и растворенным ки-

189

слородом (РК). Отдельно есть модели, ко торые описывают перенос нитратов в реке. Чис ленное имитационное моделирование, ме тод Монте-Карло и метод анализа качества во ды в различные периоды времени тоже можно применить для анализа риска загрязнения. Все они кратко описываю тся в следующей главе .

Математические модели с физическим обоснованием

При описании качества воды в реке, математические модели с физическим обоснованием описывают механизмы управления движ е- нием загрязняющих веществ в одномерном пространстве. Э то

(1)адвекция со средней скоростью U;

(2)турбулентная дисперсия с коэффициентом DT;

(3)био химические взаимодейс твия.

Закон со хранения масс n количества химических веществ C i, где

i = 1, 2,..., n может быть выражено набором сдвоенных, нелинейных, частично дифференциальных уравнений в виде

ское произведение , зависящее от температуры или коэффициент истощения видов i.

Если рассматривать о дно загрязняю щее вещество, при и DT = const, уравнение (27) можно сохранить в форме уравнения одно мерной

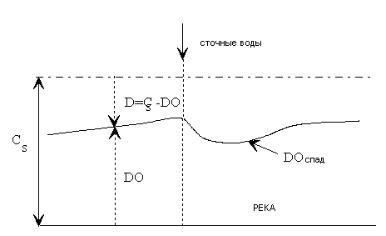
где Cs – концентрация насыщения растворенным кислородом (рисунок 7.18). Используя формулы (29) и (30), отношения между коэффициентами биологического потребления кислорода и конечной концентрации растворенного кислорода принимают форму следующих дву х дифференциальных уравнений в частных произво дных.

Рисунок 7.18 - Схематический вид кривой дефицита кислорода

K2 коэффициент реаэрации (T-1), который зависит от турбулентности по тока возле свободной повер хности во ды, скорости ве тра и т.д.

191

Эмпирические соотношения даю т:

где

U – средняя скорость (м/с), и

H – средняя глубина во ды (м)

Решение уравнений (31), (32) дает кривую дефицита кислорода (рисунок 7.18): рядом с местом сброса сточной воды БПК высокое и дефицит кислорода увеличивается вниз по течению. Затем, в связи с реаэрацией, дефицит постепенно снижается.

Более сложные модели с физическим обоснованием могут быть построены на основе уравнения (27). Например, химическую кинетику первого порядка можно использовать для представления процесса нитрификации, то есть разложения органического азо та и аммонийного азота до нитратного азота путем нитритно -азотно го преобразования

(Thomann и др., 1971)

ЛИТЕРАТУРА

Ганулис, Ж. (1994): Анализ риска загрязнения воды : вероятности и нечеткие множества, Вайнхайм, НьюЙорк, Базель, Кембридж, Токио, 306 с.

192

8 ТЕХНОЛОГИИ БЛУ ЖДАНИЯ Ч АСТИЦ ДЛЯ ОЦЕНКИ КАЧ ЕСТВА ВОДЫ

ВВЕДЕНИЕ

В этой лекции более подробно рассматриваются проблемы оценки загрязнения воды

Количественная оценка риска загрязнения в прибрежной, ре ч- ной и в зоне во доносного слоя анализируется с помощью соо тветственных численных технологий блуждания частиц, имитирующих движение, дисперсию, и физико -химические реакции.

В лекции показывается также пример использования подобных подхо дов для залива Термайкос (Греция).

1 МОДЕЛИРОВА НИЕ СЛУЧАЙНОГ О БЛУЖДА НИЯ

Рассмотрим одномерную диффузию массы M в период времени t = 0 на бесконечно малом расстоянии от x = 0 (рисунок 8.1). Математически начальное состояние будет записано следующим о бразом:

Считая, ч то масса M распространяется с помощью диффузии без переноса, концентрация C(x,t) – решение уравнения о дномерного

с нулевым средним и вариацией 2.

193

Рисунок 8.1 - Диффузия массы, введенной в момент времени t = 0 при x = 0

Предположим теперь, что частица, расположенная в точке x = 0, совершает случайные колебания между максимальными ра с- стояниями +x или -x с равной вероятностью. Для однородной функции распределения вероятностей p(x) мы получим

В соответствии с центральной предельной теоремой, после n шагов, пло тность распределения вероятностей P(x,t) – Гауссова со

средним значением

n m = 0

и отклонениями

S2 = n s2

Это означает, что

194

Сравнивая уравнения (8) и (3) или (4), мы получаем, что оба решения идентичны, если

равномерно распределена между -1 and +1, тогда уравнение (10) принимает следующую форму

x = 6 D t rnd (-1, +1) (11)

Моделирование случайного блуждания уравнения о дномерной диффузии (2), при начальных условиях (1) нужно решать в соот ветствии со следующими шагами (Ганулис ,1977):

(1)Вво дится большое количество N частиц при x = 0, t = 0;

(2)Частицы движутся с увеличением времени t. Если xn,p –

положение частицы p во время n t, тогда ее положение xn+1,p во время (n+1)t должно быть:

(3)Подсчитывается количество частиц, расположенных м ежду x

-x/ 2 и x + x/2, и делится на общее количество N частиц, таким образом можно получить численную аппроксимацию уравнения (4) или уравнения (8).

В соответствии с принципом случайного блуждания, вероятность найти частицу в заданном положении после периода времени t сооветствует распределению Гаусса со средним значением 0 и откло-

где u, v, w – компоненты скорости потоков, и x1, x2, x3 – случайные переменные, соответвтвующие нормальному распределению

со средним значением 0 и отклонением s2=2 t D.

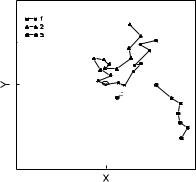
Эта процедура показана на рисунке 8.2 для трех частиц, изна - чально нахо дящихся в о дной и точке A. Каждая частица движется в соответствии с уравнениями (14) и (15). Через 10 промежутков врем е- ни частицы занимают три различных положения - A1, A2 и A3.

A2

A 1

A

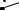
A3

Рисунок 8.2 - Случайное блуждание трех частиц после 10 пр о- межутков времени

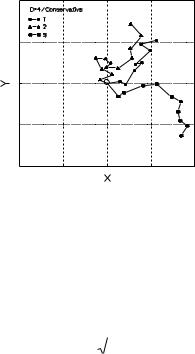
Чтобы оценить вероятность и концентрацию частиц, площадь покрыта решеткой (рисунок 8.3). Зная компоненты скорости u, v в точках решетки, можно подсчитать скорость движения частиц с помощью линейной интерполяции. Вероятность о казаться в данной ячейке р е- шетки, и, соответственно, концентрация частиц оценивается при по д- счете количества частиц, ко торое оказалось в ячейке реше тки.

196

Рисунок 8.3 - Решетка, наложенная на рисунок случайного б луждания трех частиц

Если вместо начальных условий (1) мы введем непрерывную

тогда аналитическое решение уравнения диффузии (2) со скоростью адвекции U будет следующим

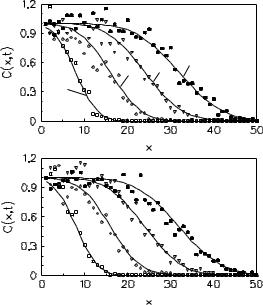
Проверка достоверности модели случайного блуждания о тображена на рисунках 8.4 и 8.5 в предыдущей главе для D=1 и D=0.01 м2/с, соответственно. Во всех случаях мы имеем U=1 м/с и x =1 м; это означает, числа Пекле , основанные на x принимают значения 1

и 100.

При введении в 10 раз большего ко личества частиц (рисунок 8.4), колебания случайного блуждания про должаю тся, хотя первая волна хорошо показана на рисунке 8.5 для высоких чисел Пекле

(Ganoulis, 1977).

197

(a)

(b)

Рисунок 8.4- Сравнение между аналитическим решением и моделью случайного блуждания для (a) N=1,000 и (b) N=10,000 (малые числа Пекле )

198