Завдання 7.

(Виробнича функція)

Припустимо що виробнича регресія (Кобба-Дугласа) має вигляд:

(1)

е Y-обсяг випущеної продукції;

X₁- основні засоби розглянутої галузі;

X₂- працезатрати.

На основі статистичних даних, використовуючи МНК, знайти:

- оцінки параметрів виробничої регресії.;

- надійністю p=0,95 встановити адекватність прийнятої математичної моделі статистичним даним;

- провести дисперсійний та кореляційний аналіз регресії;

- перевірити залишки моделі на наявність автокореляції залишків;

- знайти частині та сумарний коефіцієнти еластичності та зробити їх економічний аналіз;

- записати вирази для граничної продуктивність і граничного продукту даної регресії;

- обчислити значення прогнозу і його надійний інтервал.

- побудувати ізокванти для Y=172.

Рішення

1. Для оцінки параметрів виробничої регресії приводимо її до лінійної форми. Після логарифмування і заміни величин Y₁=ln(Y),Z₁=ln(x1),Z₂=ln(x2) отримаємо приведену лінійну регресію:

Y1=a₀₁+a₁z+a₂x2, де a₀₁=lna₀ (2.)

Знаходимо оцінки параметрів моделі методом 1МНК за даними таблиці 11

Таблиця 11

Додаткові розрахунки для знаходження оцінок параметрів моделі

	X1	X2	Y	Z1	Z2	Y1
1	50	90	152	3,912	4,500	5,024
2	60	100	172	4,094	4,605	5,147
3	70	110	192	4,248	4,700	5,257
4	80	120	213	4,382	4,787	5,361
5	90	130	232	4,500	4,868	5,447
6	100	140	253	4,605	4,942	5,533
7	110	150	275	4,700	5,011	5,617
8	120	160	293	4,787	5,075	5,680
9	130	170	314	4,868	5,136	5,749
10	140	180	334	4,942	5,193	5,811
11	150	190	354	5,011	5,247	5,869
прогноз	160	200	1	5,075	5,298

Застосовуючи пакет аналіз «Регресія» табличного процесору Excel отримали наступні дані (Таблиця 12.2)

Таблиця 12.2

Результати регресійного аналізу виробничої функції

Регресійна статистика
Множинний R	0,99
R-квадрат	0,99
Нормований R-квадрат	0,99
Стандартна помилка	0,0022
Спостереження	11,00
Дисперсійний аналіз
	df	SS	MS	F	Значущість F
Регресія	2,00	0,77	0,39	46610,73	5,4Е-17
Остаток	8,00	0,00	0,00
Усього	10,00	0,77
Коефіцієнти		Стандартна помилка	t-статистика	P-Значення	Нижня межа 95%	Верхня межа 95%
Y-пересечение	0,51	0,14	3,70	0,01	0,19	0,51
Переменная X 1	0,22	0,05	4,19	0,00	0,10	0,22
Переменная X 2	0,81	0,08	10,68	0,00	0,64	0,81

Маємо a₀₁=0,51 A₁=0,22 A₂=0,81

Для визначення коефіцієнту а₀ знайдемо використаємо обернену функцію до натурального логарифму – експотенційну. Отже а₀ = =1,66. Таким чином наша регресія має вигляд:

(3)

Для визначення адекватності вибраної математичної моделі скористуємося обрахованими значеннями таблиці 11.3, стовпця (Значущість F), що дорівнює . Отже, для заданого рівня довіри 0,95% ,так як , приймається гіпотеза про адекватність моделі статистичним даним.

2. Для обчислення помилки регресії підставимо вхідні значення х1, а х2 у рівняння (11.8) і обчислимо її за формулою :

, (4)

де - кількість спостережень (11/8), а - кількість факторних змінних (2). Маємо:.

Обчислена помилка незначна. Для рівняння регресії коефіцієнт детермінації теж розраховується автоматично в процесі знаходження коефіцієнтів регресії ( =0,99 — табл.11, рядок «R-квадрат». Він показує, що 99,9% варіації змінної у пояснюється зміною . На долю чинників, які не увійшли до рівняння (12.3), приходиться 0,01% варіації результативної ознаки (у).

Про якість кореляційного зв’язку свідчать і нормований та звичайний коефіцієнт кореляції.

Надійність побудованої моделі визначається надійністю множинних кореляційних зв’язків та надійністю окремих коефіцієнтів регресії.

Перевірка надійності окремих коефіцієнтів регресії по t-критерію Стьюдента в стовпці t – Статистика показують що всі фактичні значення t менше теоретичного 2,04. Тому всі змінні, що увійшли до рівняння, є надійними, суттєво відмінними від нуля.

%-ві нижні та верхні довірчі інтервали коефіцієнтів регресії наводяться у стовпчиках «Нижні 95%» і «Верхні 95%» (табл.11).

4. Для перевірки на наявність автокореляції залишків застосовуємо Критерий Дарбина-Уотсона (Дані представлені у таблиці 12.3)

Знайдемо оцінку критерію Дарбіна-Уотсона

DW=16,29. Порівнюємо значення DW з табличним для рівня P=0,05 n=12 .DW1 табл=0,9 DW2 табл=1,35

Висновок залишки не мають автокореляцію.

Таблиця 12

Таблиця додаткових даних для обчислення автокореляції

№	U2	Ut-U(t-1)	(Ut-U(t-1))2	Ut*U(t-1)
1	0,03
2	0,02	-0,02	0,00	0,00
3	0,14	0,13	0,02	0,00
4	0,16	0,02	0,00	0,02
5	0,67	0,51	0,26	0,11
6	0,00	-0,67	0,45	0,00
7	2,95	2,94	8,67	0,01
8	0,29	-2,65	7,04	0,86
9	0,03	-0,26	0,07	0,01
10	0,01	-0,02	0,00	0,00
11	0,20	0,18	0,03	0,00
сума	4,51	0,17	16,54	1,02

Згідно теорії, частинні коефіцієнти еластичності функції Кобба-Дугласа дорівнюють оцінкам параметрів моделі

Сумарний коефіцієнт еластичності дорівнює сумі частинних:

Так як значення загального коефіцієнта еластичності більше одиниці, то збільшення факторів виробництва в (стале число більше одиниці) разів викличе збільшення обсягу виробництва в число разів більше за , тобто в . В даному випадку маємо економію ресурсів на масштабах виробництва.

6. Граничною продуктивністю праці (ГПП) називається зміна обсягу виробництва продукції за рахунок зміни працезатрат на одиницю при незмінних інших факторах, що впливають на обсяг виробництва продукції. Для нашого випадку вона дорівнюватиме:

(5)

Граничним продуктом праці називається додатковий продукт , отриманий у результаті додаткових затрат праці при незмінних затратах решти факторів виробництва.

7.Для обчислення довірчого інтервалу оцінки прогнозного значення обчислюємо точковий прогноз для , .

Підставляємо ці значення в формулу (12.3) маємо:

Побудуємо довірчий інтервал для прогнозного значення за формулою:

(5)

де - табличне значення критерію Ст’юдента, - середнє квадратичне відхилення дисперсії залишків.

- вектор прогнозованих даних, - - матриця коваріацій.

Для наочного уявлення взаємо змінюваності факторів побудуємо ізокванти для Y=172. Ізокванта залежності Х₁ від Х₂ має вигляд:

(6)

Якщо сталу:

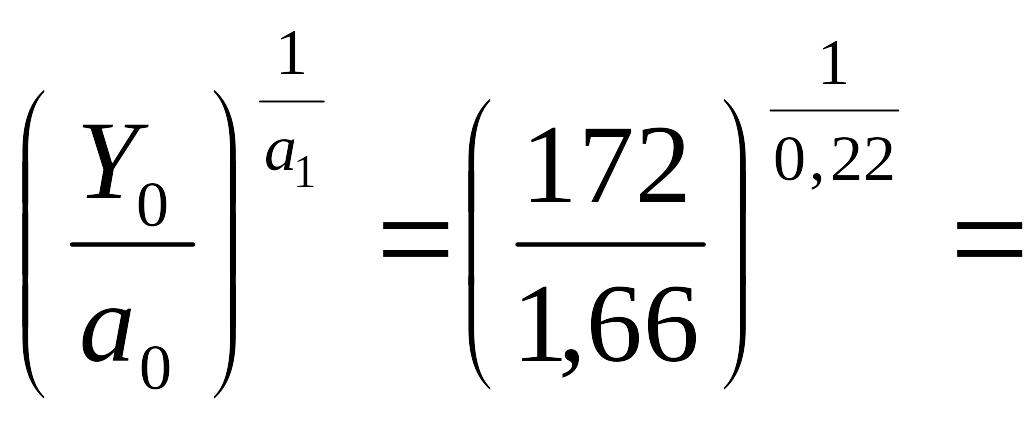
позначити через b, то отримаємо таку залежність:

Графік ізокванти має вигляд:

Рис. 1 Графік ізокванти для сталого значення У.