3. Понятие вариации.
Различия индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака.
Это изменение возникает в результате того, что индивидуальные значения складываются по совокупным факторам, которые по-разному действуют на совокупность целого.
Средняя величина– это абстрактная обобщающая характеристика признака изучаемой совокупности.
Она не дает данные о том, как отдельные значения изучаемой совокупности группируются вокруг средней.
Колеблимость отдельных значений характеризуют показатели вариации. Термин «вариация» происходит от латинского и обозначает – изменения, колеблимость.
Под вариацией в статистике понимают такие количественные изменения в пределах одного признака в однородной совокупности, которые обусловлены и зависят от влияния различных факторов.
Анализ статистической совокупности позволяет оценить степень зависимости изучаемой совокупности и ее признаков от ее факторов.
Пример.
Изучая вариацию можно определить однородность совокупности. Степень близости данных отдельных единиц xк средней измеряются рядом абсолютных, относительных и средних показателей вариации.
4. Показатели вариации.
Несгрупированый ряд Сгруппированный ряд
|
1-й показатель-размах вариации отклонение максимального признака от минимального | |
|
| |
|
|
|
|
2-й показатель – среднее линейное отклонение – представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их среднего значения. | |
|
|
|
|
| |
|
|
|
|
3-ий показатель – дисперсия– представляет собой средний квадрат отклонений вариант от их среднего значения. | |
|
|
|
|
4-ый показатель – седнее квадратическое отклонение– представляет собой корень из дисперсии. | |
|
|
|
|
|
|
- это абсолютное
значение (модель) отклонения значения
варианты от ее ср. величины. 
5-ый показатель. Коэффициент вариации – это отношение седнего квадратического отклонения к среднему значению.
Коэффициент вариации применяется в следующих случаях:
когда необходимо определить и сравнить степени рассеивания 2-х или нескольких признаков, выраженных в различных единицах измерения для характеристики одной и той же совокупности;
когда необходимо определить рассеивание одного и того же признака в разных единицах совокупности, имеющих разные единицы измерений и разные ср. величины.
Если коэффициент вариации составляет более 0,40 то такая совокупность считается неоднородной.
Пример.
Имеются данные о стаже работы рабочих 3-х бригад:
Iбригада – 15, 18, 20, 22, 25 лет;
IIбригада – 10, 15, 20, 25, 30 лет;
IIIбригада – 8, 12, 17, 25, 38 лет.
Определить показатель вариации.
1. Размах вариации.
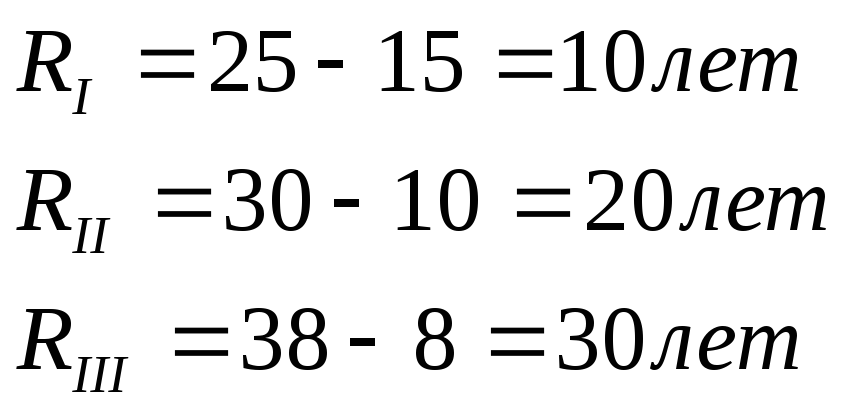
2. Среднее линейное отклонение.
I.
II.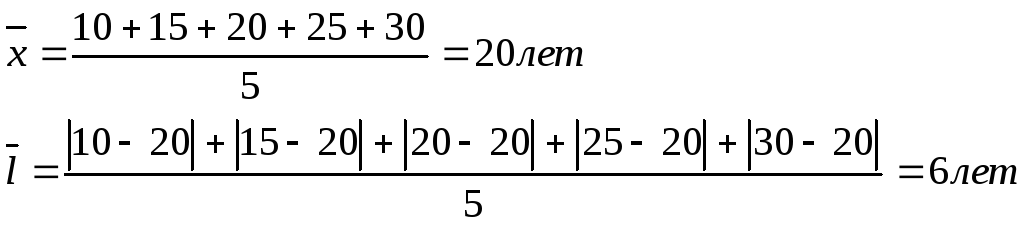
III.
В Iбригаде абсолютное отклонение каждого значения от средней величины 2,8 лет, воIIбригаде – 6 лет, вIIIбригаде – 9,2 лет.
3. Дисперсия, средний квадрат отклонения.
I.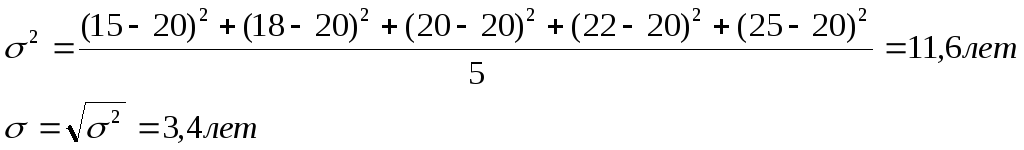
II.
III.
Чем больше ср. квадратическое отклонение, тем более высока вариация, т.е. более неточным будет среднее значение.
4. Коэффициент вариации.
I.
II.
III.
IIIбригада является неоднородной совокупностью, т.к. коэффициент вариации составляет более 0,40.