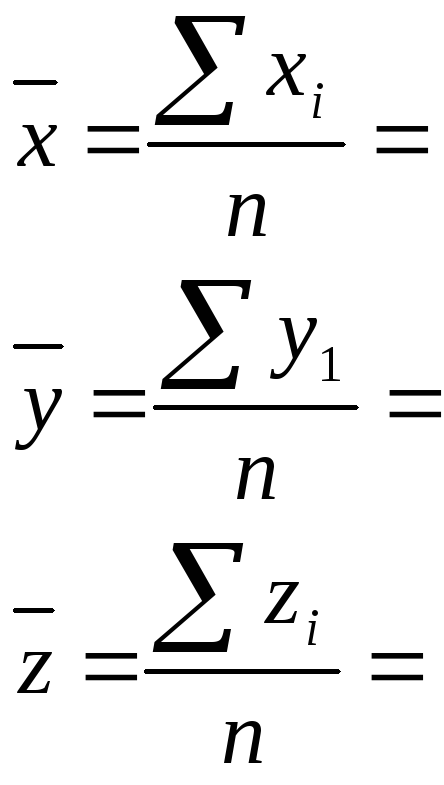Федеральное агентство по образованию
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра АСУ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
по дисциплине «Статистика»
Вариант 907578
Выполнил:
студ. гр. ПИЭ-208в
Вершинина К.И.
Проверил:
проф. Арьков В.Ю.
Уфа 2008
Упорядоченные данные
-
N
X
Y
Z
G
1
0
-463
-162
45
2
0
-411
-109
32
3
1
-411
-108
36
4
3
-411
-73
43
5
3
-397
-71
39
6
5
-326
-71
52
7
8
-322
-68
57
8
9
-305
-67
54
9
11
-305
-59
61
10
12
-289
-52
64
11
14
-283
-50
67
12
15
-281
-42
61
13
15
-281
-41
52
14
16
-265
-41
59
15
18
-248
-39
50
16
18
-219
-39
50
17
21
-194
-34
57
18
22
-180
-19
57
19
22
-179
-18
62
20
26
-177
-10
70
21
29
-168
-3
74
22
29
-166
-2
76
23
29
-142
-1
74
24
30
-133
4
69
25
31
-126
4
66
26
31
-99
7
63
27
33
-98
11
68
28
33
-65
16
62
29
35
-41
30
65
30
39
-30
33
69
31
40
-22
33
79
32
41
-19
43
88
33
42
0
49
87
34
44
12
70
91
Задача 1.
Вычислите показатели вариации по выборкам X, Y, Z:
- среднее арифметическое;
- моду;
-медиану; -размах вариации;
-дисперсию;
- стандартное отклонение;
- среднее линейное отклонение;
- коэффициенты осцилляции и вариации.
Решение.
1.1Среднее арифметическое
|
|
| |
|
725/34 = 21,3235 | ||
|
| ||
|
| ||
|
-7044/34 = -207,1765 | ||
|
| ||
|
| ||
|
-879/34 = -25,8529 | ||
|
|
1.2 Мода
|
Mox= |
29 |
|
Moy= |
-411 |
|
Moz= |
-71 |
|
Moz= |
-41 |
|
Moz= |
-39 |
|
Moz= |
4 |
|
Moz= |
33 |
1.3 Медиана
Т.к. объем выборки четный, то значение медианы находиться как среднее между центральными значениями выборки:
|
Mex= |
21,5 |
|
Mey= |
-187 |
|
Mez= |
-26,5 |
1.4 Размах вариации
|
Rx = |
maxx-minx |
44 |
|
Ry = |
maxy-miny |
475 |
|
Rz = |
maxz-minz |
232 |
1.5 Дисперсия
|
|
|
|
|
|
|
|
21,3235 |
255,8235 |
136,1471 |
454,6917 |
65445,6632 |
18536,0328 |
|
21,3235 |
203,8235 |
83,1471 |
454,6917 |
41544,0192 |
6913,4402 |
|
20,3235 |
203,8235 |
82,1471 |
413,0447 |
41544,0192 |
6748,146 |
|
18,3235 |
203,8235 |
47,1471 |
335,7507 |
41544,0192 |
2222,849 |
|
18,3235 |
189,8235 |
45,1471 |
335,7507 |
36032,9612 |
2038,2606 |
|
16,3235 |
118,8235 |
45,1471 |
266,4567 |
14119,0242 |
2038,2606 |
|
13,3235 |
114,8235 |
42,1471 |
177,5157 |
13184,4362 |
1776,378 |
|
12,3235 |
97,8235 |
41,1471 |
151,8687 |
9569,4372 |
1693,0838 |
|
10,3235 |
97,8235 |
33,1471 |
106,5747 |
9569,4372 |
1098,7302 |
|
9,3235 |
81,8235 |
26,1471 |
86,9277 |
6695,0852 |
683,6708 |
|
7,3235 |
75,8235 |
24,1471 |
53,6337 |
5749,2032 |
583,0824 |
|
6,3235 |
73,8235 |
16,1471 |
39,9867 |
5449,9092 |
260,7288 |
|
6,3235 |
73,8235 |
15,1471 |
39,9867 |
5449,9092 |
229,4346 |
|
5,3235 |
57,8235 |
15,1471 |
28,3397 |
3343,5572 |
229,4346 |
|
3,3235 |
40,8235 |
13,1471 |
11,0457 |
1666,5582 |
172,8462 |
|
3,3235 |
11,8235 |
13,1471 |
11,0457 |
139,7952 |
172,8462 |
|
0,3235 |
13,1765 |
8,1471 |
0,1047 |
173,6202 |
66,3752 |
|
0,6765 |
27,1765 |
6,8529 |
0,4577 |
738,5622 |
46,9622 |
|
0,6765 |
28,1765 |
7,8529 |
0,4577 |
793,9152 |
61,668 |
|
4,6765 |
30,1765 |
15,8529 |
21,8697 |
910,6212 |
251,3144 |
|
7,6765 |
39,1765 |
22,8529 |
58,9287 |
1534,7982 |
522,255 |
|
7,6765 |
41,1765 |
23,8529 |
58,9287 |
1695,5042 |
568,9608 |
|
7,6765 |
65,1765 |
24,8529 |
58,9287 |
4247,9762 |
617,6666 |
|
8,6765 |
74,1765 |
29,8529 |
75,2817 |
5502,1532 |
891,1956 |
|
9,6765 |
81,1765 |
29,8529 |
93,6347 |
6589,6242 |
891,1956 |
|
9,6765 |
108,1765 |
32,8529 |
93,6347 |
11702,1552 |
1079,313 |
|
11,6765 |
109,1765 |
36,8529 |
136,3407 |
11919,5082 |
1358,1362 |
|
11,6765 |
142,1765 |
41,8529 |
136,3407 |
20214,1572 |
1751,6652 |
|
13,6765 |
166,1765 |
55,8529 |
187,0467 |
27614,6292 |
3119,5464 |
|
17,6765 |
177,1765 |
58,8529 |
312,4587 |
31391,5122 |
3463,6638 |
|
18,6765 |
185,1765 |
58,8529 |
348,8117 |
34290,3362 |
3463,6638 |
|
19,6765 |
188,1765 |
68,8529 |
387,1647 |
35410,3952 |
4740,7218 |
|
20,6765 |
207,1765 |
74,8529 |
427,5177 |
42922,1022 |
5602,9566 |
|
22,6765 |
219,1765 |
95,8529 |
514,2237 |
48038,3382 |
9187,7784 |
|
387 |
3804,353 |
1373 |
5879,4428 |
586736,9428 |
83082,2634 |
|
|
| |
|
5879,4428/34 = 178,1649 | ||
|
| ||
|
| ||
|
586736,9428/34 = 17779,9074 | ||
|
| ||
|
| ||
|
83082,2634/34 = 2517,6443 | ||
|
|
