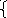7.1 Сравнение дисперсий.

При заданном уровне значимости должно выполняться следующее неравенство:

Рассчитаем распределение Фишера для уровней значимости α=32%; 5%; 0,3%:

Рассчитаем распределение Фишера для уровней значимости α=32%; 5%; 0,3%:

Уровни значимости α
32%	0,7049	1,4187	0,01
5%	0,4994	2,0023	0,01
0,30%	0,3449	2,8996	0,01

При всех уровнях значимости α=32%; 5%; 0,3% неравенство не выполняется, следовательно гипотезу отвергаем.

7.2 Проверка гипотезы о среднем значении.

Рассмотри случайную величину .

Для проверки вычислим фактическую t – статистику:

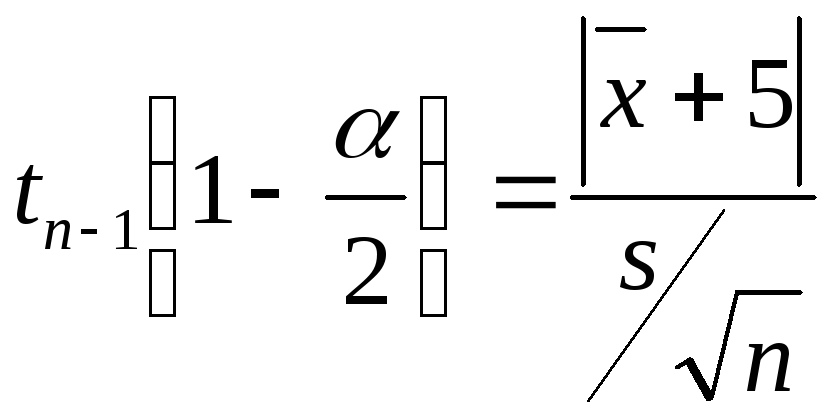
t_факт.=

t_кр=;

Проверка гипотезы о среднем значении

α	tкр.	Сравнение	tфакт.
0,32	1,0355	<	11,4994
0,05	2,167	<	11,4994
0,003	3,3185	<	11,4994

Из расчетов видно, что для всех уровней значимости α=32%; 5%; 0,3% t_факт> t_кр , следовательно гипотезу отвергаем.

7.3 Сравнение средних.

При изучении выборочных оценок используется распределение Стьюдента с числом степеней свободы df=n₁+n₂-2:

t_факт.=

t_кр.=;

Сравнение средних

α	tкр.	Сравнение	tфакт.
0,32	1,0272	<	9,9425
0,05	2,122	<	9,9425
0,003	3,1899	<	9,9425

Из расчетов видно, что для всех уровней значимости α=32%; 5%; 0.3% t_факт> t_кр , следовательно гипотезу отвергаем.

Задача 8.

Вычислите линейный коэффициент корреляции r_yx и r_zx. Сделайте вывод о тесноте линейной связи между признаками.

Решение.

Линейный коэффициент корреляции вычисляется по формуле:

Расчет показателей

Xi	Yi	X2	XY	Y2
0	-41	0	0	1681
40	-397	1600	-15880	157609
42	-411	1764	-17262	168921
21	-180	441	-3780	32400
35	-281	1225	-9835	78961
31	-322	961	-9982	103684
22	-219	484	-4818	47961
15	-166	225	-2490	27556
29	-281	841	-8149	78961
33	-289	1089	-9537	83521
30	-283	900	-8490	80089
1	-22	1	-22	484
9	-19	81	-171	361
3	12	9	36	144
15	-126	225	-1890	15876
18	-168	324	-3024	28224
3	0	9	0	0
26	-248	676	-6448	61504
0	-65	0	0	4225
31	-305	961	-9455	93025
14	-142	196	-1988	20164
29	-265	841	-7685	70225
8	-99	64	-792	9801
41	-411	1681	-16851	168921
33	-326	1089	-10758	106276
44	-463	1936	-20372	214369
11	-133	121	-1463	17689
18	-179	324	-3222	32041
16	-194	256	-3104	37636
22	-177	484	-3894	31329
39	-411	1521	-16029	168921
5	-30	25	-150	900
29	-305	841	-8845	93025
12	-98	144	-1176	9604
725	-7044	21339	-207526	2046088

-0,9473

|r_xy|>0,7 – существенная линейная зависимость

Расчет показателей

Xi	Z	X2	XZ	Z2
0	-19	0	0	361
40	-67	1600	-2680	4489
42	16	1764	672	256
21	-1	441	-21	1
35	-52	1225	-1820	2704
31	-41	961	-1271	1681
22	43	484	946	1849
15	7	225	105	49
29	-41	841	-1189	1681
33	-39	1089	-1287	1521
30	-68	900	-2040	4624
1	-3	1	-3	9
9	11	81	99	121
3	-2	9	-6	4
15	33	225	495	1089
18	-50	324	-900	2500
3	49	9	147	2401
26	33	676	858	1089
0	-42	0	0	1764
31	-39	961	-1209	1521
14	4	196	56	16
29	-108	841	-3132	11664
8	70	64	560	4900
41	-109	1681	-4469	11881
33	-162	1089	-5346	26244
44	-71	1936	-3124	5041
11	-18	121	-198	324
18	-34	324	-612	1156
16	4	256	64	16
22	-10	484	-220	100
39	-59	1521	-2301	3481
5	30	25	150	900
29	-73	841	-2117	5329
12	-71	144	-852	5041
725	-879	21339	-30645	105807

-0,5227

0<|r_yx|<1 – линейная зависимость на фоне случайных отклонений.

Задача 9.

Вычислите коэффициенты корреляции рангов Спирмена и Кендалла Y(X) Z(X). Сделайте вывод о тесноте связи.

Решение.

Для вычисления коэффициентов корреляции рангов Спирмена исходные данные ранжируют, т.е. расставляют по порядку возрастания/убывания. Рангом является порядковый номер.

9.1 Коэффициент корреляции рангов Спирмена.

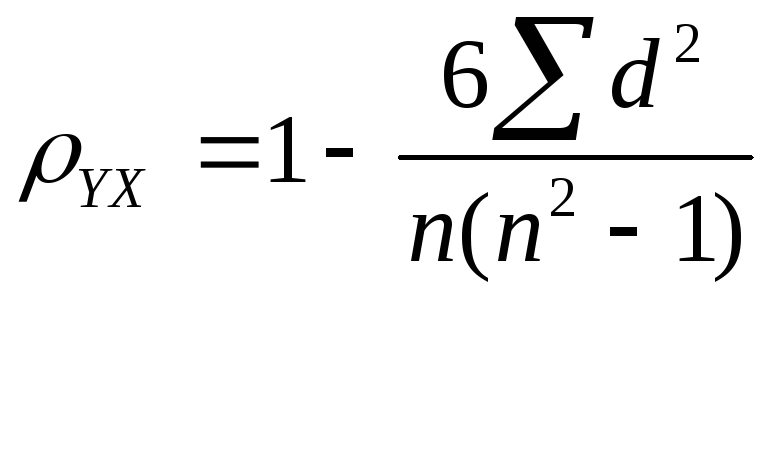d – разность рангов x и y: d_i=R(x_i)-R(y_i);

n – число наблюдений, число пар, число разностей рангов.

Коэффициент корреляции рангов Спирмена

Rx	Ry	d	d2
1,5	29	-27,5	756,25
31	5	26	676
33	3	30	900
17	18	-1	1
29	12,5	16,5	272,25
25,5	7	18,5	342,25
18,5	17	1,5	2,25
12,5	22	-9,5	90,25
22	12,5	9,5	90,25
27,5	10	17,5	306,25
24	11	13	169
3	31	-28	784
8	32	-24	576
4,5	34	-29,5	870,25
12,5	25	-12,5	156,25
16	21	-5	25
4,5	33	-28,5	812,25
20	15	5	25
1,5	28	-26,5	702,25
25,5	8,5	17	289
11	23	-12	144
22	14	8	64
7	26	-19	361
32	3	29	841
27,5	6	21,5	462,25
34	1	33	1089
9	24	-15	225
16	19	-3	9
14	17	-3	9
18,5	20	-1,5	2,25
30	3	27	729
6	30	-24	576
22	8,5	13,5	182,25
10	27	-17	289
			12828,5

-0,96 – связь статистически значима.

Коэффициент корреляции рангов Спирмена

Rx	Rz	D	d2
1,5	18	-16,5	272,25
31	8	23	529
33	28	5	25
17	23	-6	36
29	10	19	361
25,5	13,5	12	144
18,5	32	-13,5	182,25
12,5	26	-13,5	182,25
22	13,5	8,5	72,25
27,5	16	11,5	132,25
24	7	17	289
3	21	-18	324
8	27	-19	361
4,5	22	-17,5	306,25
12,5	30,5	-18	324
16	11	5	25
4,5	33	-28,5	812,25
20	30,5	-10,5	110,25
1,5	12	-10,5	110,25
25,5	16	9,5	90,25
11	24,5	-13,5	182,25
22	3	19	361
7	34	-27	729
32	2	30	900
27,5	1	26,5	702,25
34	5,5	28,5	812,25
9	19	-10	100
16	17	-1	1
14	24,5	-10,5	110,25
18,5	20	-1,5	2,25
30	9	21	441
6	29	-23	529
22	4	18	324
10	5,5	4,5	20,25
			9903

-0,5131 – связь статистически незначима.

9.2 Коэффициент корреляции рангов Кендалла.

, S=P-Q

Коэффициент корреляции рангов Кендалла

X	RX	Y	Z	Y соот. зн Х	Ранги Y	Z соот. Зню Х	Ранги Z
0	1	-463	-162	-41	29	-19	18
0	2	-411	-109	-65	28	-42	12
1	3	-411	-108	-22	31	-3	21
3	4	-411	-73	12	34	-2	22
3	5	-397	-71	0	33	49	33
5	6	-326	-71	-30	30	30	29
8	7	-322	-68	-99	26	70	34
9	8	-305	-67	-19	32	11	27
11	9	-305	-59	-133	24	-18	19
12	10	-289	-52	-98	27	-71	5,5
14	11	-283	-50	-142	23	4	24,5
15	12	-281	-42	-166	22	7	26
15	13	-281	-41	-126	25	33	30,5
16	14	-265	-41	-194	17	4	24,5
18	15	-248	-39	-168	21	-50	11
18	17	-219	-39	-179	19	-34	17
21	17	-194	-34	-180	18	-1	23
22	18	-180	-19	-219	17	43	32
22	19	-179	-18	-177	20	-10	20
26	20	-177	-10	-248	15	33	30,5
29	21	-168	-3	-281	12,5	-41	13,5
29	22	-166	-2	-265	14	-108	3
29	23	-142	-1	-305	8,5	-73	4
30	24	-133	4	-283	11	-68	7
31	25	-126	4	-322	7	-41	13,5
31	26	-99	7	-305	8,5	-39	16
33	27	-98	11	-289	10	-39	16
33	28	-65	16	-326	6	-162	1
35	29	-41	30	-281	12,5	-52	10
39	30	-30	33	-411	3	-59	9
40	31	-22	33	-397	5	-67	8
41	32	-19	43	-411	3	-109	2
42	33	0	49	-411	3	16	28
44	34	12	70	-463	1	-71	5,5

-0,8467

-0,3601

Задача 10.

Постройте уравнения регрессии графическим способом. Нанесите линии регрессии на корреляционное поле.

Решение.

Проведем линии регрессии «на глаз» - по местам «сгущения» точек. На линиях регрессии и выберем по две точки , ближе к краям диапазона значений. Составим систему уравнений - два уравнения с двумя неизвестными:

Подставим в систему значения y₁, y₂, z₁, z₂, x₁, x₂:

Получаем уравнения линии регрессии:

=-5-10х;

=63,5-3,8х.

Задача 11.

С помощью МНК постройте уравнения регрессии и . Нанесите линии регрессии на корреляционное поле.

=а+bx

n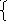a+bΣx=Σy

aΣx+bΣx²=Σxy

	34a + b725 = -7044
	725a + b21339 = -207526
	a = 0,7225
	b = -9,7497
	= 0,7225 + -9,7497x

=c+dy

nc+dΣy=Σx

cΣy+dΣy²=Σxy

	34c + d-7044 = 725
	-7044c + d2046088 = -207526
	c = 1,0828
	d = -9,77
	= 1,0828 + -9,77y

=а+bx

na+bΣx=Σz

aΣx+bΣx²=Σxz

	34a + b725 = -879
	725a + b21339 = -30645
	a = 17,3118
	b = -2,0243
	= 17,3118 + -2,0243x

=c+dy

n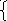c+dΣy=Σx

cΣy+dΣy²=Σxy

	34c + d-879 = 725
	-879c + d105807 = -30645
	c = 17,6201
	d = -0,1433
	= 17,6201 + -0,1433z

Задача 12.

После определения коэффициентов уравнения регрессии разными способами провести сравнение полученных оценок и построенных графиков.

Решение.

Сравним построенные уравнения регрессии

Y(X)

Графическим способом: =-5-10х;

С помощью МНК: =0,7225 + (-9,7497x)

Z(X)

Графическим способом: =63,5-3,8х.

С помощью МНК: =1,0828 + (-9,77y)

Построенные графики совпадают, с небольшими различиями, связанными с погрешностями построения линий «на глаз».Погрешность вполне допустимая.

Задача 13.

Проведите сглаживание ряда динамики G_t с помощью простой и взвешенной скользящей средней, а так же скользящей медианы по трем, пяти и двенадцати точкам. В качестве номера месяца t используется столбец N. Постройте графики исходного ряда динамики (ИРД) и сглаженных рядов.

Решение.

Для вычисления значений таблицы используем формулу для расчета простой скользящей средней:

И формулу для расчета скользящей средней взвешенной:

В качестве весов w_k используем биноминальные коэффициенты.