Агрегатные индексы

В международной статистике для построения агрегатных индексов применяются следующие обозначения:

q– физический объем произведенной продукции (количество);

p– цена;

z– себестоимость;

d– структура (удельный вес);

1 – отчетный период;

0 – базисный период.

Пример.

Вид продукции	Ед. измерения, тыс.	Июль		Август		Индивидуальные индексы
		Кол-во	Цена, руб.	Кол-во	Цена, руб.	Физического объема	Цены
Молоко	Л	5000	300	6000	276	1,2	0,92
Мясо	Ц	25000	200	32000	190	1,28	0,95
Картофель	Т	10000	120	11000	102	1,1	0,85

Индивидуальный индекс физического объема проданной продукции определяется путем деления конкретного элемента совокупности в отчетном периоде на базисный период:

Общий индекс физического объемаопределяется по формуле:

где - размер товарооборота в отчетном периоде при ценах базисного периода;

- размер товарооборота в базисном периоде.

Индекс физического объема показывает, что за счет изменения количества реализованной продукции изменяется размер товарооборота в отчетном периоде по сравнению с базисным. Товарооборот возрос на 24%. Для того, чтобы определить изменение товарооборота в натуральном выражении , необходимо из числителя общего индекса физического объема вычесть знаменатель:

=9520000-7700000=1820000рублей

Индекс цены

Общий индекс цены показывает на сколько % изменился размер товарооборота в отчетном периоде по сравнению с базисным за счет изменения индивидуальных цен. Для того, чтобы рассчитать на сколько рублей изменился товарооборот за счет изменения цен нужно применить формулу:

Вывод: общий индекс цены показывает, что на 6,96 % уменьшился размер товарооборота за счет изменения цен.

Общий индекс товарооборота

Общий индекс товарооборота показывает на сколько % изменяется товарооборот в отчетном периоде по сравнению с базисным при влиянии двух факторов и цены и физического объема. Для того, чтобы узнать на сколько рублей изменился товарооборот в отчетном по сравнению с базисным периоде, необходимо из числителя вычесть знаменатель:

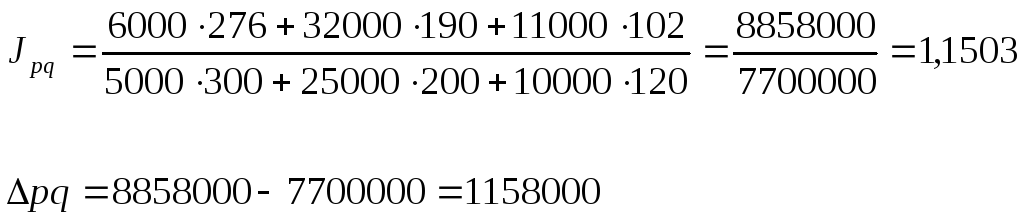
Вывод: товарооборот в августе увеличился по сравнению с июлем на 15 %.

Между индексом цены, индексом физического объема и индексом товарооборота существует взаимосвязь:

Индексы постоянного, переменного состава и индексы структурных сдвигов

Индекс постоянного составапоказывает изменение общей средней цены за счет изменения индивидуальных цен в отчетном периоде по сравнению с базисным.

Индекс структурных сдвиговпоказывает изменение средней цены в отчетном периоде за счет изменения физического объема.

Индекс переменного состава– это индекс средней цены, который показывает на сколько % средняя цена изменяется в отчетном периоде по сравнению с базисным.

Индекс переменного состава равен произведению индекса постоянного состава на индекс структурных сдвигов:

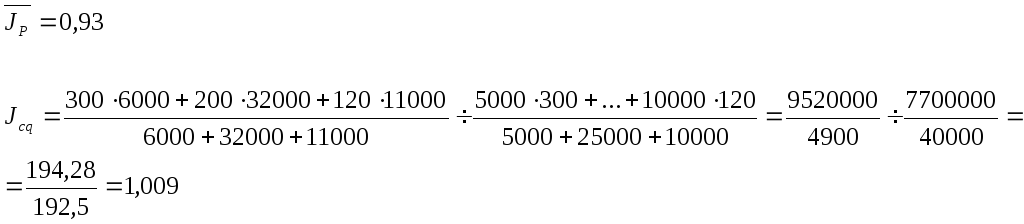
Средние индексы

Для характеристики обобщающих показателей, характеризующих изменение количественной характеристики явления, используются средние индексы.

На основе агрегатных индексов могут быть рассчитаны:

• средний арифметический индекс;

• средний гармонический индекс.

Средний арифметический индексвычисляется при исчислении индивидуального индекса физического объема. Он используется, если неизвестны данные о физическом объеме в отчетном периоде, в таком случае физический объем отчетного периода рассчитывают исходя из индивидуального индекса физического объема:

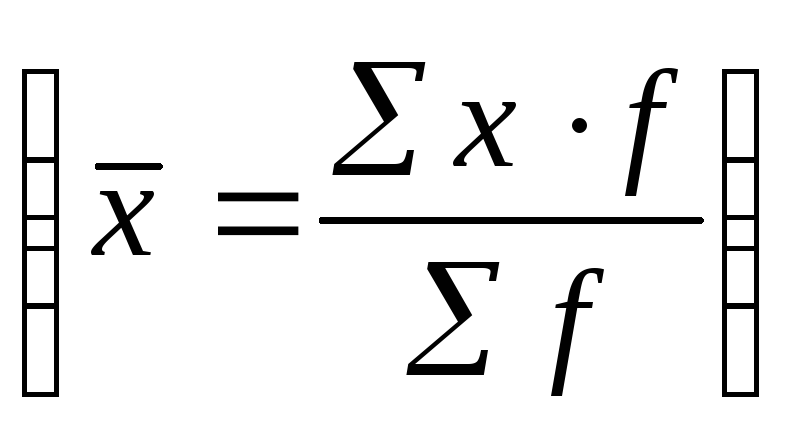
Индекс средний арифметический вычисляется:

Средний гармонический индексопределяется исходя из преобразований агрегатного индекса цены, для этого, исходя из расчета индивидуального индекса цены, определяется цена базисного периода.

Средний гармонический индекс цены вычисляется:

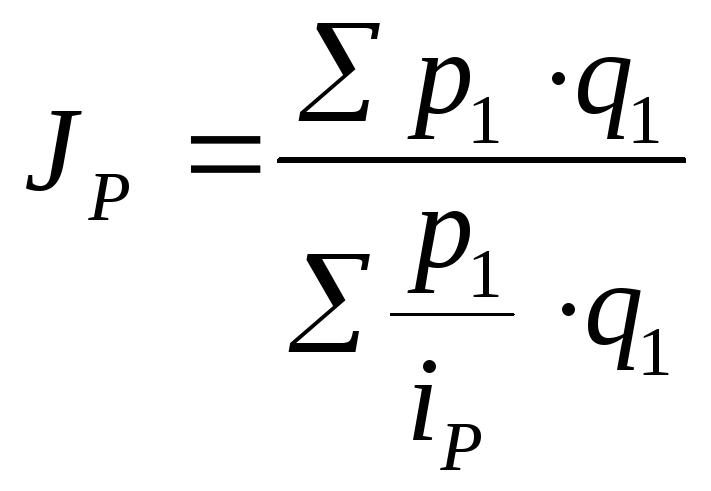
Пример.

Используя следующие данные о производстве продукции на хлебозаводе, определить общий рост физического объема в отчетном периоде по сравнению с базисным, используя взаимосвязь индексов, определить на сколько % изменились цены, если известно, что стоимость хлеба в фактических ценах выросла на 2 %.

Вид продукции	Производство продукции в базисном периоде, тыс. руб.	Изменение количества продукции в отчетном периоде по сравнению с базисным	Индивидуальные индексы
Клей IC	233	+ 5	1,05
Клей IIС	312	Без изменения	1
Клей обойный	170	- 3	0,97