Точки пересечения графика с осями координат.
График
пересекает ось
в точках с абсциссами, определяемыми
уравнением
,
т.е.
,
график пересекает ось
в точке с ординатой, определяемой
равенством
,
т.е.
,
т.о.,
,
Промежутки знакопостоянства функции:
Т.к. абсциссы точек, лежащих в верхней полуплоскости, положительны, то значения косинуса положительны для углов, расположенных в первой и четвертой координатных четвертях, а значения косинуса отрицательны для углов, расположенных во второй и третьей координатных четвертях.
Т.о.,
при
;
при
;
Интервалы возрастания/убывания
Теорема.
Функция
не является монотонной на всей области
определения, она возрастает на
и убывает на
.
Доказательство:
Докажем,
например, убывание функции на
.
В силу периодичности функции, достаточно
рассмотреть отрезок
.
Для
этого рассмотрим 2 различных значения
,
такие, что
.
Рассмотрим разность значений косинусов этих углов:
(см.
§ 23).
Заметим, что правая часть полученного равенства положительна.
Действительно,
т.к. числа
расположены на отрезке
и
,
то
,
поэтому
;
аналогично
,
поэтому
.
Тем самым доказано, что из неравенства
следует неравенство
,
т.е. функция
убывает на
,
а значит, убывает на каждом из промежутков
вида
.
Аналогичное доказательство возрастания функции на промежутках вида проведите самостоятельно.
График функции.
Г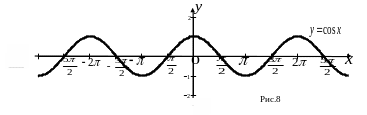
рафик
функции
является синусоидой
(рис. 8).
Свойства функции и её график
О.
Число, равное отношению синуса угла
такого, что
,
к косинусу этого угла
,
называется тангенсом угла
и обозначается
.
Т.к.
каждому значению величины угла
,
кроме
соответствует однозначно определённое
значение
,
то тем самым задана функция
.
Свойства:
Область определения функции: .
Т.к.
и
,
то область определения функции
:
.
Множество значений функции:
Теорема.
Множество
значений функции:
Доказательство:
Действительно,
рассмотрим предел отношения
в точках, не принадлежащих области
определения:
,
.
Во всех остальных точках функция
определена, значит, множество значений
функции:
.
Периодичность:
Теорема.
Наименьший
положительный период функции
равен
Доказательство:
Докажем, что число есть период функции . Применяя формулы приведения, получим следующее:
:
(см. § 19).
Аналогично
(см. § 19)
Докажем, что - наименьший положительный период.
Рассмотрим
значения
,
при которых функция
.
Как известно, дробь равна нулю тогда и
только тогда, когда числитель равен
нулю, а знаменатель не равен нулю. То
есть
.
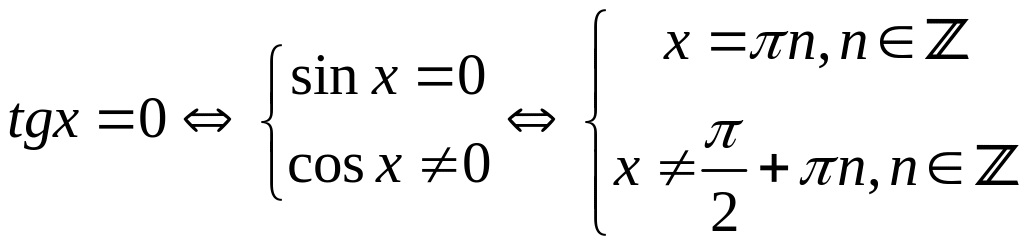Из этого следует, что никакое положительное
число, меньшее
,
не является периодом функции
.
Чётность/нечётность
:
,
таким образом, функция
является нечетной.
Точки пересечения графика с осями координат.
Точки
пересечения с осью
:
Точки
пересечения с осью
:
Промежутки знакопостоянства функции:
Для
тех точек области определения, в которых
синус и косинус имеют одинаковые знаки
.
Для тех точек области определения, в
которых синус и косинус имеют разные
знаки
.
То есть для углов, расположенных в первой и третьей координатных четвертях и - для углов, расположенных во второй и четвертой координатных четвертях.
Т.о.,
при
;
при
.
Интервалы возрастания/убывания
Теорема.
Функция
не является монотонной на всей области
определения, она является возрастающей
на каждом из интервалов вида
.
Доказательство:
Докажем
сначала возрастание функции на
.
Для этого рассмотрим два различных
значения
,
такие, что
..
На рассматриваемом промежутке функция
возрастает, а функция
убывает.
Поэтому
и
,
То
есть
.
Из
и
следует, что
.
Таким образом, функция
возрастает на
.
Аналогично,
докажем возрастание функции на
.
Для
этого рассмотрим два различных значения
,
такие, что
.
На
рассматриваемом промежутке обе функции
и
возрастают, то есть
и
.
Тогда получаем, что
.
,
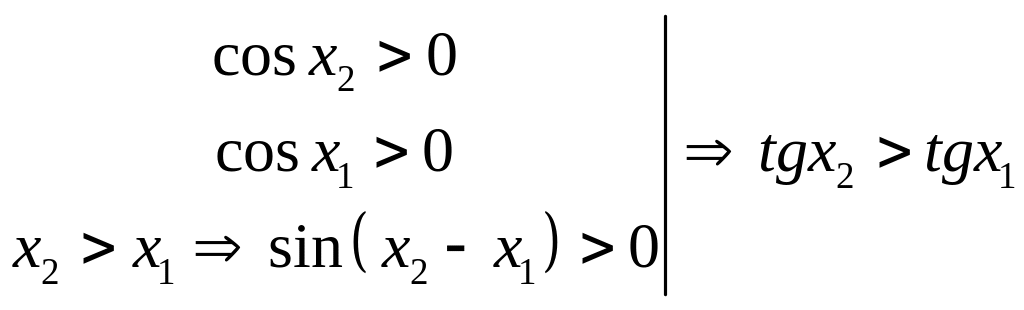а значит, функция
возрастает на
.
Наибольшее/наименьшее значение функции.
Так как множество значений функции: , то функция не имеет ни наибольшего, ни наименьшего значения.
График функции.
График функции имеет вертикальные асимптоты: . (рис. 9)
