Арксинус

О. Функция возрастает на и принимает все значения от до , значит по теореме о корне в промежутке уравнение имеет единственный корень.

Это число называется арксинусом числа и обозначается .

Т.е. арксинусом числа называется такое число из промежутка , синус которого равен : .

Т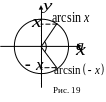 ак как функция на промежутке строго возрастает, значит, по теореме об обратной функции, она имеет обратную функцию: , переобозначив переменные, получаем

Рассмотрим свойства этой функции:

1. Область определения функции:

.

2. Множество значений функции:

3. Периодичность:

Функция не периодическая, так как она строго возрастает на всей области определения (по теореме об обратной функции)

4. Чётность/нечётность

Из рисунка 19 видно, что , т.е. функция нечетная

5. Точки пересечения графика с осями координат.

С осью : если

С осью

6. Промежутки знакопостоянства функции:

:

7. Интервалы возрастания/убывания

П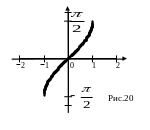 о теореме об обратной функции, так как функция возрастает на ,

следовательно возрастает на .

8. Наибольшее/наименьшее значение функции

Так как функция строго возрастает на всей области определения и непрерывна, то

9. График функции

(рис 20).

Арккосинус

О. Функция возрастает на и принимает все значения от до , значит по теореме о корне в промежутке уравнение имеет единственный корень.

Это число называется арккосинусом числа и обозначается .

Т.е. арккосинусом числа называется такое число из промежутка , косинус которого равен : .

Так как функция на промежутке строго убывает, значит, по теореме об обратной функции, она имеет обратную функцию: , переобозначив переменные, получаем

Рассмотрим свойства этой функции:

1. Область определения функции:

.

2. Множество значений функции:

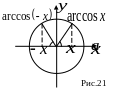
3. Периодичность:

Функция не периодическая, так как она строго убывает на всей области определения (по теореме об обратной функции)

Чётность/нечётность

Из рисунка 21 видно, что , т.е. функция не является ним четной, ни нечетной.

4. Точки пересечения графика с осями координат.

С осью : если

С осью

5. Промежутки знакопостоянства функции:

В силу того, что функция убывает на и , то

6. Интервалы возрастания/убывания

П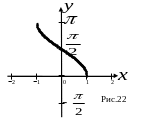 о теореме об обратной функции, так как функция убывает на , следовательно убывает на .

7. Наибольшее/наименьшее значение функции

Так как функция строго возрастает на всей области определения и непрерывна, то

8. График функции

(рис 22).