15. Формула корней квадратного уравнения. Теорема Виета. Формула корней квадратного уравнения.

О. Уравнение вида , где – переменная , называется квадратным.

О. Если , то уравнение называется приведенным квадратным уравнением.

О. Квадратное уравнение, в котором хотя бы один из коэффициентов или равен , называется неполным квадратным уравнением

Выведем формулу корней квадратного уравнения в общем случае:

,

Поделим обе части уравнения на . При этом корни уравнения не изменятся (почему?).

Выделим полный квадрат:

О. Выражение: называется дискриминантом квадратного уравнения, и обозначается через , тогда уравнение можно записать так:

Возможны следующие 3 случая:

1. Если , то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:

или

То есть

или

или

Эти две формулы можно объединить в следующую:

- эта формула называется формулой корней квадратного уравнения

2. Если , то уравнение примет вид:

В этом случае уравнение имеет один корень.

Замечание: можно также сказать, что в этом случае квадратное уравнение имеет два совпадающих корня.

3. Если , то значение дроби , поэтому уравнение , а значит и уравнение не имеет корней (почему?).

Таким образом,

Если , то уравнение имеет 2 различных корня:

Если , то уравнение имеет 2 совпадающих корня:

Если , то уравнение корней не имеет.

Теорема Виета.

Пусть дано уравнение , – корни уравнения, тогда

Доказательство:

Пусть уравнение имеет 2 различных корня ( ):

Итак, действительно

Замечание: Если рассмотреть приведенное квадратное уравнение , то формулы Виета будут выглядеть так: .

В школьном курсе математики чаще всего формулы Виета применяются именно для приведенного квадратного уравнения.

Имеет место теорема, обратная теореме Виета:

Если числа и таковы, что

То эти числа являются корнями уравнения

Доказательство:

Значит, числа и действительно являются корнями уравнения .

Замечание: теорема, обратная теореме Виета, позволяет составлять квадратные уравнения по его корням.

Например, если , то , тогда эти числа являются корнями уравнения

16. Разложение квадратного трехчлена на линейные множители

О. Многочлен вида: , где – переменная , называется квадратным трехчленом.

О. Корнем квадратного трехчлена называется значение переменной, при которой значение этого трехчлена равно нулю.

Теорема.

Если и – корни квадратного трёхчлена , то

Доказательство:

Вынесем за скобки в многочлене множитель а. Получим: . Так как корни квадратного трёхчлена являются корнями квадратного уравнения , то, по теореме Виета, , .

Поэтому

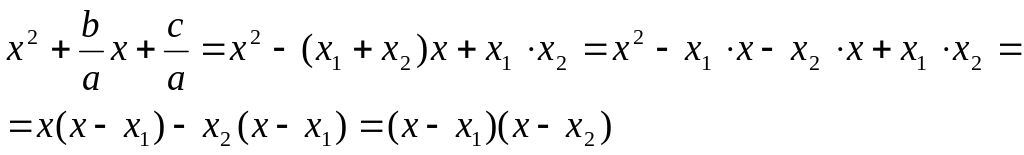
Итак,

Если квадратный трёхчлен имеет один корень (два совпадающих корня), то формула примет вид , где - корень квадратного трёхчлена.

Заметим, что если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.