Практика № 01. Регрессионные модели

Решим на конкретном примере задачу регрессионного анализа, то есть, опираясь на имеющиеся экспериментальные данные, построим модель (определим функцию черного ящика), по которой вход преобразуется в выход (см. рис. П-01.1).

Рис. П-01.1. Схема одномерной регрессионной модели

1Решение задачи регрессионного анализа

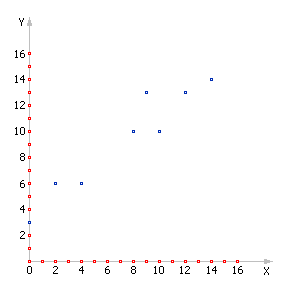
1) Пусть в результате проведения экспериментальных измерений мы получили набор из n = 8 экспериментальных точек. Отобразим их на рис. П-01.2.

Рис. П-01.2. График экспериментальных данных

Занесем полученные данные в табл. П-01.1.

Таблица П-01.1. Экспериментальные данные

i Xi Yi 1 0 3 2 2 6 3 4 6 4 8 10 5 9 13 6 10 10 7 12 13 8 14 14

2) Рассматривая экспериментальные данные, предположим, что они подчиняются линейному закону; выдвигаем гипотезу: Y = aX + b.

3) Запишем уравнение ошибки и суммарной ошибки:

E_i = (Y_i^Эксп. – Y_i^Теор.), i = 1, …, n;

E_i = Y_i – b – aX_i, i = 1, …, n.

4) Для нахождения экстремума приравняем частные производные функции F по переменным b и a к нулю (условие экстремума):

После раскрытия скобок получим систему из двух линейных уравнений:

Для удобства вычислений составим табл. П-01.2.

Таблица П-01.2. Таблица промежуточных вычислений

i Xi Yi Xi2 XiYi 1 0 3 0 0 2 2 6 4 12 3 4 6 16 24 4 8 10 64 80 5 9 13 81 117 6 10 10 100 100 7 12 13 144 156 8 14 14 196 196 Сумма: 59 75 605 685

Для нахождения коэффициентов b и a методом Крамера представим систему в матричной форме:

Подставляя конкретные значения из табл. П-01.2, получим:

Находим значения b и a:

Итак, найденные значения b = 4960/1359 = 3.65 и a = 1055/1359 = 0.78 обеспечивают прохождение графика Y = aX + b как можно ближе одновременно ко всем экспериментальным точкам.

Таким образом, мы получили следующее линейное уравнение: Y = 0.78X + 3.65.

5) Теперь необходимо проверить, имеем ли мы право принять полученную гипотезу Y = 0.78X + 3.65 как верную, или же она должна быть отклонена. Для этого необходимо рассчитать ошибку E_i между точками заданной экспериментальной и полученной теоретической зависимости (см. табл. П-01.3), суммарную ошибку F и значение σ по формулам:

E_i = Y_i – b – aX_i, i = 1, …, n

Таблица П-01.3. Вычисление ошибок между точками заданной экспериментальной и полученной теоретической зависимости

i Xi Yi Ei = Yi – 3.65 – 0.78Xi Ei2 1 0 3 –0.65 0.4225 2 2 6 0.79 0.6241 3 4 6 –0.77 0.5929 4 8 10 0.11 0.0121 5 9 13 2.33 5.4289 6 10 10 –1.45 2.1025 7 12 13 –0.01 0.0001 8 14 14 –0.57 0.3249

Суммарная ошибка составляет:

F = 0.4225 + 0.6241 + 0.5929 + 0.0121 + 5.4289 + 2.1025 + 0.0001 + 0.3249 = 9.5080.

Значение σ = sqrt(9.5080/8) = 1.09. Найдем значение S = σ/cos(arctg(a)) = 1.09/cos(arctg(0.78)) = 1.38.

Если в полосу, ограниченную линиями Y = 0.78X + 3.65 – 1.38 и Y = 0.78X + 3.65 + 1.38 попадет 68.26% или более из всех экспериментальных точек, то можно сделать вывод о том, что наша гипотеза о линейности верна.

Окончательные рассчеты (см. табл. П-01.4) показывают, что 6 точек из 8 (то есть 75%) попадают в полосу, ограниченную линиями Y = 0.78X + 3.65 – 1.38 и Y = 0.78X + 3.65 + 1.38, из чего заключаем: зависимость между входом и выходом модели линейная, то есть выдвинутая нами гипотеза верна.

Таблица П-01.4. Проверка попадания точек внутрь заданного интервала

i Xi Yi Y = 0.78Xi + 3.65 – 1.38 Y = 0.78Xi + 3.65 + 1.38 Есть попадание? 1 0 3 2.27 5.03 Да 2 2 6 3.83 6.59 Да 3 4 6 5.39 8.15 Да 4 8 10 8.51 11.27 Да 5 9 13 9.29 12.05 Нет 6 10 10 10.07 12.83 Нет 7 12 13 11.63 14.39 Да 8 14 14 13.19 15.95 Да

Наконец, дадим графическую иллюстрацию нашим расчетам (рис. П-01.3).

Рис. П-01.3. Найденная линейная зависимость с обозначенным интервалом [–S; +S]

В заключение отметим, что разобранный выше пример — учебный. Поэтому мы ограничились очень небольшим числом экспериментальных точек. В реальных условиях для обеспечения достоверности результатов исследования нужно брать гораздо большее число экспериментальных точек.

Обратно к лекции 02