35. Задача синтеза (обратная задача)

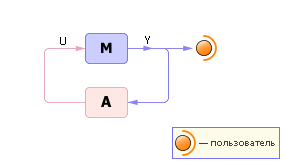
Цель задачи синтеза — нахождение экстремума функции результата. Когда анализ закончен и построены функции, графики, таблицы, когда объект (его свойства и поведение) исследован во всех вариантах возможных входных воздействий, имеет смысл найти среди всего этого многообразия откликов наилучший. Обычно выход — цель функционирования системы, и логично принять, что цель должна принимать лучшие из всех возможных значений, потому имеет смысл найти такие значения входных параметров U, при которых выходной показатель Y примет свое наилучшее значение (экстремум). При этом под экстремумом может подразумеваться как минимум, так и максимум зависимости Y(U). Чтобы найти экстремум, модель включают в контур (см. рис. 20.11) с некоторым алгоритмом A, осуществляющим автоматическое управление входом U и построенным так, что в результате его работы производится поиск такого входного воздействия U на модель M, при котором она выдает наилучший выходной результат.

Рис. 20.11. Схема решения обратных задач (синтез)

Существуют различные алгоритмы поиска оптимума функции Y = M(U). Упомянем три из них (подробно эти и другие методы вы будете изучать в дисциплине «Системный анализ и исследование операций»).

1. Метод перебора. Алгоритм метода перебора представлен на рис. 20.12. Этот метод обеспечивает поиск глобального экстремума, но расточителен к вычислительным ресурсам, так как просматривает все возможные входные значения U с определенным шагом H и выбирает наилучший среди всех выходных результатов Y (см. рис. 20.13). Наилучшее из встреченных Y сохраняется и уточняется в ячейке R, значение U при этом значении Y сохраняется по ходу алгоритма в ячейке Z. Кроме этого имеется риск пропустить нужную точку, «перешагнув» через нее из-за слишком большого размера шага H.

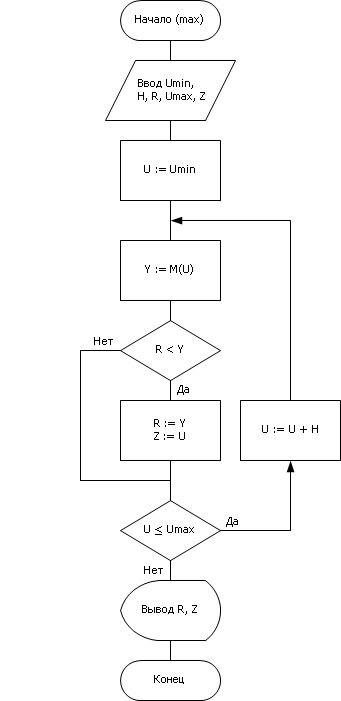
   Рис. 20.12. Алгоритм перебора, примененный к решению задачи синтеза — поиск наилучшего U для максимизации Y

2. Рис. 20.13. Характерный рисунок поиска экстремума функции Y = M(U) методом перебора

3. Метод деления шага пополам. Этот метод более экономичен по отношению к методу перебора, так как анализирует по ходу движения, в каком направлении происходит улучшение (увеличение или уменьшение) функции Y = M(U) и старается двигаться именно в этом направлении. Если при этом попутно обнаруживается, что тенденция во время движения изменилась (уменьшение Y сменилось на его увеличение или наоборот), то алгоритм (рис. 20.14) разворачивается обратно (то есть меняет знак приращения входного сигнала на обратный) и снова идет в нужную сторону, но шаг при этом уменьшается вдвое. Это позволяет подойти к точке экстремума с малым значением шага поиска, что лучше локализует результат (см. рис. 20.15).

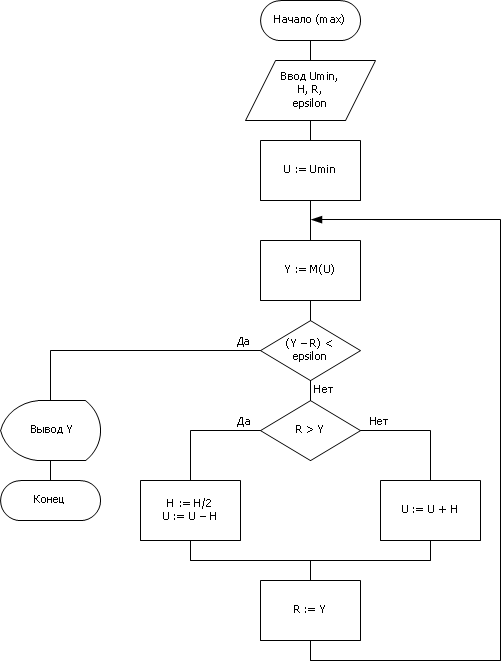
   Рис. 20.14. Алгоритм деления шага пополам, примененный к решению задачи синтеза — поиск наилучшего U для максимизации Y

4. Рис. 20.15. Характерный рисунок поиска экстремума функции Y = M(U) методом деления шага пополам

5. Метод градиента. Метод, алгоритмическая реализация которого представлена на рис. 20.16, использует свойства гипотетической кривой Y = M(U), а именно тот факт, что по направлению производной p, вычисленной на основе двух рядом стоящих точек, можно определить, в какую сторону уменьшается (увеличивается) значение цели Y и двигаться сразу в нужную сторону (см. рис. 20.17). Такая стратегия существенно сокращает время поиска. Недостатком алгоритма является то, что производная может перестать меняться в области локального экстремума, и глобальный экстремум такой алгоритм не найдет.

   Рис. 20.16. Алгоритм поиска экстремума методом градиента, примененный к решению задачи синтеза

Рис. 20.17. Характерный рисунок поиска экстремума функции Y = M(U) методом градиента

Задачу настройки модели мы уже подробно обсуждали в лекциях 02—08 (см. лекцию 02), и останавливаться на ней мы уже не будем. Это способы построения собственно самой модели.